Задачи на движение.
1. Основными компонентами этого типа задач являются:
а) пройденный путь (S);
б) скорость(V);
в) время (t)
Зависимость между указанными величинами выражается известными формулами:
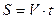
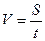
2. План решения обычно сводится к следующему:
а) выбираем одну из величин, которая по условию задачи является неизвестной, и обозначаем ее через x, y или z и т.д.
б) устанавливаем, какая из величин является по условию задачи известной.
в) третью (из оставшихся) величину выражаем через неизвестную (x) и известную с помощью одной из формул.
г) составляем уравнение на основании условия задачи, в котором указано, как именно изменилась (уменьшилась, увеличилась, и т.д.) третья величина.
3. Заметим, что если два каких-либо тела начинают движение одновременно, то в случае, если они встречаются, каждое с момента выхода и до встречи затрачивает, очевидно, одинаковое время. Аналогично обстоит дело и в случае, если одно тело догоняет другое.
4. Если же тела выходят в разное время, то до момента встречи из них затрачивает времени больше то, которое выходит раньше.
5. В задачах на движение по реке необходимо помнить следующие формулы:
Vпо теч=Vсоб+Vтеч
Vпротив теч= Vсоб-Vтеч
Vсоб= 
(Vпо теч+Vпротив теч)
Рассмотрим теперь примерное решение некоторых задач.
Упражнения с решениями.
1. Из пункта А в пункт В, расстояние между которыми равно 18 км, вышел пешеход. Через два часа за ним выехал велосипедист, который проезжал за каждый час на 4,5 км больше, чем проходил пешеход. Определить скорость движения велосипедиста, если известно, что он прибыл в пункт В одновременно с пешеходом.
Решение:
Пусть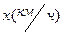 
- V пешехода, тогда (
- V велосипедиста.
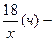время пешехода, тогда 
время велосипедиста.
Зная, что время велосипедиста на 2 часа меньше времени пешехода, составим уравнение:
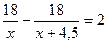ОДЗ: 
приведем к общему знаменателю
2х2 + 9х – 81 = 0
х1,2 = 
(-9 не является решением)
4,5 (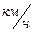
)– V пешехода, тогда V велосипедиста = 4,5 + 4,5 = 9 ()
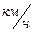Ответ: 4,5; 9
2. Лодочник проезжает расстояние 16 км по течению реки на 6 часов быстрее, чем против течения; при этом скорость лодки в стоячей воде на 2 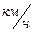больше скорости течения. Определите скорость лодки в стоячей воде и скорость течения реки.
Решение:
Пусть 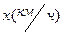- Vсобст, тогда скорость реки 
.
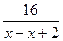- скорость лодки против течения реки.
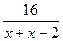- скорость лодки по течению реки.
Зная, что время лодки против течения реки больше времени по течению реки на 6 часов, составим уравнение:
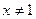
8 -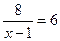 
2х = 10
х = 5 Vсобст= 5 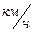, тогда 5 – 2 = 3(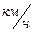)- Vтеч
Ответ: 5;3
Дидактический материал.
1. Моторная лодка прошла 28 км по течению реки и 25км против течения, затратив на весь путь столько же времени, сколько ей понадобилось бы на прохождение 54км в стоячей воде. Определить скорость лодки в стоячей воде, если известно, что скорость течения реки равна 2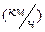 
2. Теплоход должен был пройти 72км с определенной скоростью. Фактически первую половину пути он шел со скоростью на 3 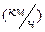меньше и вторую половину со скоростью на 3 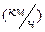больше, чем ему полагалось. На весь путь теплоход затратил 5ч. На сколько минут опоздал теплоход?
3. Моторная лодка шла 40мин по течению реки и 1 час против течения и за это время прошла 37км. Найдите скорость лодки в стоячей воде, если скорость течения реки равна 1,5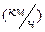
4. Турист проплыл по реке на лодке 90км, а затем прошел пешком 10км. При этом на пеший путь было затрачено на 4ч меньше, чем на путь по реке. Если бы турист шел пешком столько времени, сколько плыл по реке, а плыл по реке столько времени сколько шел пешком, то эти расстояния были бы равны. Сколько времени он шел пешком и сколько плыл по реке?
Задачи на совместную работу.
1. Основными компонентами этого типа задач являются:
а) работа;
б) время;
в) производительность труда(работа, выполненная в единицу времени).
2. План решения задачи обычно сводится к следующему:
а) принимаем всю работу, которую необходимо выполнить, за 1.
б) находим производительность труда каждого рабочего в отдельности, т.е. 
, где t- время, за которое указанный рабочий может выполнить всю работу, работая отдельно.
в) находим ту часть всей работы, которую выполняет каждый рабочий отдельно, за то время, которое он работал.
г) составляем уравнение, приравнивая объем всей работы (т.е. 1) к сумме слагаемых, каждое из которых есть часть всей работы, выполненная отдельно каждым из рабочих (если, разумеется, в условии сказано, что при совместной работе всех рабочих выполнен весь объем работы).
3. Следует заметить, что в указанных задачах не всегда сравнивается выполненная работа. Основанием для составления уравнения может служить также указанное в условии соотношение затраченного времени или производительности труда.
Рассмотрим решение некоторых задач:
Упражнения с решениями.
1. Отец и сын, работая совместно, могут выполнить работу за 2часа 40 минут. Найти время, которое потребуется отцу на выполнение этой работы, если он может выполнить ее на 4 часа бастре сына.
Решение:
Пусть х(ч) – время работы сына, тогда (х – 4)ч – время работы отца.
- производительность труда сына за 1 час, тогда 
-производительность труда отца за 1 час, а 
- производительность труда сына и отца одновременно за 1 час.
Составим уравнение:
ОДЗ: 
3х2 – 28 х + 32 = 0
х1,2 =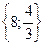 
(
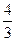не является решением)
8(ч) – время работы сына.
8 – 4 = 4(ч) – время работы отца.
Ответ: 4;8
Дидактический материал.
1. Первый насос наполняет бассейн на 2часа быстрее, чем второй насос выкачивает воду из полного бассейна. За какое время наполняет бассейн первый насос, если при включении обоих насосов бассейн наполняется за 7часов 30минут.
2. Первый тракторист вспахивает поле на 2часа быстрее, чем второй тракторист. Работая вместе, они вспахивают это же поле за 2часа 55минут. За какое время вспахивает это поле первый тракторист?
3. Два портовых крана, работая вместе, разгрузили баржу за 6часов. За какое время может разгрузить баржу, работая отдельно, каждый кран, если одному из них нужно для этого на 9часов меньше, чем другому?
4. Два грузовика, работая вместе, перевозили зерно в течении 4часа. За какое время перевезет то же количество зерна каждый грузовик в отдельности, если первому нужно для этого на 6часов больше, чем второму?
Задачи на планирование.
К задачам этого раздела относятся те задачи, в которых выполняемый объем работы известен или его нужно определить. При этом сравнивается работа, которая должна быть выполнена по плану, и работа, которая выполнена фактически.
Основными компонентами задач на планирование являются:
а) работа (выполненная фактически и запланированная);
б) время выполнения работы (фактическое и запланированное);
в) производительность труда (фактическая и запланированная).
З А М Е Ч А Н И Е: в некоторых задачах этого раздела вместо времени выполнения работы дается количество участвующих в ее выполнении рабочих.
Упражнения с решениями.
1. Две бригады должны были изготовить по 30 деталей. Первая бригада изготовляла в день на 1 деталь больше, поэтому выполнила задание на 1 день раньше второй. Сколько деталей в день изготовляла каждая бригада?
Решение:
Пусть х (д) – в день изготовляла первая бригада, тогда (х + 1)д – в день изготовляла вторая бригада.
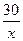- дней выполнила первая бригада, тогда 
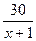- дней выполнила вторая бригада.
Зная, что первая бригада выполнила задание на 1 день раньше второй, составим уравнение:
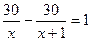
х2 + х – 30 = 0
х1,2 =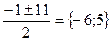 
(-6 не является решением)
5(д) – изготовляла в день первая бригада, тогда 6 деталей в день изготовляла вторая бригада.
Ответ: 5;6
2. Чтобы перевезти груз в 45 т было заказано несколько грузовых машин. Однако с базы прислали другие машины, грузоподъемность которых на 2 т меньше, поэтому пришлось добавить еще 6 машин. Сколько машин перевозили груз?
Решение:
Пусть х(т) – грузоподъемность первых машин, тогда (х – 2)т – грузоподъемность вторых машин.
- количество первых машин, тогда 
- количество вторых машин.
Зная, что вторых машин было на 6 больше, составим уравнение:
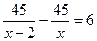
х2 – 2х – 15 = 0
х1,2 =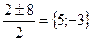 
(-3 не является решением)
5(т) – грузоподъемность первых машин, 5 – 2 = 3(т) – грузоподъемность вторых машин.
= 15 (машин перевозило груз)
Ответ: 15
Дидактический материал.
1. Бригада должна была изготовить 40 деталей к определенному сроку. Изготовляя в час на 3 детали больше, бригада уже за 2 часа до срока изготовила на 8 деталей больше. Сколько деталей в час изготовляла бригада?
2. По плану тракторная бригада должна была вспахать поле за 14 дней. Бригада вспахивала ежедневно на 5 га больше, чем намечалось по плану, и поэтому закончила пахоту за 12 дней. Сколько га было вспахано? Найти площадь поля.
3. Велосипедист должен был проехать весь путь с определенной скоростью за 2 часа. Но он увеличил скорость на 5 км в час, а поэтому на весь путь затратил 1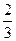 
ч. Найдите длину пути.
4. Заказ по выпуску машин завод должен был выполнить за 20 дней. Но завод выпускал ежедневно по 2 машины сверх плана, а поэтому выполнил заказ за 18 дней. Сколько машин выпустил завод?
