Теория поля
Скалярное и векторное поля
В некоторых профилирующих инженерных дисциплинах (гидромеханика, теплотехника, радиотехника и электротехника) широко используются элементы математической теории поля. Само понятие поля заимствовано из механики и физики. Его смысл заключается в том, что каждой точке пространства или некоторой его области отнесено значение некоторой величины. Поле может быть скалярным или векторным в зависимости от характера рассматриваемой величины. Например, при исследовании неравномерно нагретого твердого тела каждой его точке отнесено значение скалярной величины – температуры и таким образом определено скалярное поле температур. Рассмотрение потока жидкости или газа приводит к векторному полю скоростей частиц жидкости. Другими примерами векторных полей является электрическое поле точечного заряда, гравитационное поле, поле магнитной напряженности и так далее.
При математическом описании поле величины 
определяется функцией переменных 
, 
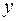и 
:
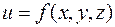(скалярное поле, числовая функция),
(векторное поле).
В случае зависимости от двух переменных поле называют плоским. Понятие нестационарного поля предполагает наличие дополнительной переменной – времени 
: 
.
Рассмотрим скалярное поле, заданное функцией 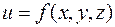. Наглядное представление скалярного поля получается с помощью поверхностей уровня, в точках которых величина принимает постоянное значение и которые имеют уравнения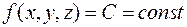 
. Важной характеристикой поля является вектор градиента
. (1)
Вектор 
направлен по нормали к поверхности уровня в сторону наибольшего возрастания функции 
. Через градиент выражается скорость изменения величины в направлении вектора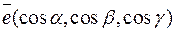 
по формуле
. (2)
Наглядное представление о векторном поле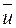 
дают векторные линии, которыми называют кривые, в точках которых касательные направлены в сторону вектора 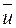. Если 
– радиус-вектор линии, то вектор 
направлен по касательной к ней. Тогда вектор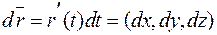 
также направлен по касательной к векторной линии. Это значит (по определению векторной линии), что вектора 
и 
параллельны и поэтому будет
. (3)
Равенства (3) представляют собой систему дифференциальных уравнений и дают возможность определить векторные линии поля.
Пример 1. Скалярное поле 
имеет 
. Для векторного поля градиента из соотношений (3) получим
,
откуда 
или 
;
из уравнения 
находим 
. Таким образом векторное поле имеет векторные линии, которые получаются при пересечении цилиндрических поверхностей плоскостями 
.
Поток векторного поля
Для векторного поля 
произвольной природы интеграл 
называют потоком векторного поля. Поток – величина скалярная. Его наглядный смысл заключается в том, что поток пропорционален числу векторных линий, проходящих через поверхность 
.
Поток выражается через интеграл, который называют поверхностным интегралом второго рода. Вычисление данного интеграла сводится к двойному интегрированию.
Пусть поверхность задана уравнением 
и 
, где 
– проекция поверхности на плоскость ХОУ. В этом случае нормаль к поверхности имеет координаты 
и 
.
, (5)
где .
Примеры. 1. Требуется определить поток векторного поля
через часть плоскости 
, лежащую в первом октанте.
Рис. 6.3. Рис. 6.4.
Из уравнения плоскости находим:
, 
, 
, 
.
Согласно формуле (5) запишем
.
Расстановка пределов интегрирования произведена в соответствии с рисунком 6.3.
2. При вычислении потока векторного поля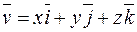 
через поверхность цилиндра, показанного на рис. 6.4, разбиваем интеграл в формуле (6.4) на три части
, (6.6)
где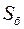 
, 
, 
– соответственно боковая поверхность, верхнее и нижнее основание цилиндра. Так как 
, то скалярное произведение 
равно проекции вектора (радиус-вектор точек поверхности) на направление нормали. Имеем
– для точек боковой поверхности,
– верхнего основания,
– нижнего основания цилиндра.
После подстановки в формулу (6.6) получим
.
Дивергенция векторного поля
Это отношение характеризует среднюю плотность источников или стоков в единице объёма. Его предел при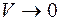 
, когда тело стягивается в точку 
называют дивергенцией векторного поля в точке М
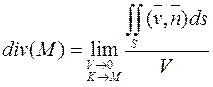. (7)
Таким образом, вводится понятие дивергенции, которое является количественной характеристикой источников и стоков векторного поля.
Установим для дивергенции более удобное выражение чем (7). Для этого воспользуемся формулой Остроградского - Гаусса
, (8)
где 
, V – объём, ограниченный замкнутой поверхностью . С учетом формулы (6.8) получим
. (9)
Выражение (9) позволяет достаточно просто вычислить значение дивергенции, а затем по её знаку определить наличие источников или стоков в точках поля:
- в точке М нет ни источников, ни стоков,
- имеется источник поля,
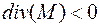- присутствует сток.
