Уравнение выходного звена
Запишем уравнение моментов относительно точки О.
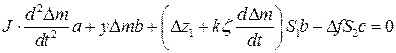
Для перехода к безмерной форме записи введем обозначения:
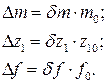
Тогда уравнение запишется в виде:
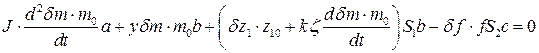
Разделим обе части выражения на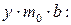 
Обозначим:
Тогда:
3. ПОСТРОЕНИЕ СТРУКТУРНОЙ СХЕМЫ И ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
Уравнения звеньев САР сведем в систему:
выходное звено;
чувствительный элемент;
сервопоршень усилителя первого каскада.
Система уравнений содержит 6 переменных (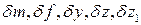
), т. е.,за исключением управляющего воздействия 
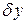и возмущающего воздействия 
, число переменных равно числу уравнений. Систему дифференциальных уравнений записываем в операторной форме:
Изобразим структурную схему выходного звена, описываемого уравнением:
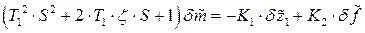
Предварительно 
выразив для упрощения построения: 
Рисунок 3 – Структурная схема выходного звена.
Изобразим структурную схему чувствительного элемента, описываемого уравнением:
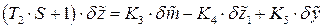
Предварительно 
выразив для упрощения построения:
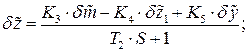
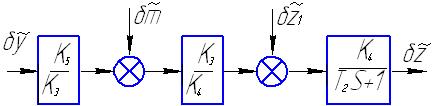
Рисунок 4 – Структурная схема чувствительного элемента.
Изобразим структурную схему сервопоршня, описываемого уравнением:
Предварительно выразим 
для упрощения построения схемы:
Рисунок 5 – Структурная схема сервопоршня.
Изобразив схемы отдельных элементов системы, сгруппируем эти схемы. С помощью такой операции получим структурную схему САР. При группировке учтем, что у нас одно управляющее воздействие 
, и одно возмущающее воздействие 
.
Рисунок 6 – Структурная схема САР.
Рисунок 7 – Структурная схема САР по управляющему воздействию δy.
Для определения передаточной функции САР в разомкнутом состоянии в структурной схеме условно размыкается основная обратная связь и вводятся входной δyвх и выходной δyвых параметры разомкнутой системы. Тогда передаточная функция разомкнутой САР определяется как отношение:
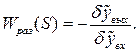
При этом предполагается: 
Выражение для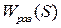 
по управляющему воздействию определяется как произведение:
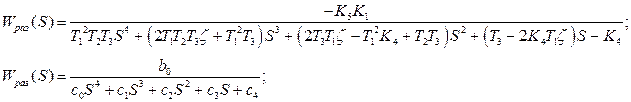
где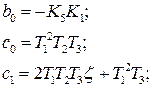 
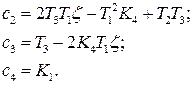
Передаточная функция замкнутой САР по управляющему воздействию δpу,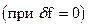 
определяется по формуле:
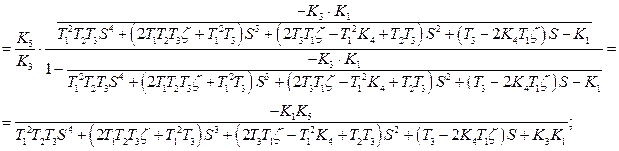
где 
Собственные операторы замкнутой и разомкнутой САР имеют вид:
АНАЛИЗ УСТОЙЧИВОСТИ САР
D-разбиение
Пусть параметром, в плоскости которого строится D-разбиение, является коэффициент К3, который входит в выражение для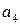 
собственного оператора. Величины остальных коэффициентов считаются заданными. Решается уравнение 
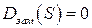или
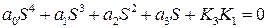относительно коэффициента К3:
Выражение для К3 приводится к стандартной (удобной для подсчета на ЭВМ)форме:
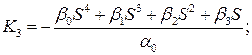
где 
В выражение для коэффициентов уравнения подставляются численные значения параметров САР: 
После подстановки численных значений получаем:
Воспользовавшись программой MathCad определим мнимую и действительную составляющие частотной функции К1 для ряда значений частот. Наибольшую частоту колебаний принимают 
. В результате расчета и построения получим кривую D-разбиения для положительных частот. Зеркальным отображением кривой относительно действительной оси дополняют D-разбиение для отрицательных частот колебаний. Кривая D-разбиения заштриховывается с левой стороны по мере возрастания частоты колебаний ω. Воспользовавшись правилом подсчета корней характеристического уравнения для каждой из выделенных областей D-разбиения, определяют область, соответствующую наибольшему числу корней с отрицательной вещественной частью, т.е. более вероятную область устойчивости САР.
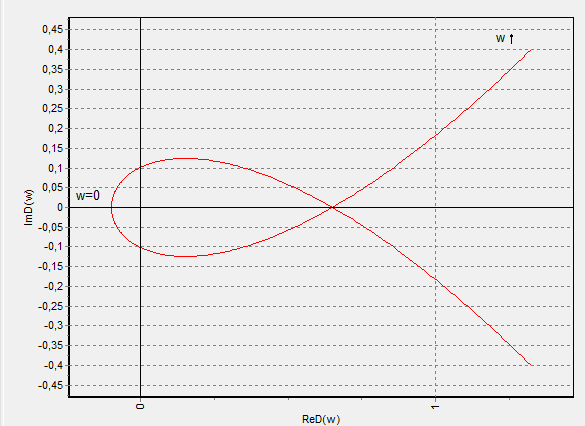
Рисунок 8 – D-разбиение в плоскости коэффициента К1.
Зеркальным отображением кривой относительно действительной оси дополняем кривую D-разбиения для отрицательных частот колебаний. Кривая D-разбиения заштриховывается с левой стороны по мере возрастания частоты колебаний f. Воспользовавшись правилом подсчёта корней характеристического уравнения для каждой из выделенных областей D- разбиения определяем область I, соответствующую наибольшему числу корней с отрицательной вещественной частью, т.е. более вероятную область устойчивости САР.
