Нейромережеве середовище Nntool

Лабораторний практикум

1. Розв¢язок задач нечіткої математики

2. Нечіткі висновки

3. Середовище NNTOOL і його використання для розв¢язку прикладних задач засобами нейромереж

4. Розв¢язок задач апроксимації, прогнозування, класифікації та розпізнавання образів.

1. Засоби MatLab для реалізації операцій нечіткої математики

Мета роботи

1. Опанувати техніку виконання операцій нечіткої математики в середовищі Матлаб.

2. Визначити місце і роль нечіткої математики в загальному контексті штучного інтелекту та інтелектуальних систем.

Порядок виконання роботи

1. Ознайомитись з теоретичним матеріалом з відповідного розділу конспекта лек-цій та методичними вказівками до виконання лабораторної роботи.

2. Підготувати задачу відповідно до варіанта до рівня, доступного для розв¢язання в обраному середовищі (визначити всі потрібні функції, скласти програму).

3. Виконати тестові приклади та визначити особливості власної задачі, зокрема, вплив функції належності та методу дефадзифікації на отриманий результат.

4. Виконати складену в п.2⁰ задачу, дати інтерпретацію отриманим результатам.

Склад звіту

1. Постановка задачі.

2. Програмна документація, підготовлена відповідно до вимог держстандартів України або ЄСПД.

 

 

Тестові приклади та методичні вказівки до виконання лабораторної роботи

Визначення 1. Нечітке число (НЧ) або нечітка змінна (НЗ) на дійсній прямій – це набір, що характеризується функцією належності (ФН) . НЧ(НЗ) можуть бути уявленими у вигляді òm_А(x)/x, дезнак ò вживається як знак об”єднання по всім x є R, m_А(x) є[0,1]- ступінь належності x є R множині .

Визначення 2. Принцип узагальнення. Хай та - НЧ на дійсній прямій R. Тоді арифметичну операцію *_f є (+, -, ´, /) можна представити так:

*_f = òmin(m_А(x), m_B(у))/(x *_f у)

Приклад: арифметичну операцію <приблизно 2> +_f <приблизно 6> згідно до принципа узагальнення можна уявити у такий спосіб

0/0	1/0.5	2/1	3/0.5	4/0
4/0	5/0.0.25	7/0.25	8/0.25	9/0.25		4/0.25
5/0	6/0.5	7/0.5	8/0.5	9/0		5/0.5
6/0	7/0.5	8/1	9/0.5	10/0		6/1
7/0	8/0.5	9/0.5	10/0.5	11/0		7/0.5
8/0	9/0	10/0	11/0	12/0		8/0

 

Результат = {6/0, 7/0.5, 8/1, 9/0.5, 10/0}. Графічне відтворення результату операції наведено нижче.

 

 

Рис. Функції належності, сформовані за допомогою

стандартних засобів MatLab – функія trimf.m

Виклик - TRIMF(X, PARAMS), PARAMS = [A B C] – триелементний вектор A <= B <= C.

Результат арифметичної операції приблизно 2 + приблизно 6, отриманий за допомогою засобів MatLab

Функція MatLab, призначена для реалізації операцій нечіткої математики, наведена нижче

function out = fuzarith(x, A, B, operator)

%FUZARITH Fuzzy arithmetics.

% C = FUZARITH(X, A, B, OPERATOR) returns a fuzzy set C as the result

% of applying OPERATOR on fuzzy sets A and B of universe X. A, B, and X

% should be vectors of the same dimension. OPERATOR should be one of the

% following strings: 'sum', 'sub', 'prod', and 'div'. The returned fuzzy

% set C is a column vector with the same length as A and B. Note that

% This function uses interval arithmetics and it assumes

% 1. A and B are convex fuzzy sets;

% 2. Membership grades of A and B outside of X are zero.

%

% Fuzzy addition could generates "divide by zero" message, but it will

% not affect the correctness of this function. (However, this may cause

% problems on machines without IEEE arithmetic, such as VAX and Cray.)

%

% For example:

x = (0:0.2:14);

A = trimf(x, [0 2 4 ]);

B = trimf(x, [4 6 8]);

C1 = fuzarith(x, A, B, 'sum');

Subplot(2,2,1);

Plot(x, A, x, B, x, C1);

title('fuzzy addition A+B');

Grid on

C2 = fuzarith(x, B, A, 'sub');

Subplot(2,2,2);

Plot(x, A, x, B, x, C2);

title('fuzzy subtraction A-B');

Grid on

C3 = fuzarith(x, A, B, 'prod');

Subplot(2,2,3);

Plot(x, A, x, B, x, C3);

title('fuzzy multiplication A*B');

Grid on

C4 = fuzarith(x, B, A, 'div');

Subplot(2,2,4);

Plot(x, A,x, B, x, C4);

title('fuzzy division A/B');

Grid on

%Roger Jang, 6-23-95

% Copyright (c) 1994-98 by The MathWorks, Inc.

% $Revision: 1.4 $

%Текст програми

x = x(:); A = A(:); B = B(:);

orig_x = x;

% augment x, A, and B for easy interpolation

A = [0; A; 0];

B = [0; B; 0];

x = [min(x)-(max(x)-min(x))/100; x; max(x)+(max(x)-min(x))/100];

tmp = find(diff(A)>0);

index1A = min(tmp):max(tmp)+1; % index for left shoulder

tmp = find(diff(A)<0);

index2A = min(tmp):max(tmp)+1; % index for right shoulder

tmp = find(diff(B)>0);

index1B = min(tmp):max(tmp)+1; % index for left shoulder

tmp = find(diff(B)<0);

index2B = min(tmp):max(tmp)+1; % index for right shoulder

height = linspace(0, 1, 101)';

index1 = find(height > max(A(index1A)));

index2 = find(height > max(A(index2A)));

index3 = find(height > max(B(index1B)));

index4 = find(height > max(B(index2B)));

height([index1; index2; index3; index4]) = [];

leftA = interp1(A(index1A), x(index1A), height, 'linear');

rightA = interp1(A(index2A), x(index2A), height, 'linear');

leftB = interp1(B(index1B), x(index1B), height, 'linear');

rightB = interp1(B(index2B), x(index2B), height, 'linear');

intervalA = [leftA rightA];

intervalB = [leftB rightB];

if strcmp(operator, 'sum'),

% interval mathematics for summation A+B

intervalC = [leftA+leftB rightA+rightB];

х1 = [intervalC(:, 1); flipud(intervalC(:, 2))];

C = [height; flipud(height)];

elseif strcmp(operator, 'sub'),

% interval mathematics for subtraction A-B

intervalC = [leftA-rightB rightA-leftB];

х1 = [intervalC(:, 1); flipud(intervalC(:, 2))];

C = [height; flipud(height)];

elseif strcmp(operator, 'prod'),

% interval mathematics for product A*B

tmp = [leftA.*leftB leftA.*rightB rightA.*leftB rightA.*rightB];

intervalC = [min(tmp')' max(tmp')'];

х1 = [intervalC(:, 1); flipud(intervalC(:, 2))];

C = [height; flipud(height)];

elseif strcmp(operator, 'div'),

% interval mathematics for division A/B

index = (prod(intervalB')>0)'; % contains 0 or not

tmp1 = leftB.*index;

tmp = [leftA./leftB leftA./tmp1 leftA./rightB...

rightA./leftB rightA./tmp1 rightA./rightB];

intervalC = [min(tmp')' max(tmp')'];

х1 = [intervalC(:, 1); flipud(intervalC(:, 2))];

C = [height; flipud(height)];

% get rid of inf or -inf due to division

index = find(~finite(х1));

х1 (index) = [];

C(index) = [];

Else

error('Unknown fuzzy arithmetic operator!');

End

% Make sure that х1 is monotonically increasing

index = find(diff(х1) == 0);

х1 (index) = [];

C(index) = [];

% Take care of "out-of-bound interpolation"

index1 = find(orig_x < min(х1));

index2 = find(orig_x > max(х1));

% tmp_x is legal input for interp1

tmp_x = orig_x;

tmp_x([index1; index2]) = [];

% Do interpolation

out = interp1(х1, C, tmp_x, 'linear');

% Final output

out = [zeros(size(index1)); out; zeros(size(index2))];

 

 

Рис. Результат роботи функції Fuzarith.m: виконання всіх

арифметичних операцій над НЧ (НЗ)

Fuzzy Logic Toolbox включає 11 убудованих функцій належностей, що використовують наступні основні функції:

· кусочно-лінійну;

· гаусовський розподіл;

· сигмоїдну криву;

· квадратичну і кубічні криві.

Для зручності імена всіх убудованих функцій належності закінчуються на mf. Вик-лик функції належності здійснюється в такий спосіб:

Namemf(x, params),

де namemf – найменування функції належності; x – вектор, для координат якого необхідно розрахувати значення функції належності; params – вектор параметрів функції належності.

Найпростіші функції належності трикутна (trimf) і трапецієподібна (trapmf) форму-ється з використанням кусочно-лінійної апроксимації. Трапецієподібна функція належності є узагальнення трикутної, вона дозволяє задавати ядро нечіткої множини у вигляді інтерва-лу. У випадку трапецієподібної функції належності можлива наступна зручна інтерпрета-ція: ядро нечіткої множини – оптимістична оцінка; носій нечіткої множини – песимістична оцінка.

Дві функції належності – симетрична гаусівська (gaussmf) і двостороння гаусівська (gaussmf) формується з використанням гаусівського розподілу. Функція gaussmf дозволяє задавати асиметричні функція належності. Узагальнена дзвоноподібна функція належності (gbellmf) за своєю формою схожа на гаусівські. Ці функції належності часто використовую-ться в нечітких системах, тому що на всій області визначення вони є гладкими і приймають ненульові значення.

Функції належності sigmf, dsigmf, psigmf засновані на використанні сигмоидної кри-вої. Ці функції дозволяють формувати функції належності, значення яких починаючи з дея-кого значення аргументу і до + (-) рівні 1. Такі функції зручні для завдання лінгвістичних термов типу “високий” чи “низький”.

Поліноміальна апроксимація застосовується при формуванні функцій zmf, pimf і smf, графічні зображення яких схожі на функції sigmf, dsigmf, psigmf, відповідно.

Основна інформація про убудовані функції належності зведена в табл. 6.1. На рис. 6.1 приведені графічні зображення функцій належності, отримані за допомогою демон-страційною сценарію mfdemo. Як видно з малюнка, убудовані функції належності дозво-ляють задавати різноманітні нечіткімножини.

У Fuzzy Logic Toolbox передбачена можливість для користувача створення власної функції належності. Для цього необхідно створити m-функцію, що містить два вхідних аргументи – вектор, для координат якого необхідно розрахувати значення функції належності і вектор параметрів функції належності. Вихідним аргументом функції повинний бути вектор ступенів належності. Нижче приведена m-функція, що реалізує дзвоноподібну функцію належності :

function mu=bellmf(x, params)
%bellmf – bell membership function;
%x – input vector;
%params(1) – concentration coefficient (>0);
%params(2) – coordinate of maximuma.
a=params(1);
b=params(2);
mu=1./(1+ ((x-b)/a).^2);

Рис. 6.1. Убудовані функції належності

Таблиця 6.1. Функції належності

Назва функції	Опис	Аналітична формула
dsigmf	функція належности у вигляді різниці між двома сигмоїд-ними функціями
gauss2mf	двостороння гаусівська функція належності	якщо c1<c2, то ; якщо c1>c2, то .

 

gaussmf	симетрична гаусівська функція належності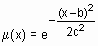
gbellmf	узагальнена дзвоноподібна функція принадлежности
pimf	пі-подібна функці належності	добуток smf та zmf функцій
psigmf	добуток двох сигмоїдних функцій належності
sigmf	сигмоїдна функція належносіи
smf	s-подібна функція належності
trapmf	трапецієвидна функція належності
trimf	трикутна функцфія належності
zmf	z-подібна функція належності

 

Порядок параметров	№ функції належності
[a1 c1 a2 c2]
[c b]
[a b c]
[a b c d] [a d] – носій нечіткої множини; [b c] – ядро нечіткої множини;
[a1 c1 a2 c2]
[a c]
[a, b]
[a, b, c, d]
[a, b, c]
[a, b]

Варіанти завдань

 

Використовуючи стандартні засоби Fuzzy Logic Toolbox MatLab, скласти программу для обчислення алгебраїчного виразу, який складається з нечітких змінних: ;

№ варіанту	Значення змінних і тип ФН	Метод дефадзифікації результaту
	Приблизно 10- gaussmf	Приблизно 7- trapmf	Приблизно 4- trimf	centroid
	Приблизно 11- trimf	Приблизно 10- gaussmf	Приблизно 7- trapmf	bisector
	Приблизно 10- трик	Приблизно 10- gaussmf	Приблизно 10- trapmf	centroid
	Приблизно 10- gaussmf	Приблизно 10- gaussmf	Приблизно 10- gaussmf	bisector
	Приблизно 10- trapmf	Приблизно 10- trapmf	Приблизно 10- trapmf	centroid
	Приблизно 10- грикут	Приблизно 15- gaussmf	Приблизно 11- trimf	bisector
	Приблизно 10- trapmf	Приблизно 10- trimf	Приблизно 10- trimf	centroid
	Приблизно 10- трик	Приблизно 10- gaussmf	Приблизно 10- trapmf	centroid
	Приблизно 10- gaussmf	Приблизно 10- gaussmf	Приблизно 10- gaussmf	bisector

 

Нечіткі висновки

Проектування систем типу Мамдані

Мета роботи

1. Опанувати техніку виконання операцій нечітких висновків в середовищі Матлаб.

2. Визначити місце і роль нечіткої логіки в загальному контексті штучного інтелекту та інтелектуальних систем.

Порядок виконання роботи

1. Ознайомитись з теоретичним матеріалом з відповідного розділу конспекта лек-цій та методичними вказівками до виконання лабораторної роботи.

2. Підготувати задачу відповідно до варіанта до рівня, доступного для розв¢язання в обраному середовищі (визначити всі потрібні функції, скласти програму).

3. Виконати тестові приклади та визначити особливості власної задачі, зокрема, вплив функції належності та методу дефадзифікації на отриманий результат.

4. Виконати складену в п.2⁰ задачу, дати інтерпретацію отриманим результатам.

Склад звіту

1. Постановка задачі.

2.Програмна документація, підготовлена відповідно до вимог держстандартів України або ЄСПД.

 

Тестові приклади та методичні вказівки до виконання лаборпторної роботи

Розглянемо роботу системи нечіткого логічного висновку пакета Fuzzy Logic Toolbox на прикладі проектування систем типу Мамдани, виконавши моделювання (представлення, аппркосимація) залежності , 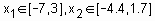. Проектування системи нечіткого логічного висновку, а саме створення бази знань – системи правил, доцільно проводити на основі графічного зображення зазначеної залежності. Для побудови тривимірного зображення функції в області створимо наступну програму:

 

%Побудова графіка функції y= х1 ^2*sin(x2-1)

%

%в області x1є[-7,3] і x2є[-4.4,1.7].
n=15;
х1 =-7:10/(n-1):3;
x2=-4.4:6.1/(n-1):1.7;
y=zeros(n,n);
for j=1:n
y(j,:)= х1. ^2*sin(x2(j)-1);
end
surf(х1,x2,y)
xlabel(' х1 ')
ylabel('x2')
zlabel('у')
title('Target');

 

У результаті виконання програми одержимо графічне зображення, приведене на рис. 3.1. Інтерактивний процес проектування системи нечіткого логічного висновку, що відповідає приведеному графіку, складається у виконанні наступної послідовності кроків.

Рис.3.1. Еталонна поверхня

1⁰. З авантажити основний fis-редактор - використовують команду fuzzy у команд-ному рядку. Після цього відкриється нове графічне вікно, показане на рис. 3.2.

 

 

Рис.3.2. Вікно редактора FIS-Editor

2⁰. Робота з вхідними змінними: починаємо з введення другої вхідної змінної, для цього в меню Edit вибираємо команду Add input.

3⁰. Першу вхідну змінну перейменуємо. Для цього зробимо один щиглик лівою кнопкою миші на блоці input1, введемо нове позначення х1 у поле редагування імені поточної змінної і натиснемо <Enter>.

4⁰. Відповідно перейменуємо другу вхідну змінну. Для цього зробимо один щиглик лівою кнопкою миші на блоці input2, введемо нове позначення x2 у поле редагування імені поточної змінної і натиснемо <Enter>.

5⁰. Робота з вихідною змінною. Перейменуємо вихідну змінну. Для цього зробимо один щиглик лівою кнопкою миші на блоці output1, введемо нове позначення y у поле редагування імені поточної змінної і натиснемо <Enter>.

60. Задамо ім'я системи. Для цього в меню File вибираємо в підменю Export команду To disk і вводимо ім'я файлу, наприклад, first.

7⁰. Перейдемо в редактор функцій належності. Для цього зробимо подвійного щиглика лівою кнопкою миші на блоці х1.

8⁰. Задамо діапазон зміни змінної х1. Для цього введемо значення діапазону і надрукуємо -7 3 у поле Range (див. рис. 3.3) і натиснемо <Enter>.

9⁰. Задамо функції належності змінної х1. Для лінгвістичної оцінки цієї змінної будемо використовувати 3 терма з трикутними функціями належності. Для цього в меню Edit виберемо команду Add MFs... У результаті з'явитися діалогове вікно вибору типу і кількості функцій належностей. За замовчуванням це 3 терма з трикутними функціями належності. Тому просто натискаємо <Enter>.

10⁰. Задамо найменування термов змінної х1. Для цього робимо один щиглик лівою кнопкою миші за графіком першої функції належності (див. рис. 3.3). Потім вводимо найменування терма, наприклад, Низький, у поле Name і натиснемо <Enter>. Потім робимо один щиглик лівою кнопкою миші за графіком другої функції належності і вводимо найменування терма, наприклад, Середній, у поле Name і натиснемо <Enter>. Ще раз робимо один щиглик лівою кнопкою миші за графіком третьої функції належності і вводимо найменування терма, наприклад, Високий, у поле Name і натиснемо <Enter>. У результаті одержимо графічне вікно, зображене на рис. 3.3.

Рис.3.3. Функції належності змінної х1

11⁰. Задамо функції належності змінної x2. Для лінгвістичної оцінки цієї змінної будемо використовувати 5 термів з гаусовськими функціями належності. Для цього активізуємо змінну x2 за допомогою щиглика лівої кнопки миші на блоці x2. Задамо діапазон зміни змінної x2. Для цього надрукуємо -4.4 1.7 у полі Range (див. рис. 3.4) і натиснемо <Enter>. Потім у меню Edit виберемо команду Add MFs.... У діалоговому вікні, що з¢явилось, вибираємо тип функції належності gaussmf у полі MF type і 5 термів у полі Number of MFs. Після цього натискаємо <Enter>.

Рис 3.4. Функції належності змінної x2

12⁰. За аналогією з кроком 10 задамо наступні найменування термов змінної x2: Низький, Нижче середнього, Середній, Вище за середнє, Високий. У результаті одержимо графічне вікно, зображене на рис. 3.4.

13⁰. Задамо функції належності змінної y. Для лінгвістичної оцінки цієї змінної будемо використовувати 5 термів із трикутними функціями належності. Для цього активізуємо змінну y за допомогою щиглика лівої кнопки миші на блоці y. Задамо діапазон зміни змінної y. Для цього надрукуємо -50 50 у полі Range (див. рис. 3.5) і натиснемо <Enter>. Потім у меню Edit виберемо команду Add MFs.... У діалоговому вікні, що з¢яіилось, вибираємо 5 термів у полі Number of MFs. Після цього натискаємо <Enter>.

Рис 3.5. Функції належності змінної y

14⁰. За аналогією з кроком 10 задамо наступні найменування термов змінної y: Низький, Нижче середнього, Середній, Вище за середнє, Високий. У результаті одержимо графічне вікно, зображене на рис. 3.5.

15⁰. Перейдемо в редактор бази знань RuleEditor. Для цього виберемо в меню Edit виберемо команду Edit rules....

16⁰. На основі візуального спостереження за графіком, зображеним на рис. 3.1 сформулюємо наступні дев'ять правил:

1. Якщо х1 =Середній, то y =Середній;

2. Якщо х1 =Низький і х2 =Низький, то у =Високий;

3. Якщо х1 =Низький і х2 =Високий, то у =Високий;

4. Якщо х1 =Високий і х2 =Високий, то у =Вище За середнє;

5. Якщо х1 =Високий і х2 =Низький, то у =Вище За середнє;

6. Якщо х1 =Високий і х2 =Середній, то у =Середній;

7. Якщо х1 =Низький і х2 =Середній, то у =Низький;

8. Якщо х1 =Високий і х2 =Вище За середнє, то у =Середній;

9. Якщо х1 =Високий і х2 =Нижче Середнього, то у =Середній.

Для введення правила необхідно вибрати в меню відповідну комбінацію термов і натиснути кнопку Add rule. На рис. 3.6 зображене вікно редактора бази знань після введення всіх дев'яти правил. Число, приведене в дужках наприкінці кожного правила являє собою ваговий коефіцієнт відповідного правила.

Рис 3.6. База знань у RuleEditor

17⁰. Збережемо створену систему. Для цього в меню File вибираємо в підменю Export команду To disk.

На рис. 3.7 приведене вікно візуалізації нечіткого логічного висновку. Це вікно активізується командою View rules... меню View. У полі Input наводяться значення вхідних змінних, для яких виконується логічний висновок.

Рис 3.7. Візуалізація нечіткого логічного висновку в RuleViewer

На рис. 3.8 приведена поверхня “вхід-вихід”, що відповідає синтезованій нечіткій системі. Для висновку цього вікна необхідно використовувати команду View surface... меню View. Порівнюючи поверхні на рис. 3.1 і на рис. 3.8 можна зробити висновок, що нечіткі правила досить добре описують складну нелінійну залежність.

.

Рис 3.8. Поверхня “вхід-вихід” у вікні SurfaceViwer

 

 

Виконати моделювання (апроксимація) функціональної залежності на підставі систем нечіткого висновку типу Мамдані:

- шляхом використання графічного інтерфейсу;

- шляхом створення окремої програми

 

Варіанти завдань

 

№ варіанту	Тип функції	Область визначення змінних	Примітки
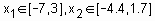
	y=F (x 1, x 2) = sin(x 1 + x 2) – x 1	x 1, x 2 [0, 2pi]
	y= F (x 1, x 2)=exp(– x 1)+ sin(x 2/2)	x 1, x 2 [0, 2pi]
	y=F (x 1, x 2, x 3) = sin(x 1 + x 2 + x 3)	x 1, x 2, x 3 [0, 2pi/3]
	y=F (x 1, x 2, x 3) = cos(x 1 + x 2 + x 3)	x 1, x 2, x 3 [0, 2pi/3]
	y=F (x 1, x 2, x 3) = sin((x 1+ x 2 + x 3)/2)	x 1, x 2, x 3 [0, 2pi/3]
	y=F (x 1, x 2, x 3) = cos((x 1+ x 2 + x 3)/2)	x 1, x 2, x 3 [0, 2pi/3]
	y=F (x 1, x 2, x 3) = exp(– x 1) + exp(– x 2) + exp(x 3/2)	x 1, x 2, x 3 [0, 2pi/3]
	y=F (x 1, x 2, x 3) = sin(x 1 + x 2 + x 3)	x 1, x 2, x 3 [0, 2pi/3]

 

Нейромережеве середовище Nntool

(графічний інтерфейс користувача)

 

Мета роботи

1. Опанувати техніку розв¢язання задач в середовищі нейромереж - Nntool.

2. Визначити місце і роль штучних нейромереж в загальному контексті штучного інтелекту та інтелектуальних систем.

Порядок виконання роботи

1. Ознайомитись з теоретичним матеріалом з відповідного розділу конспекта лек-цій та методичними вказівками до виконання лабораторної роботи.

2. Підготувати задачу відповідно до варіанта до рівня, доступного для розв¢язання в обраному середовищі (визначити всі потрібні функції).

3. Виконати тестові приклади та визначити особливості власної задачі, зокрема, вплив початкового наближеного розв¢язку на отриманий результат, вплив кількості нейронів та шарів.

4. Виконати складену в п.2⁰ задачу, дати інтерпретацію отриманим результатам.

Склад звіту

1. Постановка задачі.

2. Екранні форми, які розкривають сутність задачі та параметри нейромережі.

 

Тестові приклади та методичні вказівки до виконання лабораторної роботи

Нейронні мережі (NN - Neural Networks) широко використовуються для рішення різноманітних задач. Серед областей застосування, що розвиваються,

- обробка аналогових і цифрових сигналів, синтез і ідентифікація електронних ланцюгів і систем. Основи теорії і технології застосування НМе широко представлені в пакеті MATLAB. У цьому зв'язку особливо слід зазначити останню версію пакета - MATLAB 6.0, де вперше представлений засіб GUI (Graphical User Interface - графічний інтерфейс користувача) для НМе - NNTool.

Прикладами застосування технології нейронних мереж для цифрової обробки сигналів є: фільтрація, оцінка параметрів, детектування, ідентифікація систем, розпізнавання образів, реконструкція сигналів, аналіз часових рядів і стиск. Згадані види обробки застосовні до різноманітних видів сигналів: звукових, відео, мовних, зображень, передачі повідомлень, геофізичних, локаційних, медичних вимірів (кардіограми, енцефаллограми, пульс) і т.ін.

У даному посібнику дано опис NNTool і показана техніка його застосування для рішення реальних прикладних задач, зокрема, задач цифрової обробки сигналів, що є найбільш показовим для фахівця з комп'ютерної інженерії.

Після того як структура НМе обрана, повинні бути встановлені її параметри. Вибір структури НМе і типів нейронів - самостійний і дуже непросте питання, що тут ми обговорювати не будемо. Що ж стосується значень параметрів, то, як правило, вони визначаються в процесі рішення деякої оптимізаційної задачі. Ця процедура в теорії НМе називається навчанням.

Графічний інтерфейс користувача NNTool дозволяє вибирати структури НМе із великого переліку і надає множина алгоритмів навчання для кожного типу мережі. В учбово-методичному посібнику розглянуті наступні питання, що відносяться до роботи з NNTool:

· призначення графічних керуючих елементів;

· підготовка даних;

· створення нейронної мережі;

· навчання мережі;

· прогін мережі.

Всі етапи роботи з мережами проілюстровані прикладами рішення простих задач.

Керуючі елементи NNTool

Щоб запустити NNTool, необхідно виконати одноїменну команду в командному вікні MATLAB:

>> nntool

після цього з'явиться головне вікно NNTool, іменоване "Вікном керування мережами і даними" (Network/Data Manager) (рис. 1).

Рис. 1. Головне вікно NNTool

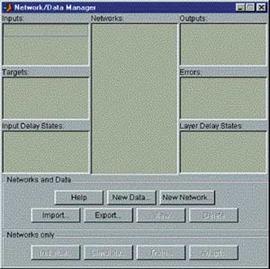
Панель "Мережі і дані" (Networks and Data) має функціональні клавіші з наступними призначеннями:

· Допомога (Help)- короткий опис керуючих елементів даного вікна;

· Нові дані (New Data...)- виклик вікна, що дозволяє створювати нові набори даних;

· Нова мережа (New Network...)- виклик вікна створення нової мережі;

· Імпорт (Import...)- імпорт даних з робочого простору MATLAB у простір змінних NNTool;

· Експорт (Export...)- експорт даних із простору змінних NNTool у робочий простір MATLAB;

· Вид (View)- графічне відображення архітектури обраної мережі;

· Видалити (Delete)- видалення обраного об'єкта.

На панелі "Тільки мережі" (Networks only) розташовані клавіші для роботи винятково з мережами. При виборі покажчиком миші об'єкта будь-якого іншого типу, ці кнопки стають неактивними. При роботі з NNTool важливо пам'ятати, що клавіші View, Delete, Initialize, Simulate, Train і Adapt (зображені на рис. 1 як неактивні) діють стосовно до того об'єкта, що відзначений у даний момент виділенням. Якщо такого об'єкта немає, або над виділеним об'єктом неможливо зробити зазначену дію, відповідна клавіша неактивна.

Розглянемо створення нейронної мережі за допомогою NNTool на прикладі.

Приклад 1.

Нехай потрібно створити нейронну мережа, що виконує логічну функцію "І".

Створення мережі

Виберемо мережу, що складається з одного персептрона з двома входами. У процесі навчання мережі на її входи подаються вхідні дані і виробляється зіставлення значення, отриманого на виході, з цільовим (бажаним). На підставі результату порівняння (відхилення отриманого значення від бажаного) обчислюються величини і змінні ваг і зсуву, що зменшують це відхилення.

Перед створенням мережі необхідно заготовити набір навчальних і цільових даних. Складемо таблицю істинності для логічної функції "І", де P1 і Р2 - входи, а А - бажаний вихід (табл. 1).

Табл. 1. Таблиця істинності логічної функції "І"

P1	P2	A

Щоб задати матрицю, що складається з чотирьох векторів-рядків, як вхідну, скористаємося кнопкою New Data. У вікні, що з'явилося, варто зробити змінними, показані рис. 2, і натиснути клавішу "Створити" (Create).

Рис. 2. Завдання вхідних векторів

Рис. 3. Завдання цільового вектора

 

Після цього у вікні керування з'явиться вектор data1 у розділі Inputs. Вектор цілей задається аналогічно (рис. 3).

Після натискання на Create у розділі Targets з'явиться вектор target1. Дані в поле "Значення" (Value) можуть бути представлені будь-яким зрозумілим MATLAB виразом. Приміром, що визначення вектора цілей можна еквівалентно замінити рядком виду

bitand([0 0 1 1], [0 1 0 1]).

Тепер варто приступити до створення нейронної мережі. Вибираємо кнопку New Network і заповнюємо форму, як показано на рис. 4.

При цьому поля несуть наступні значеннєві навантаження:

· Ім'я мережі (Network Name) - це ім'я об'єкта створюваної мережі.

· Тип мережі (Network Type)- визначає тип мережі й у контексті обраного типу представляє для введення різні параметри в частині вікна, розташованої нижче цього пункту. Таким чином, для різних типів мереж вікно змінює свій зміст.

· Вхідні діапазони (Input ranges)- матриця з числом рядків, рівним числу входів мережі. Кожен рядок являє собою вектор із двома елементами: перший - мінімальне значення сигналу, що буде подано на відповідний вхід мережі при навчанні, другий - максимальне. Для спрощення введення цих значень передбачений список, що випадає, "Одержати з входу" (Get from input), що дозволяє автоматично сформувати необхідні дані, вказавши ім'я вхідної змінної.

· Кількість нейронів (Number of neurons)- число нейронів у шарі.

· Передатна функція (Transfer function)- у цьому пункті вибирається передатна функція (функція активації) нейронів.

· Функція навчання (Learning function)- функція, що відповідає за відновлення ваг і зсувів мережі в процесі навчання.

Рис. 4. Вікно "Створення мережі"

Рис. 5. Попередній перегляд створюваної мережі

 

За допомогою клавіші "Вид" (View) можна подивитися архітектуру створюваної мережі (рис. 5).Так, ми маємо можливість упевнитися, чи всієї дії були зроблені вірно. На рис. 5 зображена персептронная мережа з вихідним блоком, що реалізує передатну функцію з твердим обмеженням. Кількість нейронів у шарі дорівнює одному, що символічно відображається розмірністю вектора-стовпця на виході шару і вказується числом безпосередньо під блоком передатної функції. Розглянута мережа має два входи, тому що розмірність вхідного вектора-стовпця дорівнює двом.

Отже, структура мережі відповідає нашому завданню. Тепер можна закрити вікно попереднього перегляду, натиснувши клавішу "Закрити" (Close), і підтвердити намір створити мережу, натиснувши "Створити" (Create) у вікні створення мережі.

У результаті пророблених операцій у розділі "Мережі" (Networks) головного вікна NNTool з'явиться об'єкт з ім'ям network1.

Навчання

Наша мета - побудувати нейронну мережу, що виконує функцію логічного «І». Очевидно, не можна розраховувати на те, що відразу після етапу створення мережі остання буде забезпечувати правильний результат (правильне співвід-ношення "вхід/вихід"). Для досягнення мети мережу необхідно належним образом навчити, тобто підібрати придатні значення параметрів. У MATLAB реалізована більшість відомих алгоритмів навчання нейронних мереж, серед яких представлене два для персептронних мереж розглянутого виду. Створюючи мережу, ми вказали LEARNP як функцію, що реалізує алгоритм навчання (рис. 4).

Повернемося в головне вікно NNTool. На даному етапі інтерес представляє нижня панель "Тільки мережі" (Networks only). Натискання кожної з клавіш на цій панелі викликає вікно, на множині вкладок якого представлені параметри мережі, необхідні для її навчання і прогону, а також відбивають поточний стан мережі.

Відзначивши покажчиком миші об'єкт мережі network1, викличемо вікно керування мережею натисканням кнопки Train. Перед нами виникне вкладка "Train" вікна властивостей мережі, що містить, у свою чергу, ще одну панель вкладок (рис. 6).Їхнє головне призначення - керування процесом навчання. На вкладці "Інформація навчання" (Training info) потрібно вказати набір навчальних даних у поле "Входи" (Inputs) і набір цільових даних у поле "Мети" (Targets). Поля "Виходи" (Outputs) і "Помилки" (Errors) NNTool заповнює автоматично. При цьому результати навчання, до яких відносяться виходи і помилки, будуть зберігатися у змінних із зазначеними іменами.

Рис. 6. Вікно параметрів мережі, відкрите на вкладці "навчання" (Train)

Рис. 7. Вкладка параметрів навчання

 

Завершити процес навчання можна, керуючись різними критеріями. Можливі ситуації, коли переважно зупинити навчання, думаючи достатнім деякий інтервал часу. З іншого боку, об'єктивним критерієм є рівень помилки.

На вкладці "Параметри навчання" (Training parameters) для нашої мережі (рис. 7)можна установити наступні поля:

· Кількість епох (epochs)- визначає число епох (інтервал часу), по закінченню якого навчання буде припинено.

· Епохою називають однократне представлення всіх навчальних вхідних даних на входи мережі.

· Досягнення мети (goal)- тут задається абсолютна величина функції помилки, при якій ціль буде вважатися досягнутою.

· Період відновлення (show)- період відновлення графіка кривої навчання, виражений числом епох.

· Час навчання (time)- після закінчення зазначеного тут часового інтервалу, вираженого в секундах, навчання припиняється.

Приймаючи в увагу той факт, що для задач з лінійно віддільними множинами (а наша задача відноситься до цього класу) завжди існує точне рішення, установимо порог досягнення мети таким, що дорівнює нулю. Значення інших параметрів залишимо за замовчуванням. Помітимо тільки, що поле часу навчання містить запис Inf, що визначає нескінченний інтервал часу (від англійського Infinite - нескінченний).

Наступна вкладка "Необов'язкова інформація" (Optional Info) показана на рис. 8.

Рис.8.Вкладка необов'язкової інформації

Рис. 9. Крива навчання

 

Розглянемо вкладку навчання (Train). Щоб почати навчання, потрібно натиснути кнопку "Навчити мережа" (Train Network). Після цього, якщо в даний момент мережа не задовольняє жодній з умов, зазначених у розділі параметрів навчання (Training Parameters), з'явиться вікно, що ілюструє динаміку цільової функції - криву навчання. У нашому випадку графік може виглядати так, як показано на рис. 9. Кнопкою "Зупинити навчання" (Stop Training) можна припинити цей процес. З малюнка видно, що навчання було зупинено, коли функція мети досягла установленої величини (goal = 0).

Слід зазначити, що для персептронов, що мають функцію активації з твердим обмеженням, помилка розраховується як різниця між метою й отриманим виходом.

Отже, алгоритм навчання знайшов точне рішення задачі. У методичних цілях переконаємося в правильності рішення задачі шляхом прогону навченої мережі. Для цього необхідно відкрити вкладку "Прогін" (Simulate) і вибрати в списку, що випадають, "Входи" (Inputs) заготовлені дані. У даній задачі природно використовувати той же набір даних, що і при навчанні data1. При бажанні можна установити прапорець "Задати мети" (Supply Targets). Тоді в результаті прогону додатково будуть розраховані значення помилки. Натискання кнопки "Прогін мережі" (Simulate Network) запише результати прогону в змінну, ім'я якої зазначено в полі "Виходи" (Outputs). Тепер можна повернутися в основне вікно NNTool і, виділивши мишею вихідну змінну network1, натиснути кнопку "Перегляд" (View). Вміст вікна перегляду збігається зі значенням вектора цілей - мережа працює правильно.

Варто помітити, що мережа створюється ініціалізованою, тобто значення ваг і зсувів задаються певним чином. Перед кожним наступним досвідом навчання звичайно початкові умови обновляються, для чого на вкладці "Ініціалі-зація" (Initialize) передбачена функція ініціалізації. Так, якщо потрібно провести кілька незалежних досвідів навчання, ініціалізація ваг і зсувів перед кожним з них здійснюється натисканням кнопки "Ініціалізувать ваги" (Initialize Weights).

Повернемося до вкладки "Необов'язкова інформація" (Optional Info) (рис. 8).Щоб зрозуміти, якої мети служать представлені тут параметри, необхідно обговорити два поняття: перенавчання й узагальнення.

При виборі нейронної мережі для рішення конкретної задачі важко передбачити її порядок. Якщо вибрати невиправдано великий порядок, мережа може виявитися занадто гнучкою і може представити просту залежність складним образом. Це явище називається перенавчанням. У випадку мережі з недостатньою кількістю нейронів, навпроти, необхідний рівень помилки ніколи не буде досягнутий. Тут у наявності надмірне узагальнення.

Для попередження перенавчання застосовується наступна техніка. Дані поділяються на дві множині: навчальну (Training Data) і контрольну (Validation Data). Контрольна множина у навчанні не використовується. На початку роботи помилки мережі на навчальномій і контрольній множинаах будуть однаковими. У міру того, як мережа навчається, помилка навчання убуває, і, поки навчання зменшує дійсну функцію помилки, помилка на контрольній множині також буде убувати. Якщо ж контрольна помилка перестала убувати чи навіть стала рости, це вказує на те, що навчання варто закінчити. Зупинка на цьому етапі називається ранньою зупинкою (Early stopping).

Таким чином, необхідно провести серію експериментів з різними мережами, перш ніж буде отримана придатна. При цьому щоб не бути введеним в оману локальними мінімумами функції помилки, слід кілька разів навчати кожну мережу.

Якщо в результаті послідовних кроків навчання і контролю помилка залишається неприпустимо великою, доцільно змінить модель нейронної мережі (наприклад, ускладнити мережу, збільшивши число нейронів, чи використовувати мережа іншого виду). У такій ситуації рекомендується застосовувати ще одну множину - тестова множина спостережень (Test Data), що являє собою незалежну вибірку з вхідних даних. Підсумкова модель тестується на цій множині, що дає додаткову можливість переконатися у вірогідності отриманих результатів. Очевидно, щоб зіграти свою роль, тестова множина повинна бути використано тільки один раз. Якщо її використовувати для коригування мережі, вона фактично перетвориться в контрольну множинуа.

Установка верхнього прапорця (рис. 8) дозволить задати контрольну множина і відповідний вектор цілей (можливо, той же, що при навчанні). Установка нижнього дозволяє задати тестову множина і вектор цілей для нього.

Навчання мережі можна проводити в різних режимах. У зв'язку з цим, у NNTool передбачено дві вкладки, що представляють навчальні функції: розглянута раніше вкладка Train і "Адаптація" (Adapt). Adapt уміщає вкладку інформація адаптації (Adaption Info), на якій містяться поля, схожі по своєму призначенню з полями вкладки Training Info і виконують ті ж функції і вкладку параметри адаптації (Adaption Parameters). Остання містить єдине поле "Проходи" (passes). Значення, зазначене в цьому полі, визначає, скільки разів усі вхідні вектори будуть представлені мережі в процесі навчання.

Параметри вкладок "Train" і "Adapt" у MATLAB використовуються функ-ціями train і adapt, відповідно. Докладна довідкова інформація з цих функцій приведена в у HELP-файлі.

Поділ лінійно-невіддільних множин

Розглянута задача синтезу логічного елемента «І» може трактуватися як задача розпізнавання лінійно віддільних множин. На практиці ж частіше зустрі-чаються задачі поділу лінійно невіддільних множин, коли застосування персептронов з функцією активації з твердим обмеженням не дасть рішення. У таких випадках варто використовувати інші функції активації.

Показовим прикладом лінійно невіддільної задачі є створення нейронної мережі, що виконує логічну функцію " виключаюче ЧИ".

Приклад 2.

Нехай потрібно створити нейронну мережа, що виконує логічну функцію " виключаюче ЧИ".

Розглянемо таблицю істинності цієї функції (табл. 2).

Таблиця 2. Таблиця істинності логічної функції " виключаєче ЧИ"

P1	P2	A

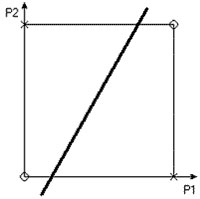
Що ж мається на увазі під "лінійною невіддільністю" множин? Щоб відповісти на це питання, зобразимо множина вихідних значень у просторі входів (рис. 10),випливаючи наступному правилу: сполучення входів P1 і P2, при яких вихід A звертається в нуль, позначаються кружком, а ті, при яких A звертається в одиницю - хрестиком.

Наша мета - провести границю, що відокремлює множину нулів від множини хрестиків. З побудованої картини на рис. 10 видно, що неможливо провести пряму лінію, яка б відокремила нулі від одиниць. Саме в цьому змісті множина нулів лінійно невіддільно від множині одиниць, і персептрони, розглянуті раніше, у принципі, не можуть вирішити розглянуту задачу.

Якщо ж використовувати персептроны зі спеціальними нелінійними функ-ціями активації, наприклад, сигмоідними, то рішення задачі можливо.

Рис. 10. Стан логічного елемента " виключаюче ЧИ"

Рис. 11. Мережа для рішення задачі " виключаюче ЧИ"

 

Виберемо персептрон з двома нейронами схованого шару, у яких функції активації сигмоїдні, і одним вихідним нейроном з лінійною функцією активації (рис. 11).Як функцію помилки вкажемо MSE (Mean Square Error - середній квадрат помилки). Нагадаємо, що функція помилки встановлюється у вікні "Створення мережі" після вибору типу мережі.

Ініціалізуємо мережу, натиснувши кнопку Initialize Weights на вкладці Initialize, після чого навчимо, указавши як вхідні значення сформовану раніше змінну data1, як мету - новий вектор, що відповідає бажаним виходам. У процесі навчання мережа не може забезпечити точного рішення, тобто звести помилку до нуля. Однак виходить наближення, яке можна спостерігати по кривій навчання на рис. 12.

Слід зазначити, що дана крива може змінювати свою форму від експерименту до експерименту, але, у випадку успішного навчання, характер функції буде монотонно убутним. У результаті навчання, помилка була мінімізована до дуже малого значення, що практично можна вважати рівним нулю.

Задача синтезу елемента " виключаюче ЧИ" є також прикладом задачі класифікації. Вона відбиває загальний підхід до рішення подібного роду задач.

 

 

Рис. 12. Крива навчання в задачі " щовиключає ЧИ"

Рис. 13. Архітектура мережі для рішення задачі апроксимації

Задача апроксимації

Однією з головних властивостей нейронних мереж є здатність апроксимувати і, більш того, бути універсальними апроксиматорами. Сказане означає, що за допомогою нейронних ланцюгів можна апроксимувати як завгодно точно неперервні функції багатьох змінних. Розглянемо приклад.

Приклад 3.

Необхідно виконати апроксимацію функції наступного виду

де x € 1?N, а N - число крапок функції.

Заготовимо цільові дані, ввівши в поле "Значення" (Value) вікна створення нових даних вираз:

sin(5*pi*[1:100]/100+sin(7*pi*[1:100]/100)).

Ця крива являє собою відрізок періодичного коливання з частотою 5p/N, модульованого по фазі гармонійним коливанням з частотою 7 N (рис. 15).

Тепер заготовимо набір навчальних даних (1, 2, 3,..., 100), задавши їх наступним виразом:

1:100.

Рис. 14. Крива навчання в задачі апроксимації

Рис. 15. Червона крива - цільові дані, синя крива - апроксимуюча функція

 

Виберемо персептрон (Feed-Forward Back Propagation) з тринадцятьма сигмоиїниыми (TANSIG) нейронами схованого шару й одним лінійним (PURELIN) нейроном вихідного шару. Навчання будемо робити, використовуючи алгоритм Левенберга-Маркардта (Levenberg-Mar-quardt), що реалізує функція TRAINLM. Функція помилки - MSE. Отримана мережа має вид, зображений на рис. 13.

Тепер можна приступити до навчання. Для цього необхідно вказати, які набори даних повинні бути використані в якості навчальних і цільових, а потім провести навчання (рис. 14).

Рис. 15 ілюструє різницю між цільовими даними й отриманою апроксимуючою кривою. З рис. 14 і 15 видно, наскільки зменшилася помилка апроксимації за 100 епох навчання. Форма кривої навчання на останніх епохах говорить також про те, що точність наближення може бути підвищена.

Розпізнавання образів

Однієї з областей застосування нейронних мереж є розпізнавання образів. Апроксимаційні можливості НМе грають тут першорядну роль.

Приклад 4.

Необхідно побудувати і навчити нейронну мережу для рішення задачі розпізнавання цифр. Ціль цього приклада - показати загальний підхід до рішення задач розпізнавання образів. Тому, щоб не захаращувати виклад технічними деталями, позначимо лише ключові моменти, думаючи, що на даному етапі читач готовий самостійно зробити відповідні дії з NNTool.

Система, що має бути синтезувати за допомогою нейронної мережі, буде навчена сприймати символи, близькі до шаблонового (рис. 16).

Рис. 16. Монохромне зображення вихідних даних

Рис. 17. Графічне представлення масиву вихідних даних

 

Набори вихідних даних (не плутати з цільовими даними) можна як завантажувати з файлів зображень, так і створювати безпосередньо в MATLAB. Рис. 17 ілюструє вміст масиву вихідних даних. Одержимо навчальні дані, наклавши шум на набір вихідних даних (рис. 18).

Рис. 18. Навчальні дані

Рис. 19. Вікно імпорту і завантаження даних з MAT-файлу

У задачах класифікації, до яких відноситься даний приклад, кількість виходів мережі відповідає числу поділюваних мережею класів. Цей факт повинний бути врахований при виборі архітектури мережі і на етапі формування цільових даних. Мережа класифікації дає найбільше значення на виході, що відповідає придатному класу. При добре сконструйованій і навченій НМе значення інших виходів будуть помітно менше.

Для рішення цієї задачі обрана мережа Feed-forward backprop з п'ятьма сигмоїдними нейронами першого шару і п'ятьма лінійними нейронами другого шару. Алгоритм навчання - Левенберга-Маркардта. З такою конфігурацією мережа після восьми епох навчання дала помилку порядку 10^-30.

Щоб упевнитися в правдивості результату, ми прогнали мережу на заготовленій контрольній множині. Мережа бездоганно розділила і нову вибірку зашумленних символів.

Завершуючи приклад, відзначимо, що вже зараз успішно розробляються різномані