Расчётно-аналитическая часть.
Задание 1.
По семи цехам завода имеются данные о расходовании материала на производство продукции. Определить расход материала на 1 изделие в среднем по заводу.
| Номер цеха | Расход материала, м | Номер цеха | Расход материала, м | ||
| На одно изделие | На все изделия | На одно изделие | На все изделия | ||
| 0,6 | 0,5 | ||||
| 0,7 | 1,5 | ||||
| 0,9 | 0,25 | ||||
| 0,4 |
Решение:
Средний расход на 1 изделие = 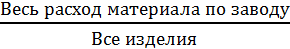
Средний расход на 1 изделие = 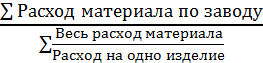
Средний расход на 1 изделие = 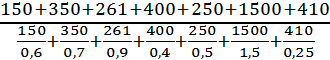 = =
= = 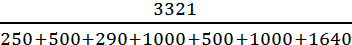 =
= 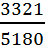 = 0,64 (м/изд.)
= 0,64 (м/изд.)
Ответ: средний расход материала на одно изделие 0,64 м.
Задание 2.
Выработка ткани по цехам фабрики характеризуется следующими показателями:
| Номер цеха | Базисный период | Отчётный период | ||
| Численность рабочих, чел. | Средняя выработка за смену одним рабочим, м | Выработка ткани всего, м | Средняя выработка за смену одним рабочим, м | |
Определите среднюю выработку ткани по заводу за смену одним рабочим:
1) в базисном периоде,
2) в отчётном периоде.
Сравните полученные данные. Укажите, какие виды средних необходимо применить в каждом случае.
Решение:
1) в базисном периоде:
Применяем среднюю взвешенную:
Средняя выработка по = 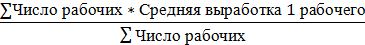
заводу 1 рабочим
Средняя выработка по = 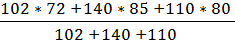 =
=
заводу 1 рабочим
= 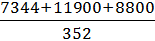 =
= 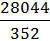 = 76,67 (м.)
= 76,67 (м.)
Ответ: в базисном периоде 1 рабочий за смену вырабатывает в среднем по заводу 76,67 м. ткани.
2) в отчётном периоде:
Применяем среднюю гармоническую:
Средняя выработка по = 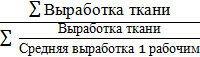
заводу 1 рабочим
Средняя выработка по = 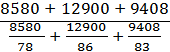 =
= 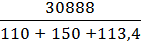 =
= 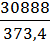
заводу 1 рабочим
= 82,72 (м.)
Ответ: в отчётном периоде 1 рабочий за смену вырабатывает в среднем по заводу 82,72 м. ткани.
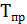 =
= 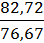 * 100 % – 100 % = 8 %.
* 100 % – 100 % = 8 %.
Вывод: средняя выработка ткани по заводу одним рабочим за смену в отчётном году по сравнению с базисным увеличилась на 8 %.
Задание 3.
Имеются следующие данные о снижении себестоимости по отдельным видам продукции в отчётном периоде по сравнению с базисным периодом и о сумме затрат в производстве в отчётном периоде.
| Вид продукции | Снижение себестоимости, % | Сумма затрат в производстве в отчётном периоде, млн.руб. |
| 5,5 | ||
| 10,1 | ||
| 20,3 | ||
| 15,5 | ||
| 18,3 |
Вычислить, на сколько в среднем произошло снижение себестоимости по всем видам продукции.
Решение:
Вычислим индекс себестоимости по каждому виду продукции:
ic (1) = 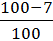 = 0,93;
= 0,93;
ic (2) = 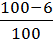 = 0,94;
= 0,94;
ic (3) = 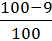 = 0,91;
= 0,91;
ic (4) = 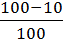 = 0,9;
= 0,9;
ic (5) = 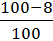 = 0,92.
= 0,92.
Ic = 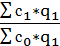 ; ic =
; ic = 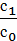 , => с0 =
, => с0 = 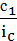 ,
,
где с1 – себестоимость в отчётном периоде,
с0 – себестоимость в базисном периоде.
Получим:
Ic = 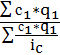
Ic = 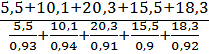 =
= 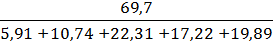 =
= 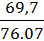 =
=
= 0,916.
Тпр = Ic * 100 % – 100 % = 0,916 * 100 % – 100 % = – 8,4 %.
Вывод: в отчётном периоде по сравнению с базисным себестоимость по всем видам продукции снизилась в среднем на 8,4 %.
Задание 4.
Имеются следующие данные о работе 24-х заводов одной отрасли промышленности
| № завода п/п | Среднегодовая стоимость основных производственных фондов, млн. руб. | Производство продукции за отчетный год, млн. руб. |
| 6,4 | ||
| 9,5 | ||
| 19,2 | ||
| 18,8 | ||
| 13,4 | ||
| 6,7 | ||
| 12,8 | ||
| 7,5 | ||
| 4,6 | ||
| 2,7 | ||
| 6,5 | ||
| 15,8 | ||
| 7,2 | ||
| 7,5 | ||
| 25,8 | ||
| 11,2 | ||
| 8,8 | ||
| 4,6 | ||
| 23,8 | ||
| 18,8 |
По данным таблицы выполнить группировку с равными интервалами заводов по среднегодовой стоимости ОПФ.
Для определения числа групп воспользоваться формулой Стерджесса. Построить вариационный интервальный ряд. Построить полигон, гистограмму, кумуляту. Найти среднее значение изучаемого признака. Найти структурные средние: моду и медиану (с помощью приближённых формул и по гистограмме и кумуляте). Вычислить показатели вариации: размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Объяснить смысл каждого показателя.
Решение:
Определим, на сколько групп нужно разбить совокупность по формуле Стерджесса:
k = 1 + 3,322 * lg N,
где N – объём совокупности.
k = 1 + 3,322 * lg 24 = 1 + 3,322 * 1,38 = 1 + 4,58 = 5,58 ≈ 6 групп.
Длина одной части диапазона колебаний:
h = 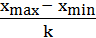
h = 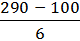 = 31,67 =32
= 31,67 =32







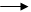




99 131 163 195 227 259 291
 |
диапазон колебаний
Интервальная группировка с равными интервалами:
| № группы | Среднегодовая стоимость | Частости предела |
| I | [99; 131) | |
| II | (131; 163] | |
| III | (163; 195] | |
| IV | (195; 227] | |
| V | (227; 259 ] | |
| VI | (259; 291] |
Вариационный интервальный ряд:
| Номер группы | Среднегодовая стоимость | xi – середина интервала | mi – частота | wi – частости | Fi – накопленные частоты | Pi – накопленные частости |
| I | [99; 131) | 0,21 | 0,21 | |||
| II | (131; 163] | 0,21 | 0,42 | |||
| III | (163; 195] | 0,21 | 0,62 | |||
| IV | (195; 227] | 0,25 | 0,87 | |||
| V | (227; 259] | 0,08 | 0,96 | |||
| VI | (259; 291] | 0,04 | ||||
| Итого: | N = 24 |
Середина интервала:
x1 = 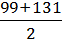 = 115;
= 115;
x2 = 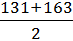 = 147;
= 147;
x3 = 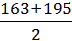 = 179;
= 179;
x4 = 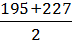 = 211;
= 211;
x5 = 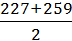 = 243;
= 243;
x6 = 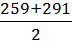 = 275.
= 275.
Частости:
w1 = 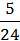 = 0,21;
= 0,21;
w2 = 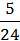 = 0,21;
= 0,21;
w3= 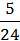 = 0,21;
= 0,21;
w4 = 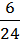 = 0,25;
= 0,25;
w5 = 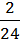 = 0,08;
= 0,08;
w6 = 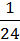 = 0,04.
= 0,04.
Накопленные частоты:
F1 = 5;
F2 = 5 + 5 = 10;
F3 = 10 + 5 = 15;
F4 = 15 + 6 = 21;
F5 = 21 + 2 =23;
F6 = 23 + 1 = 24.
Накопленные частости:
Pi = 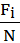
P1 = 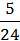 = 0,21;
= 0,21;
P2 = 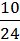 = 0,42;
= 0,42;
P3 = 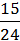 = 0,62;
= 0,62;
P4 = 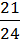 = 0,87;
= 0,87;
P5 = 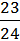 = 0,96;
= 0,96;
P6 = 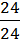 = 1.
= 1.
Полигон частот.
Гистограмма.
Кумулята.
Находим среднегодовую стоимость ОПФ одного завода:
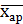 =
= 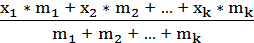 ,
,
где k – число групп;
xk – значение середины интервалов;
mk – соответствующие частоты.
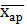 =
= 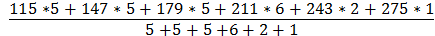 =
=
= 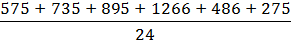 =
= 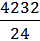 =
=
= 176,3
Мода.
Определение моды с помощью приближённой формулы:
Мо ≈ xo + h * 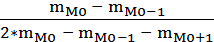 ,
,
где xo – нижняя граница модального интервала;
h – длина модального интервала;
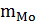 – частота модального интервала;
– частота модального интервала;
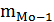 – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному;
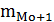 – частота интервала, следующего за модальным.
– частота интервала, следующего за модальным.
xo = 195;
h = 32;
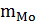 = 6;
= 6;
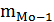 = 5;
= 5;
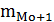 = 2.
= 2.
Мо = 195 + 32 * 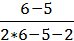 = 201,4.
= 201,4.
Медиана.
Определение медианы с помощью приближённой формулы:
Ме ≈ xo + h * 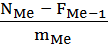 ,
,
где xo – нижняя граница медианного интервала;
h – длина медианного интервала;
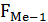 – накопленная частота интервала, предшествующего медианному;
– накопленная частота интервала, предшествующего медианному;
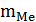 – частота медианного интервала;
– частота медианного интервала;
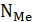 – номер медианы
– номер медианы
(Если N – чётное, 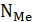 =
= 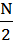 ;
;
если N – нечётное, 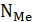 =
= 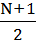 ,
,
где N – объём совокупности).
N = 24 – чётное число, => 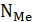 =
= 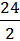 = 12.
= 12.
12 – ему соответствует интервал (163; 195];
xo = 163;
h = 32;
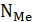 = 12;
= 12;
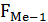 = 10;
= 10;
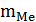 = 5.
= 5.
Ме ≈ 163 + 32 * 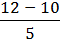 = 175,8
= 175,8
Дисперсия.
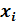
| ||||||
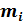
| ||||||
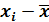
| -61,3 | -29,3 | 2,7 | 34,7 | 66,7 | 98,7 |
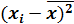
| 3757,69 | 858,49 | 7,29 | 1204,09 | 4448,89 | 9741,69 |
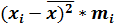
| 18788,45 | 4292,45 | 36,45 | 7224,54 | 8897,78 | 9741,69 |
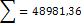
Д = 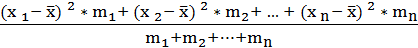 ,
,
где xi – конкретное значение признака;
mi – частота;
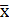 – среднее значение.
– среднее значение.
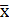 = 185,7
= 185,7
Д = 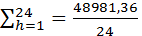 = 2040,89
= 2040,89
Среднее квадратическое отклонение.
σ = 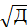
σ = 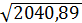 = 45,18
= 45,18
Коэффициент вариации.
V =  * 100 %
* 100 %
V = 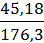 * 100 % = 25,63 %.
* 100 % = 25,63 %.
Задание 5.
Имеются следующие данные о выпуске продукции прядильного производства за 5 лет
| Год | |||||
| Пряжа, тонн |
Рассчитать все показатели динамики (базисный год – 2008): средний уровень ряда, абсолютные изменения – приросты или сокращения (цепные и базисные), коэффициенты и темпы роста (цепные и базисные), темпы прироста (цепные и базисные), абсолютное значение 1 % прироста, средний абсолютный прирост (сокращение).
Решение:
Средний уровень ряда:
Данный ряд является моментным (на определённую дату) с равными промежутками между датами. Средний уровень ряда найдём по формуле средней арифметической простой:
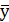 =
= 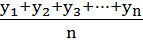
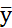 =
= 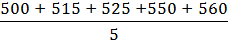 =
= 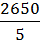 = 530 т.
= 530 т.
Ответ: средний ежегодный выпуск пряжи составил 530т.
Абсолютные изменения (приросты или сокращения):
а) цепные:
∆yц = yt – yt-1
∆yц = 515 – 500 = +15;
∆yц = 525 – 515 = +10;
∆yц = 550 – 525 = + 25;
∆yц = 560 – 550 = + 10.
б) базисные:
∆yбаз = yt – yо
∆yбаз = 515 – 500 = + 15;
∆yбаз = 525 – 500 = + 25;
∆yбаз = 550 – 500 = + 50;
∆yбаз = 560 – 500 = + 60.
Коэффициенты динамики:
а) цепные:
i дин.цепной = 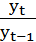
i дин.цепной = 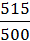 = 1,03;
= 1,03;
i дин.цепной = 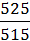 = 1,019;
= 1,019;
i дин.цепной = 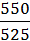 = 1,048;
= 1,048;
i дин.цепной = 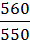 = 1,018.
= 1,018.
б) базисные:
i дин.баз. = 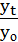
i дин.баз. = 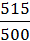 = 1,03;
= 1,03;
i дин.баз. = 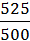 = 1,05;
= 1,05;
i дин.баз. = 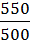 = 1,1;
= 1,1;
i дин.баз. = 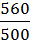 = 1,12.
= 1,12.
Темпы роста:
а) цепные:
Т рцепной = i дин.цепной * 100 %
Т рцепной = 1,03 * 100 % = 103%;
Т рцепной = 1,019 * 100 % = 101,9 %;
Т рцепной = 1,048 * 100 % = 104,8%;
Т рцепной = 1,018* 100 % = 101,8%.
б) базисные:
Т рбаз = i дин.баз * 100 %
Т рбаз = 1,03 * 100 % = 103%;
Т рбаз = 1,05 * 100 % = 105%;
Т рбаз = 1,1 * 100 % = 110%;
Т рбаз = 1,12 * 100 % = 112%.
Темпы прироста:
а) цепные:
Т прцепной = Т рцепной – 100 %
Т прцепной = 103% – 100 % = + 3 %;
Т прцепной = 101,9 % – 100 % = + 1,9 %;
Т прцепной = 104,8% – 100 % = + 4,8 %;
Т прцепной = 101,8% – 100 % = + 1,8 %.
б) базисные:
Т прбаз = Т рбаз – 100 %
Т прбаз = 103% – 100 % = + 3 %;
Т прбаз = 105% – 100 % = + 5 %;
Т прбаз = 110 % – 100 % = + 10 %;
Т прбаз = 112 % – 100 % = + 12 %.
Абсолютное значение 1 % прироста:
α = 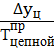
α = 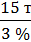 ≈ 5 т;
≈ 5 т;
α = 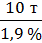 ≈ 5,26 т;
≈ 5,26 т;
α = 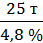 ≈ 5,21 т;
≈ 5,21 т;
α = 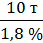 ≈ 5,55 т.
≈ 5,55 т.
| yо баз | |||||
| Год | |||||
| yt – выпуск пряжи, т | |||||
| ∆yц, т | – | + 15 | +10 | + 25 | + 10 |
| ∆yбаз, т | – | + 15 | + 25 | + 50 | + 60 |
| i дин.цепной | – | ≈ 1,03 | ≈ 1,019 | ≈ 1,048 | ≈ 1,018 |
| i дин.баз | – | ≈ 1,03 | ≈ 1,05 | ≈ 1,1 | ≈ 1,12 |
| Т рцепной | – | 103% | 101,9 % | 104,8% | 101,8% |
| Т рбаз | – | 103% | 105% | 110 % | 112% |
| Т прцепной | – | + 3 % | + 1,9 % | + 4,8 % | + 1,8 % |
| Т прбаз | – | + 3 % | + 5 % | + 10 % | + 12 % |
| α | – | ≈ 5 | ≈ 5,26 | ≈ 5,21 | ≈ 5,55 |
Средний абсолютный прирост (сокращение):
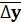 =
= 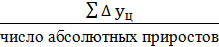
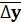 =
= 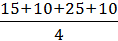 = 16,25 (т.)
= 16,25 (т.)
Ответ: среднее ежегодное увеличение выпуска пряжи составило 16,25 тонн.






