Основы статической обработки экспериментальных данных. Часть 1.
В-7
Цель работы: Ознакомиться с методами статической обработки результатов испытания или обследования строительных конструкций.
Задачи:
1. Освоить процедуру нахождения закона распределения случайной величины.
2. Освоить процедуру построения парной зависимости по экспериментальным данным.
3. Научиться производить оценку статической значимости полученных зависимостей и распределений.
1) Математическое ожидание:
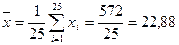
2) Среднеквадратичное отклонение:
3) Проверка совместимости данных:
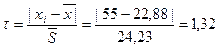≤2,72
(грубых ошибок нет)
4) Количество интервалов.
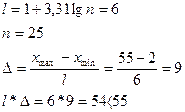
Условие не выполняется, следовательно l принимается равным 7
l=9*7=63
Таким образом, выборка разбивается на 7 интервалов с шагом ∆=9мм
Выборка:
| № | x(f) | (x-ˉх)² |
| 435,9744 | ||
| 1622,478 | ||
| 1465,358 | ||
| 1316,238 | ||
| 1244,678 | ||
| 1041,998 | ||
| 916,8784 | ||
| 857,3184 | ||
| 799,7584 | ||
| 744,1984 | ||
| 690,6384 | ||
| 589,5184 | ||
| 541,9584 | ||
| 411,2784 | ||
| 334,1584 | ||
| 265,0384 | ||
| 233,4784 | ||
| 176,3584 | ||
| 105,6784 | ||
| 68,5584 | ||
| 39,4384 | ||
| 27,8784 | ||
| 0,0784 | ||
| 22,2784 | ||
| 137,3584 |
Затем, после полученных данных вычисляем характеристики х²в и заносим в следующую таблицу.
| № | серед. интер | nk | Распределение Гаусса | Распределение Лапласа | ||||||
| ρk | pk | npk | ((nk-npk)^2) /npk | ρk | pk | npk | ((nk-npk)^2) /npk | |||
| 4,5 | 0,0126361 | 0,113725 | 2,843125 | 1,636265516 | 0,004772716 | 0,042954 | 1,073861 | |||
| 13,5 | 0,0230516 | 0,207464 | 5,1866 | 0,12756339 | 0,011969172 | 0,107723 | 2,693064 | 18,41 | ||
| 22,5 | 0,0271811 | 0,24463 | 6,115738 | 0,203552069 | 0,021450998 | 0,193059 | 4,826475 | 0,0062 | ||
| 31,5 | 0,0227948 | 0,205153 | 5,128828 | 0,248449134 | 0,011883018 | 0,106947 | 2,673679 | 4,46 | ||
| 40,5 | 0,0141713 | 0,127542 | 3,188548 | 0,556 | 0,005492894 | 0,049436 | 1,235901 | |||
| 49,5 | 0,0060157 | 0,054142 | 1,353538 | 0,002338967 | 0,021051 | 0,526268 | ||||
| 58,5 | 0,0022772 | 0,020495 | 0,512364 | 0,001173681 | 0,010563 | 0,264078 |
При этом необходимо выполнение условия npk»2. Если в некоторых интервалах это условие не выполняется, то они объединяются с соседними.
Гаусса:
- теоретическая вероятность попадания случайной величины в к -ый интервал.
Лапласа:
а) Гаусса
х²в=2,77< 
б) Лапласа
х²в=22,9˃ 
Вывод: Сравнение характеристик х²в с теоретическими значениями показывают, что данная выборка может быть удовлетворительно описана для з-на Гаусса, а для з-на Лапласса не удовлетворяется, т.к. не выполняется неравенство.
Оценка парных зависимостей. Часть 2.
Другой задачей статистической обработки эмпирических данных является отыскание зависимости между двумя случайными величинами, одна из которых выступает в качестве аргумента, другая является функцией отклика. Эта задача решается с помощью линейного парного регрессионного анализа, в основу которого положен метод наименьших квадратов. Согласно этому методу линия регрессии, связывающая две случайные величины, строится так, чтобы сумма квадратов отклонений вдоль оси ординат была минимальной:
, (1)
где 
- экспериментальное значение функции в точке i.
- теоретическое значение функции в той же точке.
Теоретическая линия регрессии может быть линейной
Или носить более сложный характер. Задача сводится к отысканию коэффициентов регрессии a, b, что достигается путем вычисления частных производных функции (1) по параметрам a, b и получения системы нормальных уравнений.
Парный регрессионный анализ осуществляется в следующем порядке:
а) принимается уравнение линии регрессии;
б) вычисляется необходимые суммы для решения системы нормальных уравнений;
в) вычисляются коэффициенты регрессии;
г) определяется значение общей дисперсии
,
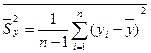где n – число экспериментальных точек;
- среднее значение функции.
;
д) определяется значение остаточной дисперсии
; (2)
е) вычисляется отношение дисперсий и сравнивается с табличным значением F- критерия Фишера при уровне значимости α= 0,05
.
Если неравенство (2) выполняется, считается, что принятое уравнение линии регрессии статически значимо описывает результаты эксперимента.
Выборка:
| №№ п/п | x(f) | y(f) | yср |
| 9,666667 | |||
| 15,33333 | |||
| 18,33333 | |||
| 30,33333 | |||
| 36,66667 | |||
| 48,66667 | |||
Сравниваются два уравнения линии регрессии: прямая и квадратная парабола.
а)Прямая линия
Вычисление необходимых сумм производится с помощью табл.1 После решения системы нормальных уравнений имеем:
a=-10,6 b=1,9
Среднее значение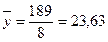 
Общая дисперсия:
Остаточная дисперсия:
| №№п/п | х | у | х² | х³ | х^4 | ху | х²у |
| 9,666667 | 96,66667 | 966,6667 | |||||
| 15,33333 | 199,3333 | 2591,333 | |||||
| 18,33333 | 293,3333 | 4693,333 | |||||
| 30,33333 | 667,3333 | 14681,33 | |||||
| 36,66667 | 916,6667 | 22916,67 | |||||
| 48,66667 | 1362,667 | 38154,67 | |||||
| Σ |
| № | х | у | (у-ˉу)² | ˉу=a+bx | ˉy=a+bx+cx² | ||
| ˉу | (y-ˉу)² | ˉу | (y-ˉу)² | ||||
| 19,14063 | 3,15 | 3,4225 | 9,419 | 19,52756 | |||
| 9,666667 | 71,5434 | 0,444444 | 12,623 | 8,739907 | |||
| 15,33333 | 180,0069 | 14,85 | 0,233611 | 16,709 | 1,892459 | ||
| 18,33333 | 257,3351 | 20,7 | 5,601111 | 21,677 | 11,18011 | ||
| 478,5156 | 26,55 | 2,4025 | 27,527 | 6,385729 | |||
| 30,33333 | 704,4601 | 32,4 | 4,271111 | 34,259 | 15,41086 | ||
| 36,66667 | 1029,34 | 38,25 | 2,506944 | 41,873 | 27,10591 | ||
| 48,66667 | 1813,34 | 44,1 | 20,85444 | 50,369 | 2,897939 | ||
| Σ | 4553,682 | 39,73667 | 93,14047 |
Отношение дисперсий:
Принятое уравнение линии регрессии статически значимо описывает результаты эксперимента.
б) Квадратная парабола
Порядок решения аналогичный.
a=5,373 b=0,235 c=0,049
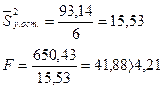
Вывод: По результатам расчетов можно заключить, что оба уравнения удовлетворительно описывают эмпирическую зависимость. За линию регрессии принимается квадратная парабола
, поскольку она дает большее значение F.
