Местная устойчивость стенок подкрановых балок проверяется также, как и у обычных балок. Условная гибкость стенки: 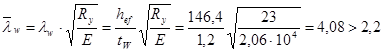 . Необходимо установить поперечные ребра жесткости с шагом не более 2hw = 2
. Необходимо установить поперечные ребра жесткости с шагом не более 2hw = 2 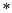 1,464 = 2,928 (м) при
1,464 = 2,928 (м) при 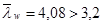 . Принимаем шаг 2 м.
. Принимаем шаг 2 м.
Ширина ребра bh 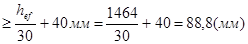 , принимаем bh = 90 мм.
, принимаем bh = 90 мм.
Толщина ребра: tS 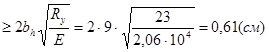 , принимаем tS = 8 мм.
, принимаем tS = 8 мм.
Размеры ребер жесткости приняты согласно п.7.10 [1]. Необходима проверка устойчивости, т.к. 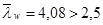 (наличие местных напряжений (sloc
(наличие местных напряжений (sloc 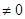 ) в балках с двусторонними поясными швами).
) в балках с двусторонними поясными швами).
Согласно п.7.6 [1] расчет на устойчивость стенок балок симметричного сечения, укрепленных только поперечными ребрами жесткости при наличии местн. напряж-я следует выполнять по ф-ле:
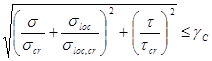 ,
,
где 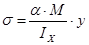 ,
, 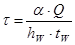 - действующие нормальные и касательные напряжения;
- действующие нормальные и касательные напряжения;
М и Q – средние значения соответственно момента и поперечной силы в пределах отсека;
a = 1,05 – для балок пролетом 12м;
scr и tcr – критические нормальные и касательные напряжения;
у = h0 / 2 = 1482 / 2 = 741(мм) = 74,1(см); h0=1500-18=1482 (мм).
Необходима проверка крайнего и среднего отсеков.
Крайний отсек.
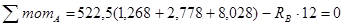 è
è 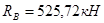 ;
;
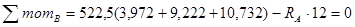 è
è 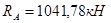 .
.
I – участок:
Q = RA = 1041,78 кН;
M = RA*x; М(0)=0; М1(0,536)=558,39 кН; М2(1,268)=1320,98 кН.
II – участок:
Q = RA – 522,5 = 519,28 (кН);
М = RA(1,268 + x) –522,5*х = 0; М(0)=1320,98 кН; М3(0,732)=1701,09 кН;М(1,51)=2105,09 кН.
III – участок:
Q = RA – 522,5*2 = -3,22 (кН);
М = RA(2,778 + х) –522,5(1,51 + х) –522,5*х = 0; М(0)=2105,09 кН; М(5,25)=2088,16 кН.
IV – участок:
Q = -RВ = -525,72 кН;
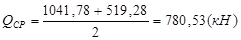 ,
, 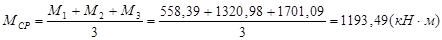
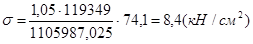 ,
, 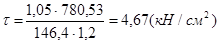 .
.
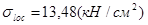 - см. "проверка прочности сечений";
- см. "проверка прочности сечений";
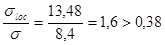 - табл.24, [1];
- табл.24, [1];
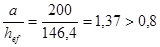 ;
; 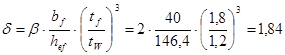 ;
;
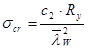 , где с2 = 51,66 (табл.25, [1]);
, где с2 = 51,66 (табл.25, [1]);
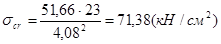 ,
,
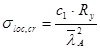 , где с1 = 30,374 (табл.23, [1]),
, где с1 = 30,374 (табл.23, [1]), 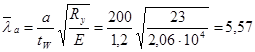 ;
;
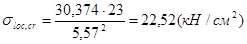 ;
;
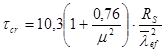 , где m - отношение большей стороны пластинки к меньшей;
, где m - отношение большей стороны пластинки к меньшей;
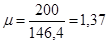 ; RS = 0,58*23 = 13,34 (кН/см2) – расчетное сопротивление сдвигу.
; RS = 0,58*23 = 13,34 (кН/см2) – расчетное сопротивление сдвигу.
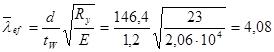 ,
,
где d = 146,4 см – меньшая из сторон пластинки (hef или а);
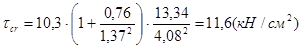 .
.
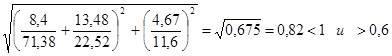 .
.
Средний отсек.
Построим эпюры М и Q.
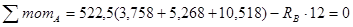 è
è 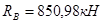 ;
;
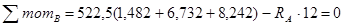 è
è 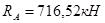 .
.
I – участок:
Q = RA = 716,52 кН;
M = RA*x; М(0)=0;М(3,758)=2692,68 кН.
II – участок:
Q = RA – 522,5 = 194,02 (кН);
М = RA(3,758 + x) –522,5*х = 0; М(0)=2692,68 кН; М(1,51)=2985,65 кН.
III – участок:
Q = RA – 522,5*2 = -328,48 (кН);
М = RA(5,268 + х) –522,5(1,51 + х) –522,5*х = 0; М(0)=2985,65 кН; М(5,25)=1261,13 кН.
IV – участок:
Q = -RВ = -850,98 кН;
Q = 194,02 кН; МСР = 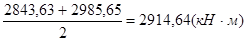 ;
;
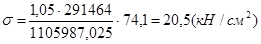 ,
, 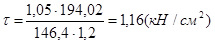 .
.
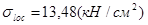 ;
; 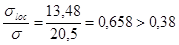 ;
;
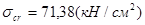 ,
, 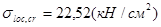 ;
; 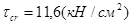 .
.
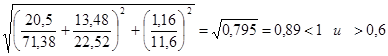 .
.
Q = 328,48 кН; МСР = 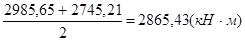 ;
;
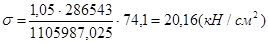 ,
, 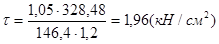 .
.
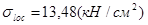 ;
; 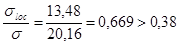 ;
;
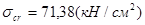 ,
, 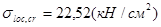 ;
; 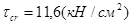 .
.
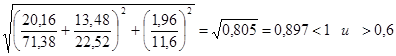 .
.
Расчет соединения поясов подкрановой балки со стенкой.
Соединение поясов подкрановой балки со стенкой осуществляется поясными швами. Швы делают сплошными, одинаковой наименьшей допустимой толщины по всей длине балки. Швы выполняем двусторонние, автоматической сваркой в лодочку сварочной проволокой СВ-0,8А.
Определим толщину шва (соединение стенки с верхним поясом):
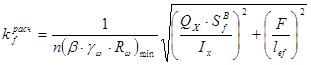
Rwf = 18 (кН/см2) – расчетное сопротивление угловых швов срезу по металлу шва (табл.56,[1]).
Rwz = 0,45Run = 0,45*36=16,2 (кН/см2) – то же, по металлу границы сплавления.
kfmin = 7 (мм) – (табл.38, [1]).
bf = 1,1, bz = 1,15 – кэффициенты проплавления шва (табл.34,[1]).
bf*gwf*Rwf = 1,1*1*18=19,8 (кН/см2).
bz*gwz*Rwz = 1,15*1*16,2=18,63 (кН/см2) – min
где gwf, gwz = 1 – коэффициенты условий работы шва.
QX = 1163,4 кН – по линии влияния Qmax.
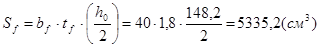 - статический момент пояса балки;
- статический момент пояса балки;
IX = 1105987,025см4 – момент инерции сечения балки;
lef = 35,52 см – длина распределения нагрузки от пояса на стенку;
F = 522,5 кН – расчетное значение вертикальной силы;
n = 2 – при двусторонних швах;
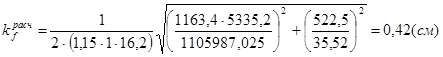 ,
,
kf 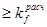 , kf
, kf 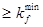 , принимаем kf = 7 мм.
, принимаем kf = 7 мм.
Соединение стенки с нижним поясом:
Вертикальные силы не действуют на нижний пояс, поэтому F = 0, следовательно:
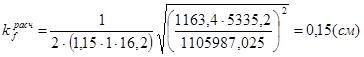 .
.
Принимаем: kf 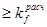 , kf
, kf 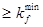 , è kf = 7 мм.
, è kf = 7 мм.
Расчет опорного ребра.
Балка опирается с помощью торцевых диафрагм. Торцы диафрагмы фрезеруются для непосредственной передачи опорного давления на оголовок колонны или опорный столик.
Размер опорных ребер торцевых диафрагм определяется из расчета на смятие:
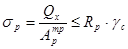 ;
;
где RP = Run/gm = Ru = 35 (кН/см2) – расчетное сопротивление стали смятию торцевой поверхности (табл.1, [1]).
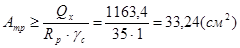 ,
,
принимаем Ah = bh*th = 22*1,6 =35,2 (см2) > АТР = 33,24 см2.
Проверка местной устойчивости ребра (п.п.7.24, табл.30, [1]):
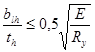 , где blh =
, где blh = 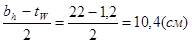 ;
;
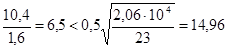 .
.
Проверка условной стойки:
А = Аh + tw*S = 35,2+1,2*23,34 = 63,21 (см2),
где 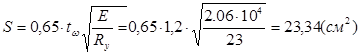 - часть стенки включающаяся в совместную работу с ребром;
- часть стенки включающаяся в совместную работу с ребром;
Момент инерции условной стенки относительно оси стенки (из плоскости балки):
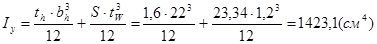 ,
,
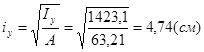 - радиус инерции.
- радиус инерции.
Проверим условную стойку на устойчивость из плоскости стенки:
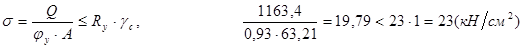
где jу = 0,930 – коэффициент продольного изгиба стойки (табл.72, [1]).
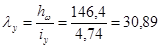 .
.




