Тема. Развитие представлений о природе света. Источники и приемники света. Распространение света в различных средах. Поглощение и рассеивание света

05.02.2015

Урок 39 (11 класс)

Тема. Развитие представлений о природе света. Источники и приемники света. Распространение света в различных средах. Поглощение и рассеивание света

1. Введение Оптика – раздел физики, который изучает световые явления и законы, установленные для них, а также взаимодействие света с веществом, природу света.

Информация о мире приходит к человеку посредством зрения. При помощи света мы получаем большую часть информации об окружающем мире. Первые сведения о свете появились 2,5 тысячи лет назад. Пифагор был одним из первых ученых, кто дал научную гипотезу относительно природы света (см. Рис. 1). Он первый не только догадался, но и доказал, что свет распространяется прямолинейно. Он, а затем и другие геометры, вплоть до Евклида, использовали световые явления отражения и преломления для построения основ геометрии. Недаром один из разделов оптики так и называется – геометрическая оптика.

Рис. 1. Пифагор

Пифагор: «Свет – поток частиц, которые излучают предметы, проникая в глаз человека, они приносят информацию о том, что же нас окружает».

В XVII веке сторонником этой теории стал Исаак Ньютон (см. Рис. 2). Он объяснял много световых явлений, основываясь на том, что свет – это поток специальных частиц. Ньютон не был столь категоричен в суждении о корпускулярной природе света и давал свои утверждения весьма обтекаемо, оставляя место сомнениям.

«Корпускула» происходит от лат. corpusculum – частица. Поэтому теория Ньютона стала называться корпускулярной теорией света.

Рис. 2. Исаак Ньютон

Факты: 1. Прямолинейное распространение света.

2. Закон отражения.

3. Закон образования тени от предмета.

В это же время появилась другая теория – волновая теория света. Сторонником этой теории был Христиан Гюйгенс (см. Рис. 3). Он пытался объяснить те же явления, что и Ньютон, только с той позиции, что свет – это волна.

Рис. 3. Христиан Гюйгенс

 

Гюйгенс построил волновую теорию света по аналогии с волновыми процессами на воде и в воздухе и потому считал, что световые волны также должны распространяться в какой-то упругой среде, которую назвал световым эфиром. Эта идея прослужила основой волновой оптики вплоть до начала XX века.

В те времена уже было замечено, что свет распространяется не только прямолинейно.

1. Свет может огибать препятствия – дифракция (см. Рис. 4).

Рис. 4. Дифракция

2. Волны могут складываться – интерференция (см. Рис. 5).

Рис. 5. Интерференция

Эти явления свойственны только волнам, поэтому Гюйгенс считал, что свет – это волна.

Корпускулярная теория не могла объяснить, как один луч проходит через другой. Если рассматривать свет как поток частиц, то должно наблюдаться взаимодействие, а его не наблюдалось, и это говорило в пользу того, что свет – волна.

В середине XIX века была создана теория Максвелла. Он доказал, что электромагнитное поле распространяется со скоростью 300 тысяч км в сек. Вследствие проведенных опытов было выяснено, что с такой скоростью распространяется и свет.

Свет – частный случай электромагнитной волны.

XVII в. – датский ученый Ремер провел эксперимент, в котором выяснилось, что скорость распространения света равна примерно 300 тысяч км в сек.

1848 г. – Ипполит Физо доказал, что скорость света составляет 300 тысяч км в сек.

Это все подтверждало тот факт, что свет является электромагнитной волной.

В XIX веке Генрих Герц (см. Рис. 6) изучал свойства электромагнитных волн и показал, что свет может быть частицей. Герц открыл явление фотоэффекта.

Рис. 6. Генрих Герц

Генрих Герц изучал электромагнитные волны, изначально считая, что их не существует, и проявил настоящее мужество, первым признав их реальность как природного объекта.

Фотоэффект: под действием света из металлической пластины, заряженной отрицательно, выбиваются электроны.

Это может выполняться только в том случае, если свет – поток частиц.

В XX веке пришли к окончательному решению, введя понятие корпускулярно-волнового дуализма света.

Свет ведет себя при распространении как волна (волновые свойства), а при излучении и поглощении – как частица (со всеми свойствами частиц). То есть свет имеет двойную природу.

Поэтому все явления рассматриваются с позиций этих двух теорий.

 

2.Скорость света
Когда мы поворачиваем выключатель, то вся комната сразу же озаряется светом. Кажется, что свету совсем не надо времени, чтобы достигнуть стен. Предпринимались многочисленные попытки определить скорость света. Для этого пытались измерить по точным часам время распространения светового сигнала на большие расстояния (несколько километров). Но эти попытки не дали результата. Начали думать, что распространение света совсем не требует времени, что свет любые расстояния преодолевает мгновенно. Однако оказалось, что скорость света не бесконечно велика, и эта скорость была в конце концов измерена.

 

Астрономический метод измерения скорости света, скорость света впервые удалось измерить датскому ученому О. Рёмеру в 1676 г. Рёмер был астрономом, и его успех объясняется именно тем, что он использовал для измерений очень большие, проходимые светом расстояния. Это расстояния между планетами Солнечной системы.

Рёмер наблюдал затмения спутников Юпитера — самой большой планеты Солнечной системы. Юпитер имеет четырнадцать спутников. Ближайший его спутник — Ио — стал предметом наблюдений Рёмера. Он видел, как спутник проходил перед планетой, погружался в ее тень и пропадал из поля зрения. Затем он опять появлялся, как мгновенно вспыхнувшая лампа. Промежуток времени между двумя вспышками оказался равным 42 ч 28 мин. Таким образом, эта «луна» представляла собой громадные небесные часы, через равные промежутки времени посылавшие свои сигналы на Землю.

Вначале измерения проводились в то время, когда Земля при своем движении вокруг Солнца ближе всего подошла к Юпитеру (рис. 8.2). Такие же измерения, проведенные несколько месяцев спустя, когда Земля удалилась от Юпитера, неожиданно показали, что спутник опоздал появиться из тени на целых 22 мин по сравнению с моментом времени, который можно было рассчитать, зная период обращения И_о.

Рёмер объяснял это так: «Если бы я мог остаться на другой стороне земной орбиты, то спутник всякий раз появлялся бы из тени в назначенное время; наблюдатель, находящийся там, увидел бы Ио на 22 мин раньше. Запаздывание в этом случае происходит оттого, что свет употребляет 22 мин на прохождение от места моего первого наблюдения до моего теперешнего положения». Зная время запаздывания появления Ио и расстояние, которым оно вызвано, можно определить скорость света, разделив это расстояние на время запаздывания. Скорость оказалась чрезвычайно большой, примерно 300 000 км/с. Потому-то крайне трудно определить время распространения света между двумя удаленными точками на Земле. Ведь за одну секунду свет проходит расстояние, большее длины земного экватора в 7,5 раза.

Лабораторные методы измерения скорости света. Впервые скорость света лабораторным методом удалось измерить французскому физику И. Физо в 1849 г.

В опыте Физо свет от источника, пройдя через линзу, падал на полупрозрачную пластинку 1 (рис. 8.3). После отражения от пластинки сфокусированный узкий пучок направлялся на периферию быстро вращающегося зубчатого колеса. Пройдя между зубцами, свет достигал зеркала 2, находящегося на расстоянии нескольких километров от колеса. Отразившись от зеркала, свет, прежде чем попасть в глаз наблюдателя, должен был пройти опять между зубцами. Когда колесо вращалось медленно, свет, отраженный отзеркала, был виден. При увеличении скорости вращения он постепенно исчезал. В чем же здесь дело? Пока свет, прошедший между двумя зубцами, шел до зеркала и обратно, колесо успевало повернуться так, что на место прорези вставал зубец, и свет переставал быть видимым.

При дальнейшем увеличении скорости вращения свет опять становился видимым. Очевидно, что за время распространения света до зеркала и обратно колесо успевало в этом случае повернуться настолько, что на место прежней прорези вставала уже новая прорезь.

Зная это время и расстояние между колесом и зеркалом, можно определить скорость света. В опыте Физо при расстоянии, равном 8,6 км, для скорости света было получено значение 313 000 км/с.

Было разработано еще много других, более точных лабораторных методов измерения скорости света. В частности, американский физик А. Майкельсон разработал весьма совершенный метод определения скорости света с применением вращающихся зеркал.

Была измерена скорость в различных прозрачных средах. Скорость света в воде была определена в 1856 г. Она оказалась в 4/3 раза меньше, чем в вакууме. Во всех других веществах она также меньше, чем в вакууме.

По современным данным, скорость света в вакууме равна 299 792 458 м/с (с точностью до ±1,2 м/с). Приближенно скорость света можно считать равной 3 • 10⁸ м/с. Это значение скорости света нужно обязательно запомнить.
Определение скорости света сыграло в науке очень важную роль. Была не только выяснена природа света, но и установлено, что никакое тело не может двигаться со скоростью, превышающей скорость света в вакууме. Это стало ясно после создания теории относительности, о которой пойдет речь в следующей главе.

3. Линза – прозрачное тело, ограниченное с двух сторон сферическими поверхностями.

Тонкая линза – линза, толщина которой много меньше радиусов сфер, ограничивающих ее поверхность. Обозначение линз на схемах (см. Рис. 1):

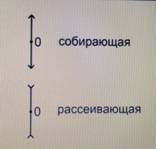Рис. 1. Обозначение линз на схемах

Типы линз (см. Рис. 2):

1. Двояковыпуклая

2. Двояковогнутая

3. Плосковыпуклая

4. Плосковогнутая

5. Выпукло-вогнутая

6. Вогнуто-выпуклая

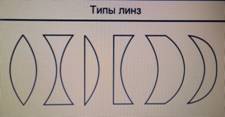Рис. 2. Типы линз

Свойство линз: преломление падающих на них лучей (Рис. 3).

Рис. 3. Свойства линз

Виды линз. Линза может быть ограничена двумя выпуклыми сферическими поверхностями (двояковыпуклая линза — рис. 8.24, а), выпуклой сферической поверхностью и плоскостью (плосковыпуклая линза — рис. 8.24, б), выпуклой и вогнутой сферическими поверхностями (вогнуто-выпуклая линза — рис. 8.24, в). Эти линзы посредине толпце, чем у краев, и все они называются выпуклыми.

Линзы, которые посредине тоньше, чем у краев, называются вогнутыми. Па рисунке 8.25 изображены три вида вогнутых линз: двояковогнутая — а, плосковогнутая — б и выпукло-вогнутая — в.

Главная оптическая ось – это линия, которая проходит через линзу перпендикулярно ее плоскости, она проходит через центры сфер, которые ограничивают поверхность линзы (О₁ и О₂).

Оптический центр – точка пересечения главной оптической оси с линзой.

Оптические оси линзы (см. Рис. 4):

Главный фокус линзы (F) – точка, расположенная на главной оптической оси, в которой пересекаются либо лучи, либо их продолжения.

Рис. 4. Оптические оси линзы

Если на собирающую линзу падают лучи, то они пересекаются в действительном фокусе F (см. Рис. 5).

Рис. 5. Собирающие линзы

Если на рассеивающую линзу падают лучи, то их продолжения пересекаются в мнимом фокусе F (см. Рис. 6).

Рис. 6. Рассеивающие линзы

Если лучи посылают на линзу из точки фокуса, то они, преломившись, должны пойти параллельно главной оптической оси (см. Рис. 7).

Рис. 7. Собирающая линза

Фокальная плоскость – плоскость, которая проходит через точку главного фокуса параллельно линзе.

Точка побочного фокуса (F^’) – точка пересечения фокальной плоскости и побочной оптической оси (см. Рис. 8).

Рис. 8. Точка побочного фокуса

Если послать луч параллельно побочной оптической оси, то он преломится таким образом, что обязательно пройдет через точку побочного фокуса линзы.

Фокусное расстояние (F, OF) – расстояние от оптического центра линзы до фокуса.

Оптическая сила (см. Рис. 9):

Рис. 9. Оптическая сила

Формула тонкой линзы (см. Рис. 10):

Рис. 10. Формула тонкой линзы

d – [м]; f – [м]

Правила расстановки знаков (см. Рис. 11):

Рис. 11. Правила расстановки знаков

Увеличение (Г) (см. Рис. 12):

Рис. 12. Увеличение

 

Построение изображения в линзах

Изображения:

1. Действительные – те изображения, которые мы получаем в результате пересечения лучей, прошедших через линзу. Они получаются в собирающей линзе;

2. Мнимые – изображения, образуемые расходящимися пучками, лучи которых на самом деле не пересекаются между собой, а пересекаются их продолжения, проведенные в обратном направлении.

Собирающая линза может создавать как действительное, так и мнимое изображение.

Рассеивающая линза создает только мнимое изображение.

Собирающая линза

1. Если предмет располагается за двойным фокусом.

Чтобы построить изображение предмета, нужно пустить два луча. Первый луч проходит из верхней точки предмета параллельно главной оптической оси. На линзе луч преломляется и проходит через точку фокуса. Второй луч необходимо направить из верхней точки предмета через оптический центр линзы, он пройдет, не преломившись. На пересечении двух лучей ставим точку А’. Это и будет изображение верхней точки предмета.

Точно так же строится изображение нижней точки предмета.

В результате построения получается уменьшенное, перевернутое, действительное изображение (см. Рис. 1).

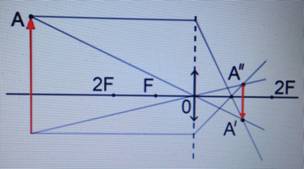Рис. 1. Если предмет располагается за двойным фокусом

2.Если предмет располагается в точке двойного фокуса.

Для построения необходимо использовать два луча. Первый луч проходит из верхней точки предмета параллельно главной оптической оси. На линзе луч преломляется и проходит через точку фокуса. Второй луч необходимо направить из верхней точки предмета через оптический центр линзы, он пройдет через линзу, не преломившись. На пересечении двух лучей ставим точку А’. Это и будет изображение верхней точки предмета.

Точно так же строится изображение нижней точки предмета.

В результате построения получается изображение, высота которого совпадает с высотой предмета. Изображение является перевернутым и действительным (Рис. 2).

Рис. 2. Если предмет располагается в точке двойного фокуса

3. Если предмет располагается в пространстве между фокусом и двойным фокусом

Для построения необходимо использовать два луча. Первый луч проходит из верхней точки предмета параллельно главной оптической оси. На линзе луч преломляется и проходит через точку фокуса. Второй луч необходимо направить из верхней точки предмета через оптический центр линзы. Через линзу он проходит, не преломившись. На пересечении двух лучей ставим точку А’. Это и будет изображение верхней точки предмета.

Точно так же строится изображение нижней точки предмета. В результате построения получается увеличенное, перевернутое, действительное изображение (см. Рис. 3).

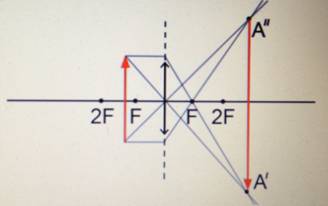
Рис. 3. Если предмет располагается в пространстве между фокусом и двойным фокусом

Так устроен проекционный аппарат. Кадр киноленты располагается вблизи фокуса, тем самым получается большое увеличение.

Вывод: по мере приближения предмета к линзе изменяется размер изображения.

Когда предмет располагается далеко от линзы – изображение уменьшенное. При приближении предмета изображение увеличивается. Максимальным изображение будет тогда, когда предмет находится вблизи фокуса линзы.

 

4. Если предмет находится в фокальной плоскости

Предмет не создаст никакого изображения (изображение на бесконечности). Так как лучи, попадая на линзу, преломляются и идут параллельно друг другу (см. Рис. 4).

Рис. 4. Если предмет находится в фокальной плоскости

 

5. Если предмет располагается между линзой и фокусом

Для построения необходимо использовать два луча. Первый луч проходит из верхней точки предмета параллельно главной оптической оси. На линзе луч преломится и пройдет через точку фокуса. Проходя через линзу, лучи расходятся. Поэтому изображение будет сформировано с той же стороны, что и сам предмет, на пересечении не самих линий, а их продолжений.

В результате построения получается увеличенное, прямое, мнимое изображение (см. Рис. 5).

Рис. 5. Если предмет располагается между линзой и фокусом

Таким образом устроен микроскоп.

Вывод(см. Рис. 6):

Рис. 6. Вывод

На основе таблицы можно построить графики зависимости изображения от расположения предмета (см. Рис. 7).

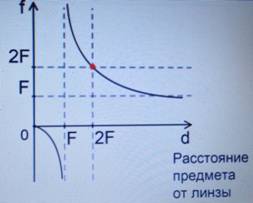
Рис. 7. График зависимости изображения от расположения предмета

 

График увеличения (см. Рис. 8).

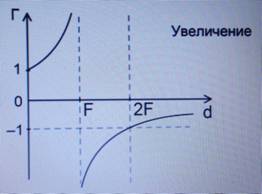Рис. 8. График увеличения

Построение изображения светящейся точки, которая располагается на главной оптической оси.

Чтобы построить изображение точки, нужно взять луч и направить его произвольно на линзу. Построить побочную оптическую ось параллельно лучу, проходящую через оптический центр. В том месте, где произойдет пересечение фокальной плоскости и побочной оптической оси, и будет второй фокус. В эту точку пойдет преломленный луч после линзы. На пересечении луча с главной оптической осью получается изображение светящейся точки (см. Рис. 9).

Рис. 9. График изображения светящейся точки

 

Рассеивающая линза

Предмет располагается перед рассеивающей линзой.

Для построения необходимо использовать два луча. Первый луч проходит из верхней точки предмета параллельно главной оптической оси. На линзе луч преломляется таким образом, что продолжение этого луча пойдет в фокус. А второй луч, который проходит через оптический центр, пересекает продолжение первого луча в точке А’, – это и будет изображение верхней точки предмета.

Таким же образом строится изображение нижней точки предмета.

В результате получается прямое, уменьшенное, мнимое изображение (см. Рис. 10).

Рис. 10. График рассеивающей линзы

При перемещении предмета относительно рассеивающей линзы всегда получается прямое, уменьшенное, мнимое изображение.

Формула тонкой линзы. Увеличение линзы

Выведем формулу, связывающую три величины: расстояние d от предмета до линзы, расстояние f от изображения до линзы и фокусное расстояние F.

1. Из подобия треугольников АОВ и A₁B₁O (см. рис. 8.37) следует равенство

Уравнение (8.10), как и (8.11), принято называть формулой тонкой линзы. Величины d, f и. F могут быть как поло-нсительными, так и отрицательными. Отметим (без доказательства), что, применяя формулу линзы, нуншо ставить знаки перед членами уравнения согласно следующему правилу. Если линза собирающая, то ее фокус действительный, и перед членом ставят знак «+». В случае рассеивающей линзы F < 0 и в правой части формулы (8.10) будет стоять отрицательная величина. Перед членом ставят знак «+», если изображение действительное, и знак «-» в случае мнимого изображения. Наконец, перед членом ставят знак «+» в случае действительной светящейся точки и знак «-», если она мнимая (т. е. на линзу падает сходящийся пучок лучей, продолжения которых пересекаются в одной точке).

 

В том случае, когда F, f или d неизвестны, перед соответствующими членами ставят знак «+». Но если в результате вычислений фокусного расстояния или расстояния от линзы до изображения либо до источника получается отрицательная величина, то это означает, что фокус, изображение или источник мнимые.

 

Увеличение линзы. Изображение, получаемое с помощью линзы, обычно отличается своими размерами от предмета. Различие размеров предмета и изображения характеризуют увеличением.

Линейным увеличением называют отноптение линейного размера изображения к линейному размеру предмета.

Для нахождения линейного увеличения обратимся снова к рисунку 8.37. Если высота предмета АВ равна h, а высота изображения А₁В₁ равна Н, то

есть линейное увеличение.

Из подобия треугольников АОВ и ОА₁В₁ следует, что

Следовательно, увеличение линзы равно отношению расстояния от изображения до линзы к расстоянию от линзы до предмета:

Линзы являются основной частью фотоаппарата, проекционного аппарата, микроскопа, телескопа. В глазу тоже есть линза — хрусталик.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

На рисунке 8.39 показано расположение главной оптической оси MN линзы, светящейся точки S и ее изображения S₁. Найдите построением оптический центр линзы и ее фокусы. Определите, собирающей или рассеивающей является эта линза, действительным или мнимым является изображение.
Решение. Луч, проходящий через оптический центр линзы, не отклоняется от своего направления. Поэтому оптический центр О совпадает с точкой пересечения прямых SS₁ и MN (рис. 8.40). Проведем луч SK, параллельный главной оптической оси. Преломленный луч KS₁ пройдет через фокус. Зная, что луч, падающий на линзу через фокус, после преломления идет параллельно главной оптической оси, находим другой фокус. Линза является собирающей, а изображение — действительным.

2. Изображение предмета имеет высоту Н = 2 см. Какое фокусное расстояние F должна иметь линза, расположенная на расстоянии f = 4 м от экрана, чтобы изображение данного предмета на экране имело высоту h = 1 м?

Решение. Из формулы линзы

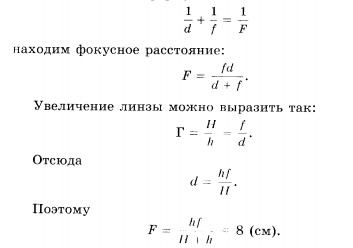
Домашнее задание

1. Т.Н.Засекина, Д.А.Засекин Е.В. Физика. 11класс, «Сиция», 2011.Читать §50 (с.195-197).

2. Ответить на вопросы (устно).
1. Постройте изображение предмета, помещенного перед собирающей линзой, в следующих случаях:

1) d > 2F; 2) d = 2F; 3) F < d < 2F; 4) d < F.

2. На рисунке 8.41 линия АВС изображает ход луча через тонкую рассеивающую линзу. Определите построением положения главных фокусов линзы.

3. Постройте изображение светящейся точки в рассеивающей линзе, используя три «удобных» луча.

4. Светящаяся точка находится в фокусе рассеивающей линзы. На каком расстоянии от линзы находится изображение? Постройте ход лучей.
5. Какие факты, связанные с распространением света, использовались сторонниками корпускулярной теории природы света?

6. Фотоэффект подтверждал волновую или корпускулярную концепцию о природе света?

7. Как называется концепция двойственной природы света?

8. В каких случаях свет нужно рассматривать как поток частиц?

9. Какую линзу называют тонкой?
10. Что называется главным фокусом линзы?
11. Какие лучи удобно использовать для построения изображения в линзе?
12. Что называется увеличением линзы?

13. Какой высоты должно быть плоское зеркало, висящее вертикально, чтобы человек, рост которого Н, видел себя в нем во весь рост?