Тема. Потенциальная энергия

25.12.2014

Урок 32 (10 класс)

Тема. Потенциальная энергия

1. Работа силы тяжести

Вычислим работу, используя в этот раз не второй закон Ньютона, а явное выражение для сил взаимодействия между телами в зависимости от расстояний между ними. Это позволит нам ввести понятие потенциальной энергии - энергии, зависящей не от скоростей тел, а от расстояний между телами (или от расстояний между частями одного и того же тела).
Вычислим сначала работу силы тяжести при падении тела (например, камня) вертикально вниз. В начальный момент времени тело находилось на высоте h₁ над поверхностью Земли, а в конечный момент времени - на высоте h₂ (рис.6.5). Модуль перемещения тела .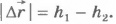

Направления векторов силы тяжести и перемещения совпадают. Согласно определению работы (см. формулу (6.2)) имеем

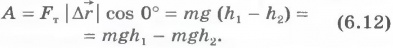
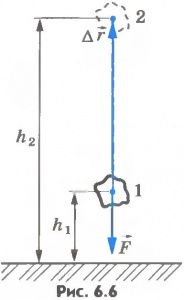
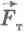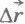Пусть теперь тело бросили вертикально вверх из точки, расположенной на высоте h₁, над поверхностью Земли, и оно достигло высоты h₂ (рис.6.6). Векторы и направлены в противоположные стороны, а модуль перемещения 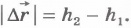. Работу силы тяжести запишем так:

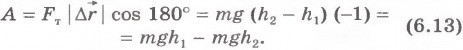
Если же тело перемещается по прямой так, что направление перемещения составляет угол с направлением силы тяжести (рис.6.7), то работа силы тяжести равна:

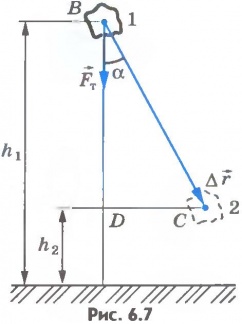Из прямоугольного треугольника BCD видно, что . Следовательно,

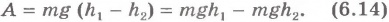
Формулы (6.12), (6.13), (6.14) дают возможность подметить важную закономерность. При прямолинейном движении тела работа силы тяжести в каждом случае равна разности двух значений величины, зависящей от положений тела в начальный и конечный моменты времени. Эти положения определяются высотами h₁ и h₂ тела над поверхностью Земли.
Более того, работа силы тяжести при перемещении тела массой m из одного положения в другое не зависит от формы траектории, по которой движется тело. Действительно, если тело перемещается вдоль кривой ВС (рис.6.8), то, представив эту кривую в виде ступенчатой линии, состоящей из вертикальных и горизонтальных участков малой длины, увидим, что на горизонтальных участках работа силы тяжести равна нулю, так как сила перпендикулярна перемещению, а сумма работ на вертикальных участках равна работе, которую совершила бы сила тяжести при перемещении тела по вертикальному отрезку длиной h₁-h₂.

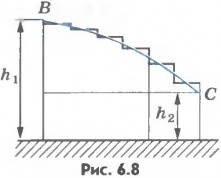
Таким образом, работа при перемещении вдоль кривой ВС равна:

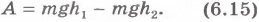
При движении тела по замкнутой траектории работа силы тяжести равна нулю. В самом деле, пусть тело движется по замкнутому контуру ВСDМВ (рис.6.9). На участках ВС и DМ сила тяжести 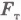совершает работы, равные по абсолютной величине, но противоположные по знаку. Сумма этих работ равна нулю. Следовательно, равна нулю и работа силы тяжести на всем замкнутом контуре.

Силы, обладающие такими свойствами, называют консервативными.
Итак, работа силы тяжести не зависит от формы траектории тела; она определяется лишь начальным и конечным положениями тела. При перемещении тела по замкнутой траектории работа силы тяжести равна нулю.

2. Работа силы упругости

Подобно силе тяжести, сила упругости тоже является консервативной. Чтобы убедиться в этом, вычислим работу, которую совершает пружина при перемещении груза.
На рисунке 6.10, а показана пружина, у которой один конец закреплен неподвижно, а к другому концу прикреплен шар. Если пружина растянута, то она действует на шар с силой 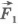(рис.6.10,б), направленной к положению равновесия шара, в котором пружина не деформирована. Начальное удлинение пружины равно 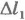. Вычислим работу силы упругости при перемещении шара из точки с координатой x₁ в точку с координатой x₂. Из рисунка 6.10, в видно, что модуль перемещения равен:

где 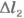- конечное удлинение пружины.

Вычислить работу силы упругости по формуле (6.2) нельзя, так как эта формула справедлива лишь для постоянной силы, а сила упругости при изменении деформации пружины не остается постоянной. Для вычисления работы силы упругости воспользуемся графиком зависимости модуля силы упругости от координаты шара (рис.6.11).

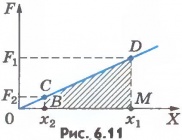
При постоянном значении проекции силы на перемещение точки приложения силы ее работа может быть определена по графику зависимости F_x от x и что эта работа численно равна площади прямоугольника. При произвольной зависимости F_x от x, разбивая перемещение на малые отрезки, в пределах каждого из которых силу можно считать постоянной, увидим, что работа будет численно равна площади трапеции.
В нашем примере работа силы упругости на перемещении точки ее приложения 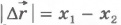численно равна площади трапеции ВCDM. Следовательно,

Согласно закону Гука и . Подставляя эти выражения для сил в уравнение (6.17) и учитывая, что 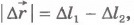, получим

Или окончательно

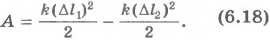
Мы рассмотрели случай, когда направления силы упругости и перемещения тела совпадали: 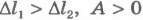. Но можно было бы найти работу силы упругости, когда ее направление противоположно перемещению тела или составляет с ним произвольный угол, а также при перемещении тела вдоль кривой произвольной формы.
Во всех этих случаях движения тела под действием силы упругости мы пришли бы к той же формуле для работы (6.18). Работа сил упругости зависит лишь от деформаций пружины и в начальном и конечном состояниях.
Таким образом, работа силы упругости не зависит от формы траектории и, так же как и сила тяжести, сила упругости является консервативной.

 

3. Потенциальная энергия

Используя второй закон Ньютона, что в случае движущегося тела работа сил любой природы может быть представлена в виде разности двух значений некоторой величины, зависящей от скорости тела, - разности между значениями кинетической энергии тела в конечный и начальный моменты времени:

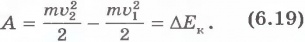
Если же силы взаимодействия между телами являются консервативными, то, используя явные выражения для сил, мы показали, что работу таких сил можно также представить в виде разности двух значений некоторой величины, зависящей от взаимного расположения тел (или частей одного тела):

Здесь высоты h₁ и h₂ определяют взаимное расположение тела и Земли, а удлинения и 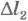- взаимное расположение витков деформированной пружины (или значения деформаций другого упругого тела).
Величину, равную произведению массы тела m на ускорение свободного падения g и на высоту h тела над поверхностью Земли, называют потенциальной энергией взаимодействия тела и Земли (от латинского слова «потенция» - положение, возможность).
Условимся обозначать потенциальную энергию буквой Е_п:

Величину, равную половине произведения коэффициента упругости k тела на квадрат деформации , называют потенциальной энергией упруго деформированного тела:

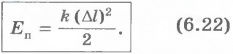
В обоих случаях потенциальная энергия определяется расположением тел системы или частей одного тела относительно друг друга.
Введя понятие потенциальной энергии, мы получаем возможность выразить работу любых консервативных сил через изменение потенциальной энергии. Под изменением величины понимают разность между ее конечным и начальным значениями, поэтому .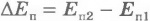
Следовательно, оба уравнения (6.20) можно записать так:

откуда .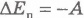
Изменение потенциальной энергии тела равно работе консервативной силы, взятой с обратным знаком.
Эта формула позволяет дать общее определение потенциальной энергии.
Потенциальной энергией системы называется зависящая от положения тел величина, изменение которой при переходе системы из начального состояния в конечное равно работе внутренних консервативных сил системы, взятой с противоположным знаком.
Знак «-» в формуле (6.23) не означает, что работа консервативных сил всегда отрицательна. Он означает лишь, что изменение потенциальной энергии и работа сил в системе всегда имеют противоположные знаки.
Например, при падении камня на Землю его потенциальная энергия убывает , но сила тяжести совершает положительную работу (A >0). Следовательно, A и 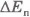имеют противоположные знаки в соответствии с формулой (6.23).
Нулевой уровень потенциальной энергии. Согласно уравнению (6.23) работа консервативных сил взаимодействия определяет не саму потенциальную энергию, а ее изменение.
Поскольку работа определяет лишь изменение потенциальной энергии, то только изменение энергии в механике имеет физический смысл. Поэтому можно произвольно выбрать состояние системы, в котором ее потенциальная энергия считается равной нулю. Этому состоянию соответствует нулевой уровень потенциальной энергии. Ни одно явление в природе или технике не определяется значением самой потенциальной энергии. Важна лишь разность значений потенциальной энергии в конечном и начальном состояниях системы тел.
Выбор нулевого уровня производится по-разному и диктуется исключительно соображениями удобства, т. е. простотой записи уравнения, выражающего закон сохранения энергии.
Обычно в качестве состояния с нулевой потенциальной энергией выбирают состояние системы с минимальной энергией. Тогда потенциальная энергия всегда положительна или равна нулю.
Итак, потенциальная энергия системы «тело - Земля» - величина, зависящая от положения тела относительно Земли, равная работе консервативной силы при перемещении тела из точки, где оно находится, в точку, соответствующую нулевому уровню потенциальной энергии системы.
У пружины потенциальная энергия минимальна в отсутствие деформации, а у системы «камень - Земля» - когда камень лежит на поверхности Земли. Поэтому в первом случае 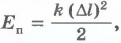, а во втором случае . Но к данным выражениям можно добавить любую постоянную величину C, и это ничего не изменит. Можно считать, что .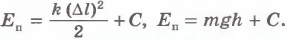
Если во втором случае положить 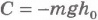, то это будет означать, что за нулевой уровень энергии системы «камень - Земля» принята энергия, соответствующая положению камня на высоте h₀ над поверхностью Земли.
Изолированная система тел стремится к состоянию, в котором ее потенциальная энергия минимальна.
Если не удерживать тело, то оно падает на землю (h =0); если отпустить растянутую или сжатую пружину, то она вернется в недеформированное состояние .
Если силы зависят только от расстояний между телами системы, то работа этих сил не зависит от формы траектории. Поэтому работу можно представить как разность значений некоторой функции, называемой потенциальной энергией, в конечном и начальном состояниях системы. Значение потенциальной энергии системы зависит от характера действующих сил, и для его определения необходимо указать нулевой уровень отсчета.

Домашнее задание:

1. Е.В. Коршак, А.И. Ляшенко, В.Ф. Савченко. Физика. 10 класс, «Генеза», 2010. Повторить §33 (с.115-116).

2. Решить задачи № 1-3 упражнения 22 (с. 117).

3. Учить лекционный материал.

Ответить на вопросы (устно):
1. Чему равна работа силы упругости при перемещении тела по замкнутой траектории?
2. Какие силы называют консервативными?

3. В чем состоит сходство кинетической энергии тела с потенциальной?

4. В чем состоит различие между кинетической энергией и потенциальной?