Екзаменаційні питання з дисципліни

«ЧИСЕЛЬНІ МЕТОДИ»

 

 

1. Предмет «Чисельні методи», його роль в сучасній науці.

2. Похибки та їх класифікація. Приклади. Основні причини виникнення похибок.

3. Основа методу та алгоритм знаходження числа .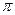

4. Основа методу та алгоритм знаходження числа .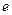

5. Ряд Тейлора для функції однієї змінної та його роль в чисельних методах. Приклад.

6. Похибка функції однієї змінної на основі її ряду Тейлора. Приклад.

7. Похибка площі кола при умові, що: а) похибка радіуса рівна 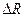; б) похибка числ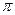а рівна .

8. Похибка об’єму кулі при умові, що: а) похибка радіуса рівна 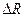; б) похибка числ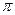а рівна .

9. Ряд Тейлора для функції двох змінних та його роль в чисельних методах. Приклад.

10. Похибки функції двох змінних на основі її ряду Тейлора. Приклад.

11. Похибка площі кола при умові, що похибка радіуса рівна 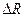, похибка числ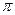а рівна .

12. Похибки функції багатьох змінних на основі її ряду Тейлора. Приклад.

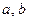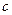13. Похибка об’єму прямокутного паралелепіпеда із ребрами і при умові, що похибки ребер відповідно рівн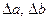і і .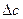

14. Ряд Маклорена для функції однієї змінної. Розклад в ряд функції .

15. Складання математичної таблиці для функції . Записати вираз для знаходження значення функції при 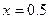(взяти перших сім членів ряду).

16. Формула Ейлера та її зв’язок з розкладами в ряди функцій 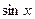та .

17. Ряд Маклорена для функції однієї змінної. Розклад в ряд функції 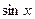. Записати вираз для знаходження значення функції 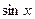при 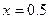(взяти перших сім членів ряду).

18. Складання математичної таблиці для функції .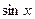

19. Ряд Маклорена для функції однієї змінної. Розклад в ряд функції . Записати вираз для знаходження значення функції при 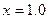(взяти перших сім членів ряду).

20. Складання математичної таблиці для функції .

21. Основні задачі числових методів алгебри.

22. Матриця. Основні види матриць. Транспонована матриця.

23. Основні дії над матрицями.

24. Обернена матриця. Приклади використання оберненої матриці.

25. Рівняння та їх класифікація. Приклади.

26. Числові методи розв’язку системи лінійних алгебраїчних рівнянь. Правило Крамера.

27. Метод Гауса розв’язку системи лінійних алгебраїчних рівнянь.

28. Постановка задачі та основні етапи розв’язку нелінійних рівнянь (знаходження коренів нелінійних рівнянь) числовими методами.

29. Способи відділення коренів нелінійних рівнянь.

 

1. Метод половинного ділення в задачі уточнення кореня нелінійного рівняння. Абсолютна похибка методу.

2. Метод Ньютона розв’язку (знаходження коренів) нелінійних рівнянь. Спрощений метод Ньютона.

3. Метод січних (хорд) розв’язку (знаходження коренів) нелінійних рівнянь.

4. Метод простих ітерацій розв’язку (знаходження коренів) нелінійних рівнянь. Приклад.

5. Постановка задачі чисельного диференціювання. Найпростіші формули числового диференціювання: різницева, центральна різницева та друга різницева похідні. Похибки різницевої, центральної різницевої та другої різницевої похідних.

6. Інтерполяційні многочлени та використання їх в задачах диференціювання.

7. Постановка задачі чисельного інтегрування функцій. Квадратурні формули прямокутників, трапецій, Симпсона (на прикладі одного елементарного відрізка). Похибки чисельного інтегрування.

8. Метод Монте-Карло обчислення інтегралів.

9. Задачі наближення функцій (експериментальних даних) та основні методи їх вирішення.

10. Сітка, рівномірна сітка, вузли інтерполяції. Приклад.

11. Постановка задачі інтерполяції. Приклад. Теорема про інтерполяційні поліноми (многочлени).

12. Інтерполяційний поліном. Визначення коефіцієнтів інтерполяційного полінома.

13. Інтерполяційний многочлен Лагранжа. Похибка інтерполяції.

14. Скінчені та розділені різниці. Інтерполяційний многочлен Ньютона. Похибка інтерполяції.

15. Сплайн-інтерполяція. Основні поняття сплайну. Поліноміальний сплайн.

16. Поліноміальний кубічний сплайн. Похибка наближення поліноміальними сплайнами.

17. Апроксимація функцій. Постановка задачі.

18. Основні етапи (пункти) апроксимації функції. Проблеми вибору апроксимуючої функції. Приклади.

19. Метод найменших квадратів і його використання в задачах апроксимації.

20. Міра (оцінка) відхилення функції апроксимації. Види оцінок.

21. Диференціальні рівняння як моделі реальних явищ, процесів. Класифікація диференціальних рівнянь.

22. Побудова диференціального рівняння радіоактивного розпаду.

23. Рівняння радіоактивного розпаду та основні задачі, які дозволяє розв’язувати це рівняння.

24. Побудова диференціального рівняння математичного маятника.

25. Записати умову задачі для виведення рівняння теплопровідності стержня та навести це рівняння.

26. Геометрична інтерпретація складових рівняння теплопровідності стержня та рівняння в цілому.

27. Різницевий аналог рівняння теплопровідності стержня.

28. Метод розв’язку рівняння теплопровідності стержня шляхом використання його різницевого рівняння.

29. Системи комп’ютерної математики Mathcad, Matlab, Maple, Excel. Їх достоїнства, недоліки.

 

Задачі для екзаменаційних білетів.

 

 

1. В обчисленнях для числа 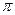використовується значення 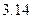. Записати його граничну абсолютну похибку.

2. Знайти граничну абсолютну похибку довжини кола, якщо його радіус 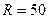, гранична абсолютна похибка 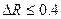, гранична абсолютна похибка .

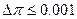3. Знайти граничну абсолютну похибку площі круга, якщо його радіус 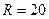, гранична абсолютна похибка 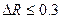, гранична абсолютна похибка .

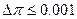4. Знайти граничну абсолютну похибку об’єму кулі, якщо її радіус 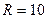, гранична абсолютна похибка 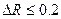, гранична абсолютна похибка .

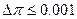5. Знайти абсолютну похибку об’єму прямокутного паралелепіпеда із ребрами 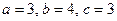, при умові, що похибки ребер відповідно рівні .

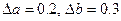6. Знайти абсолютну похибку об’єму прямокутного паралелепіпеда із ребрами 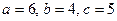при умові, що похибки ребер відповідно рівні .

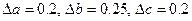7. Обчислення значення функції при 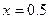(взяти перших п’ять членів ряду).

8. Обчислення значення функції 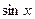при 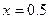(взяти перших п’ять членів ряду).

9. Обчислення значення функції при 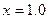(взяти перших п’ять членів ряду).

10. Знайти добуток двох матриць , .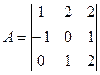

 

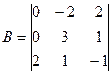11. До матриці 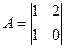знайти її обернену матрицю 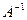. Результат перевірити.

 

12. Знайти розв’язок системи рівнянь за правилом Крамера:

 

 

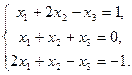
13. Обчислити наближене значення першої похідної у вузлах сітк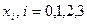и , при 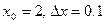. Значення функції у вузлах сітки задані в таблиці.

 

 

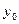
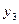
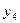
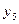
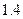
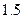
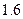
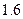
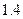
14. Обчислити наближене значення першої похідної у вузлах сітк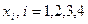и , при 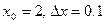. Значення функції у вузлах сітки задані в таблиці.

 

 

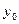
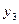
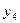
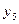
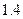
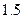
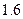
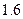
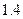
15. Обчислити наближене значення другої похідної у вузлах сітк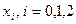и , при 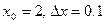. Значення функції у вузлах сітки задані в таблиці.

 

 

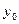
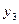
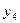
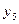
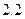
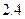
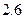
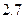
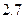
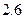
16. Обчислити наближене значення другої похідної у вузлах сітк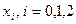и , при 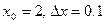. Значення функції у вузлах сітки задані в таблиці.

 

 

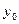
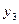
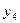
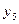
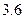
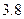
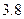
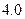
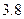
17. Побудувати інтерполяційний многочлен, використовуючи дані, наведені в таблиці.

 

 

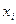
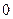
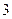
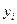
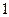
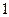
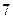
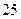
18. Побудувати інтерполяційний многочлен, використовуючи дані, наведені в таблиці.

 

 

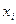
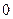
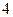
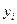
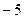
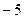
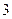
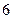
19. В таблиці наведені дані, отримані в результаті проведення експерименту:

 

 

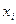
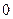
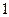
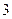
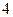
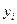
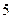
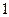
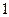
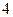
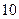
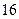
Проаналізувати ці дані і вказати клас функцій, представник якого може бути вибраний як функція апроксимації.

 

20. В таблиці наведені дані, отримані в результаті проведення експерименту:

 

 

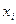
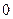
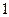
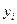
Побудувати функцію апроксимації, використовуючи при цьому МНК.

 

21. Функція апроксимації 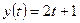. Використовуючи дані, наведені в таблиці, обчислити відхилення .

 

 

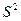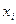
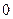
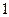
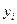
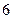
22. Функція апроксимації 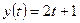. Використовуючи дані, наведені в таблиці, обчислити середньоквадратичне відхилення .

 

 

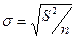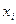
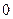
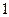
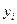
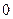
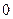
23. Навести основні класи диференціальних рівнянь та визначити тип диференціального рівняння .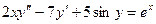

24. Вивести диференціальне рівняння радіоактивного розпаду. Записати розрахункову формулу визначення часу напіврозпаду та для визначити час напіврозпаду.

25. Вивести диференціальне рівняння коливання математичного маятника. Визначити довжину маятника, при якій період коливань 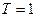сек.

26. Записати рівняння теплопровідності стержня. Дати геометричну інтерпретацію похідних 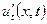та 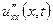, що входять в це рівняння.

27. Рівняння теплопровідності однорідного стержня має вигляд 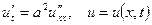, 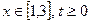. Обчислити значення температури стержня у вузлах сітки 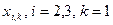, при умові, що 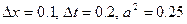. Початкова умова (температура стержня в початковий момент часу): .

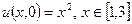28. Рівняння теплопровідності однорідного стержня має вигляд 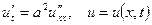, 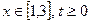. Обчислити значення температури стержня у вузлах сітки , при умові, що 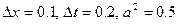. Початкова умова (температура стержня в початковий момент часу): .

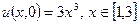29. Рівняння теплопровідності однорідного стержня має вигляд 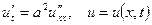, 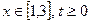. Обчислити значення температури стержня у вузлах сітки 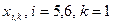, при умові, що 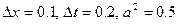. Початкова умова (температура стержня в початковий момент часу): .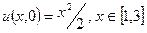