ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
САНКТ-ПЕТЕРБУРГСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ
ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА
КУРСОВАЯ РАБОТА ПО КУРСУ
ОСНОВЫ ТЕОРИИ ЦЕПЕЙ
РАСЧЕТ LC- И ARC-ФИЛЬТРОВ
ЗАДАНИЕ №12
Выполнил
Студент группы МТ-91
Любомирский Ю.А.
Проверил
__________________________
Санкт-Петербург
1. РАСЧЕТ LC-ФИЛЬТРА
1.1 СОДЕРЖАНИЕ ЗАДАНИЯ
Рассчитать LC-фильтр, полагая, что его элементы имеют пренебрежимо малые потери. Тип фильтра, вид аппроксимации, режим работы (вид нагрузки) и исходные требования к характеристике ослабления фильтра определяются вариантом курсовой работы.
Исходные данные для варианта 412-12:
· Тип фильтра: полосно-задерживающий фильтр (ПЗФ)
· Вид аппроксимации характеристики ослабления: по Баттерворту
· Режим работы фильтра: односторонняя нагрузка при заданном входном напряжении
Обозначения, используемые в работе:
· a0=30 дБ, гарантированное ослабление в полосах задерживания;
· 
, граничная частота полосы пропускания ФНЧ и ФВЧ;
= 17,826 кГц
· 
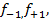граничные частоты полосы (полос) пропускания ППФ и ПЗФ;
· 
– граничная частота полосы задерживания ФНЧ и ФВЧ, а также одна из граничных частот полосы (полос) задерживания ППФ и ПЗФ
· 
– другая граничная частота полосы задерживания
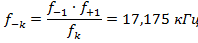
· Величина С задается преподавателем в пределах 
(C=0,5);
· Сопротивление нагрузки R=600 Ом;
· Допустимая неравномерность характеристики ослабления фильтра в полосе пропускания для фильтра с характеристикой Баттерворта составляет 
.
· Ослабление фильтра определяется выражением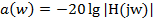 
.
1.2 Проектирование схемы фильтра
Для расчета фильтра используется методика, согласно которой схема, параметры элементов и характеристики проектируемого фильтра находятся с помощью частотного преобразования фильтра-прототипа нижних частот (ФПНЧ).
Порядок ФПНЧ рассчитывается по формуле (для фильтра с характеристикой Баттерворта):
Для ПЗФ: 
- нормированная граничная частота полосы задерживания ФПНЧ.
– нормирующий коэффициент
Округляем n до ближайшего большего целого числа, n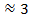 
.
Схема ФПНЧ для односторонней нагрузки при n=3:
Преобразование элементов ФПНЧ в элементы фильтров:
|
| L1= 751,3215 мГн, C1= 106,1033 нФ, L2= 14,3275 мГн, С2= 5,564 нФ, L3= 2,254 мГн, C3= 35,3678 нФ. |
1.3 Определение передаточной функции фильтра
Передаточная функция полиномиального ФПНЧ:
Где V(
) – полином Гурвица 3-ей степени, B = 
- коэффициент, определяющий величину ослабления фильтра на частоте 
V()= 
Передаточная функция проектируемого ПЗФ фильтра H(p) находится частотным преобразованием передаточной функции H() фильтра-прототипа нижних частот:
Передаточная функция ФПНЧ H():
Формула преобразования:
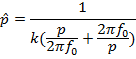
Передаточная функция фильтра H(p):
V(p)= 
Для вычисления коэффициентов квадратичных сомножителей полинома V(p) можно воспользоваться следующим алгоритмом:
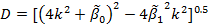
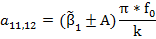
Результаты расчетов:
, 
, 
, 
, 
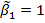
D=51,3473
A=0,1209
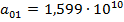
B=1
Итак:
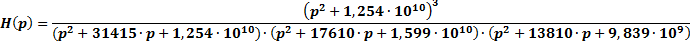
Сделаем проверку на маткаде:
|
|
|
|
|
|
|
|
|
|
|
|
Приведем ОПФ проектируемого ПЗФ к виду произведения из квадратичных сомножителей:
Итак окончательно получим ОПФ фильтра:
ОПФ, полученные аналитически и с помощью программы маткад, практически совпадают.
Частотная характеристика ослабления, построенная в программе маткад
Частотная характеристика ослабления фильтра a(w) с реальными параметрами, построенная в программе FASTMEAN
На граничной частоте 17,176 кГц ослабление составляет 34,67 дБ, на частоте 18,5 кГц ослабление составляет 34,61 дБ, что удовлетворяет условиям проектирования.
