Дати означення визначника ІІІ порядку.
Визначником третього порядку називається вираз:
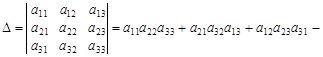
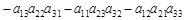 .
.
Визначник третього порядку можна обчислити за правилом трикутника. Перші три доданки, які беруть зі знаком плюс, є добутками елементів, що стоять на головній діагоналі і в вершинах двох трикутників, у яких одна сторона паралельна головній діагоналі.
Наступні три доданки, які беруть зі знаком мінус, є добутками елементів, що стоять на побічній діагоналі та у вершинах двох трикутників, у яких одна сторона паралельна побічній діагоналі.
Дати означення мінору довільного елемента визначника n-порядку.
Мінором Mij визначника n-порядку назв. визначник n-1 порядку, який отриманий з початкового шляхом ви креслення i-го рядка та j-го стовпчика.
Дослідження функції на монотонність.
Щоб дослідити функцію на монотонність, скористайтесь такою схемою:
- знайдіть область визначення функції;
- знайдіть похідну функції і область визначення похідної;
- знайдіть нулі похідної, тобто значення аргументу, при яких похідна дорівнює нулю;
- на числовому промені позначте спільну частину області визначення функції і області визначення її похідної, а на ній — нулі похідної;
- визначте знаки похідної на кожному з отриманих проміжків;
- за знаками похідної визначте, на яких проміжках функція зростає, а на яких спадає;
- запишіть відповідні проміжки через крапку з комою.
Еквівалентні нескінченно малі величини.
Еквівалентні нескінченно малі
Нескінченно малі α та β вважаються еквівалентними (в знаках α∼β), якщо їх різниця γ = β − α є величиною вищого порядку, ніж кожна з нескінченно малих α та β:
γ = o(α) та γ = o(β)
Загальна схема дослідження функції та побудова її графіку.
Нехай на відрізку [a;b] задана неперервна функція y=f(x), графіком якої є деяка лінія. Виникає запитання: як побудувати цей графік?
перш ніж будувати графік функції, її треба дослідити. Як правило, це слід робити за такою схемою.
1) Знайти область визначення функції.
2) Знайти точки перетину графіка з координатними осями.
Для цього треба розв'язати дві системи рівнянь:
y=f(x) і y=f(x)
y=0 x=0
3) Дослідити функцію на періодичність, парність і непарність.
4) Знайти значення функції на кінцях відрізків, де визначена функція. Якщо область визначення функції є інтервалом (пів інтервалом) або кількома інтервалами (пів інтервалами), то слід знайти граничне значення функції, коли х наближається до одного з кінців розглядуваних проміжків.
5) Знайти інтервали монотонності функції.
6) Знайти екстремальні точки функції і побудувати їх на площині.
7) На основі дослідження побудувати графік функції. Для зручності побудови графіка результати дослідження записують у таблицю.






