Московский государственный технический университет имени Н.Э.Баумана
Специализированный учебно-научный центр
ГОУ лицей №1580.
Вопросы к зачёту по математике.
й класс, 1-й семестр, 2014-2015 учебный год.
1) Множества. Способы задания множеств. Характеристическое свойство множеств. Равные множества, подмножества. Универсальное множество. Конечные и бесконечные множества. Пустое множество. Основные числовые и геометрические множества.
2) Операции пересечения и объединения множеств, их свойства. Диаграммы Эйлера-Венна.
3) Операции разности и дополнения множеств, их свойства. Диаграммы Эйлера-Венна.
4) Упорядоченные пары. Декартово произведение двух и более множеств, его свойства.
5) Соответствие между множествами. Область определения и множество значений соответствия. Способы задания соответствий. Граф и график соответствия.
6) Виды соответствий. Привести примеры.
7) Функциональное соответствие (функция), способы задания. Область определения и множество значений функции.
8) Обратная функция. Критерий обратимости функции. Сложная функция.
9) Числовые функции, их свойства (монотонность, ограниченность, чётность, периодичность).
10) Достаточное условие обратимости функций. Графики взаимно-обратных функций.
11) Свойства графиков чётных и нечётных функций. Арифметические теоремы о чётных и нечётных функциях.
12) Период, основной период функции. Теоремы о периодических функциях. Примеры.
13) Неопределяемые понятия и аксиомы стереометрии. Простейшие следствия из аксиом.
14) Взаимное расположение двух прямых в пространстве. Доказательство признака скрещивающихся прямых.
15) Взаимное расположение прямой и плоскости в пространстве. Доказательство признака параллельности прямой и плоскости.
16) Взаимное расположение плоскостей в пространстве. Доказательство теоремы о линии пересечения плоскостей, следствия. Теоремы о параллельных плоскостях.
17) Радианная и градусная меры углов. Тригонометрическая окружность. Соответствия между действительными числами и точками на тригонометрической окружности.
18) Определение синуса, косинуса, тангенса и котангенса действительного числа. Свойства и графики тригонометрических функций.
19) Основное тригонометрическое тождество. Формулы сложения. Формулы приведения. Тригонометрические формулы двойного угла, понижения степени и половинного аргумента. Универсальная тригонометрическая подстановка.
20) Формулы преобразования суммы (разности) тригонометрических функций в произведение и произведения тригонометрических функций в сумму (разность).
21) Формулы преобразования выражений вида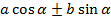 
с помощью дополнительного аргумента.
22) Линейная функция, её свойства и график. Общее уравнение прямой на плоскости. Признаки параллельности и перпендикулярности прямых на плоскости. Уравнение прямой, проходящей через две заданные точки. Угол между заданными прямыми. Пучок прямых.
23) Понятие модуля числа и модуля выражения. Уравнения и неравенства с модулем, основные равносильные переходы.
24) Квадратичная функция. Выделение полного квадрата. Вывод формулы корней квадратного уравнения, условия их существования и числа. Прямая и обратная теоремы Виета. Разложение квадратного трёхчлена на линейные множители.
25) Свойства и график квадратичной функции. Формулы координат вершины параболы. Исследование графика квадратного трёхчлена в зависимости от его коэффициентов.
26) Необходимые и достаточные условия расположения корней квадратного трёхчлена относительно заданного числа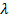 
.
27) Определение многочлена. Степень многочлена. Операции сложения и умножения многочленов. Корень многочлена. Деление многочлена на многочлен с остатком (столбиком и методом неопределённых коэффициентов).
28) Теорема Безу и её следствия. Схема Горнера. Понятие кратности корня многочлена.
29) Теоремы о целых и о рациональных корнях многочлена с целыми коэффициентами и их применение (примеры).
30) Обобщённая теорема Виета.
31) Дробно-рациональная функция. Правильная и простейшие рациональные дроби. Теорема о представлении рациональной дроби в сумму многочлена и правильной дроби.
32) Дробно-рациональная функция. Правильная и простейшие рациональные дроби. Разложение правильной рациональной дроби в сумму простейших дробей.
33) Степень с целым показателем. Степенная функция с натуральным и целым показателями, свойства и графики.
34) Корень n-й степени из числа. Алгебраический и арифметический корни. Функция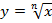 
.
35) Степень с рациональным показателем, её свойства. Степень с иррациональным показателем. Показательная функция.
36) Логарифм числа. Основное логарифмическое тождество. Свойство логарифмов. Формулы по логарифмам.
37) Логарифмическая функция, её свойства и график.
38) Понятие угла между параллельными, пересекающимися и скрещивающимися прямыми. Перпендикулярность прямой и плоскости. Признак перпендикулярности прямой и плоскости.
39) Теорема о трёх перпендикулярах.
40) Расстояние между фигурами. Доказательство существования и единственности общего перпендикуляра двух скрещивающихся прямых. Доказательство равенства расстояния между скрещивающимися прямыми длине их общего перпендикуляра.
УТВЕРЖДАЮ
Заведующий кафедры «Основы математики и информатики: С.С.Граськин
