Виды процессов переноса
Время релаксации – время в течение, которого система достигает равновесного значения.
Теплопроводность
Диффузия
Вязкость
Процессы переноса в газах
Общее уравнение переноса
Пусть 
- характеризует молекулярное свойство, отнесенное к одной молекуле (энергия, импульс, концентрация, эл. заряд и т.д.).
Пусть z направлено вдоль градиента G в направлении уменьшения.
Средняя длина свободного пробега молекул в данном направлении после последнего столкновения
– число частиц в dV.
- число частиц вылетает за dt из dV
учитывает убывания в результате столкновения
Поток числа молекул, пересекающих поверхность, равен
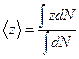- среднее расстояние вдоль z до ds
Средняя длина пробега от последнего столкновения и до пересечения площадки ds.
Энергия, импульс, эл. заряд, концентрация частиц …
Поток в направлении отрицательных значений оси x равен
,
.
Суммарный поток
Это уравнение переноса количества G.
Теплопроводность
G – средняя энергия теплового движения
Тогда уравнение переноса
Закон Фурье
Из-за 
легкие газы обладают большей теплопроводностью
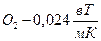
Т.к. 
и 
не зависят от 
теплопроводность не зависит от Р.
Вязкость
1860 Дж. Максвелл
- динамическая вязкость.
Т.к. 
и 
динамическая вязкость не зависит от давления и
зависит от 
Кинетическая вязкость 
Самодиффузи я
переносимая характеристика – концентрация отнесенная на одну молекулу.
, где
Уравнение Фика 
- коэффициент диффузии
При 
, т.е. 
При 
Связь между коэффициентами,
Характеризующими процессы переноса
удеальная теплоемкость
Уравнение самодиффузии зависящeе от времени
Самодиффузия – время в течение, которого происходит выравнивание температур, концентраций т.д.
Рассмотрим самодиффузию
Поток (изменение числа частиц в 
за 
) равен:
.
Разложим в ряд Тейлора:
Таким образом,
.
Тогда
Т.к. D не зависит от координат, запишем
- уравнение самодиффузии зависящее от времени.
В общем случае запишем:
или
,
где 
- оператор Лапласа.
Уравнение теплопроводности зависящее от времени
Аналогично
, где 
- удельная теплопроводность.
Но известно, что
, где у нас 
.
Т.е.
.
Время релаксации
Скорость приближения величины к равновесному значению считается пропорциональной ее отклонению от равновесного значения. Пусть 
- рассматриваемая величина.
.
Обратная величина коэффициента пропорциональности – время релаксации.
и
Физические явления в разряженных газах
Вакуум – когда давление настолько низкое, что молекулы сталкиваются в основном со стенками сосуда.
При нормальных условиях 
, но 
и при 
длина свободного пробега равна: 
.
В условиях вакуума правильнее говорить не о теплопроводности газа, а о теплопередаче, т.к. ни какого градиента температур нет.
Пример: сосуд Дьюара.
