Для записи решений и ответов на задания С1 – С6 используйте бланк ответов №2. Запишите сначала номер выполняемого задания, а затем полное обоснованное решение и ответ

Инструкция по выполнению работы

На выполнение экзаменационной работы по математике даётся

3 часа 55 минут (235 минут). Работа состоит из двух частей, включающих в себя 21 задание.

Часть 1 содержит 10 заданий (задания В1–В10) базового уровня сложности, проверяющих наличие практических математических знаний и умений.

Часть 2 содержит 11 заданий (задания В11–В15 и С1–С6) базового, повышенного и высокого уровней по материалу курса математики средней школы, проверяющих уровень профильной математической подготовки.

Ответом к каждому из заданий В1–В15 является целое число или конечная десятичная дробь. При выполнении заданий С1–С6 требуется записать полное решение и ответ.

Все бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается использование гелевой, капиллярной или перьевой ручки.

При выполнении заданий Вы можете пользоваться черновиком.

Обращаем Ваше внимание, что записи в черновике не будут учитываться при оценивании работы.

Советуем выполнять задания в том порядке, в котором они даны.

Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если после выполнения

всей работы у Вас останется время, Вы сможете вернуться к пропущенным заданиям.

Баллы, полученные Вами за выполненные задания, суммируются.

Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.

Желаем успеха!

Вариант ПА - т

Ч а с т ь 1

Ответом на задания В1 – В10 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланк ответов №1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений писать не нужно.

 

B1 Поезд Новосибирск – Красноярск отправляется в 17:20, а прибывает в 6:20 на следующий день (время указано московское). Сколько часов поезд находится в пути?

 

B2 При оплате услуг через платёжный терминал взимается комиссия 5%. Терминал принимает суммы кратные 10 рублям. Аня хочет положить на счет своего мобильного телефона не меньше 500 рублей. Какую минимальную сумму она должна положить в приемное устройство данного терминала?

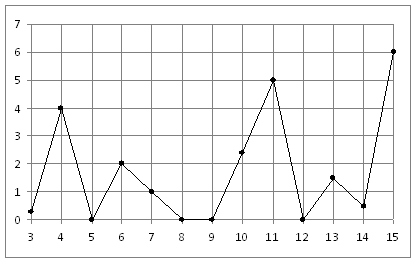
B3 На рисунке жирными точками показано суточное количество осадков, выпавших в Иркутске с 3 по 15 мая 2009 года. По горизонтали указываются числа месяца, по вертикали – количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода выпадало менее 2 миллиметров осадков.

B4 Клиент хочет арендовать автомобиль на двое суток для поездки протяженностью 1500 км. В таблице приведены характеристики трех автомобилей и стоимость их аренды. Помимо аренды клиент обязан оплатить топливо для автомобиля на всю поездку. Какую сумму в рублях заплатит клиент за аренду и топливо, если выберет самый дешевый вариант?

Автомобиль	Топливо	Расход топлива (л на 100 км)	Арендная плата (руб. за 1 сутки)
1.	Дизельное
2.	Бензин
3.	Газ

Цена дизельного топлива 30 руб. за литр, бензина 32 руб. за литр, газа 18 руб. за литр.

B5 Найдите площадь треугольника с координатами (1; 0), (3; 3) и (4; 2).

B6 В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 8 спортсменов из Дании, 7 спортсменов из Швеции и 5 – из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что последним выступит спортсмен из Норвегии. Результат округлите до сотых.

B7 Решите уравнение 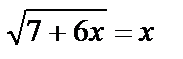. Если уравнение имеет более одного корня,

в ответе запишите сумму корней.

B8 В треугольнике ABC угол A равен 56⁰, угол B равен 72⁰, CH – высота. Найдите разность углов ACH и BCH. Ответ дайте в градусах.

B9 На рисунке изображён график функции 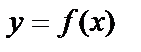и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке .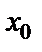

 

B10 Найдите угол ABD₁ прямоугольного параллелепипеда, для которого AB = 10, AD = 8, AA₁ = 6. Ответ дайте в градусах.

 

Не забудьте перенести все ответы в бланк ответов №1

 

Часть 2

Ответом на задания В11 – В15 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланк ответов №1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений писать не нужно.

 

B11 Найдите значение выражения .

B12 В боковой стенке цилиндрического бака вблизи дна закреплён кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нём меняется по закону , где t — время в минутах. Сколько секунд вода будет вытекать из бака?

B13 В правильной треугольной пирамиде SABC точка O – центр основания, S – вершина, SO = 12, AC = 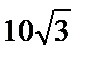. Найдите апофему боковой грани пирамиды.

B14 Из города А в город В выехал велосипедист. Через 1 ч 36 мин вслед за ним выехал мотоциклист и прибыл в город В одновременно с велосипедистом. Найдите скорость велосипедиста, если она меньше скорости мотоциклиста на 32 км/ч, а расстояние между городами А и В равно 45 км.

B15 Найдите на интервале точку минимума функции .

 

Не забудьте перенести все ответы в бланк ответов №1

 

Для записи решений и ответов на задания С1 – С6 используйте бланк ответов №2. Запишите сначала номер выполняемого задания, а затем полное обоснованное решение и ответ.

 

C1 а) Решите уравнение .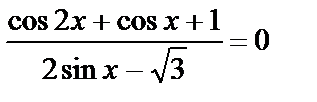

б) Найдите все корни этого уравнения, принадлежащие промежутку .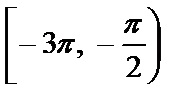

 

C2 Радиус основания конуса равен 8, а его высота равна 15. Плоскость сечения содержит вершину конуса и хорду основания, длина которой равна 14. Найдите расстояние от центра основания конуса до плоскости сечения.

C3 Решите систему неравенств

C4 Стороны АС, АВ, ВС треугольника АВС равны 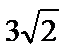, и 1 соответственно. Точка К расположена вне треугольника АВС, причём отрезок КС пересекает сторону АВ в точке, отличной от В. Известно, что треугольник с вершинами К, А и С подобен треугольнику АВС, а угол КАС – тупой.

а) Докажите, что угол АКС равен углу АСВ.

б) Найдите косинус угла АКС.

C5 Найдите все значения параметра а, при каждом из которых уравнение имеет нечётное число решений.

C6 Каждое из чисел n₁ , n₂ , …, n₃₅₀ равно 1, 2, 3 или 4. Обозначим , , , . Известно, что S₁ = 569.

а) Найдите S₄, если ещё известно, что S₂ = 1307, S₃ = 3953.

б) Может ли быть S₄ = 4857?

в) Пусть S₄ = 4785. Найдите все значения, которые может принимать S₂.