Покрытия здания
Рисунок 1.2.(а). Перекрытие здания.
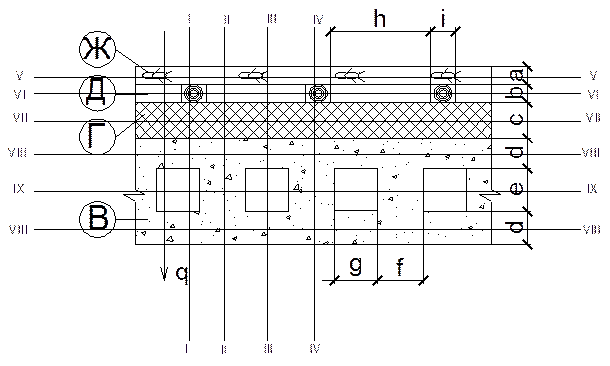
Рисонок 1.2.(б). Перекрытие здания с рассматриваемыми сечениями
- Битум нефтяной строительный (Ж), λ 1 =0,27;
- Сосна и ель поперек волокон (Д), λ 2 =0,18;
- Гравий керамзитовый (Г), λ 3 =0,23.
- Железобетон (В), λ 4 =2,04.
Конструктивное решение представлено на рисунке 1.2. Предварительно, для нахождения термического сопротивления перекрытия определили толщину искомого слоя Х. Для этого по таблице 5.1.[1] выбираем нормативное сопротивление теплопередаче Rнорм = 6,0(м2∙°С)/Вт.
Сопротивление искомого слоя находим по формуле:
Где,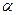 
в - коэффициент теплопередачи наружной поверхности ограждающей конструкции, [1, таблица5.4.];
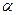н - коэффициент теплопередачи наружной поверхности ограждающей конструкции для зимних условий, применяемый по таблице 5.7 [1].
Определяем толщину искомого слоя:
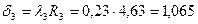м.
Разделим конструкцию на повторяющиеся элементы, приняв, что данные элементы имеют правильную геометрическую форму прямоугольника со сторонами 0,1х0,1.
Определим термическое сопротивление элементов при условии деления их плоскостями, параллельными тепловому потоку. Конструктивное решение представлено на рисунке 1.2.1.
Рисунок1.2.1(1) Элемент перекрытия
Рисунок1.2.1(2) Элемент перекрытия
Рисунок1.2.1(3) Элемент перекрытия
Рисунок1.2.1(4) Элемент перекрытия
Где Ri – термическое сопротивление каждого слоя конструкции, (м2∙°С)/Вт.
Железобетонную плиту разбиваем на три слоя: два слоя железобетона и слой воздушной прослойки.
(м2∙°С)/Вт.
(м2∙°С)/Вт.
(м2∙°С)/Вт.
(м2∙°С)/Вт.
Коэффициент теплопроводности замкнутой воздушной прослойки при толщине 0,089 (м), что примерно равно 0,1 (м) примем λ = 0,67(м2∙°С)/Вт.
Определяем площади элементов:
Термическое сопротивление элемента при условии деления его плоскостями параллельными тепловому потоку:
(м2∙°С)/Вт.
Находим термическое сопротивление элемента при условном делении его плоскостями, перпендикулярными тепловому потоку. Конструктивное решение представлено на рисунке 1.2.2.
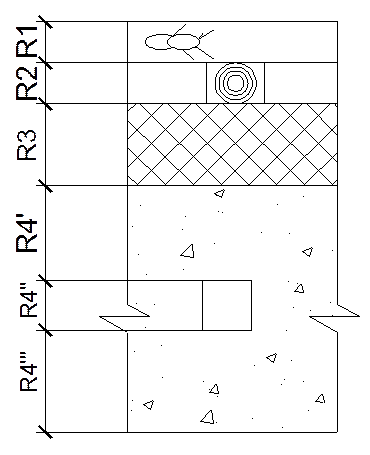
Рисунок 1.2.2 Конструкция перекрытия при условии деления его плоскостями, перпендикулярными тепловому потоку
(м2· 0С)/Вт;
(м2· 0С)/Вт;
(м2· 0С)/Вт;
(м2· 0С)/Вт;
(м2· 0С)/Вт;
Тогда,
Итак, получили: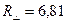 
(м2∙°С)/Вт. 
(м2∙°С)/Вт.
Так как термическое сопротивление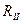 
не превышает величину 
более чем на 25%, то термический расчет конструкции выполняют согласно формуле:
(м2∙°С)/Вт.
Вывод: данная конструкция перекрытия удовлетворяет требованиям [1] по теплопроводности, так как нормативное сопротивление конструкции
Rнорм = 6,0(м2∙°С)/Вт., что меньше расчетного сопротивления R=6.41(м2∙°С)/Вт.
Расчет температурного поля в многослойной
Конструкции
Определим температуры на границах слоёв многослойной конструкции наружной стены, тепловой поток и глубина промерзания при следующих данных: 
Рисунок 2.1 – Наружная стена здания
- железобетон
λ 1 = 2,04 Вт/(м ∙°С); S1 = 19,70 Вт/(м2 ∙°С);
- плиты торфяные теплоизоляционные
λ 2 = 0,08 Вт/(м ∙°С); S2 = 2,34Вт/(м2 ∙°С);
- цементно-песчаный раствор
λ 3 = 0,93Вт/(м ∙°С); S3 = 11,09 Вт/(м2 ∙°С);
Рисунок 2.2 – Изменение температуры в наружной стене
Определяем термическое сопротивление каждого слоя материала:
Для определения тепловой инерции стены находим термическое сопротивление отдельных слоев конструкции по формуле:
,
где δ – толщина рассматриваемого слоя, м;
λ – коэффициент теплопроводности данного слоя, Вт/(м∙°С).
Вычислим термическое сопротивление отдельных слоев:
- железобетон
(м2 ∙ ºС)/Вт;
- плиты торфяные теплоизоляционные
(м2 ∙ ºС)/Вт;
- цементно-песчаный раствор
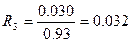(м2 ∙ ºС)/Вт;
=0,147+2,863+0,032=3,042 (м2 ∙ ºС)/Вт.
Определим тепловой поток через трехслойную конструкцию при разности температур двух сред:
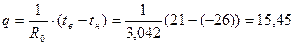Вт/м2,
где tв - температура внутреннего воздуха, °С;
tн - температура наружного воздуха, °С.
Определяем температуры на границах слоев конструкции по формуле:
,
где tx - температура в любой точке конструкции, °С;
Rx - часть термического сопротивления, находящегося между плоскостями c температурами t1 и tx, (м2 ∙ ºС)/Вт.
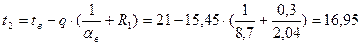ºС;
ºС;
ºС;
ºС;
Граница промерзания находится в слое торфяных плит.
Определяем глубину промерзания в теплоизоляционном слое и составляем пропорцию:
;
Отсюда х=0,09 м;
Общая глубина промерзания в этом случае составит:
δпр = х+0,03=0,12м.
Рисунок 2.3 – Глубина промерзания в теплоизоляционном слое
Рассмотрим данную задачу в случае, когда температура наружного и внутреннего воздуха поменяны друг с другом.
Рисунок 2.4 - Изменение температуры в наружной стене
Значение термического сопротивления всей конструкции и теплового потока в этом случае останется прежним:
0,147+2,863+0,032=3,042 (м2 ∙ ºС)/Вт.
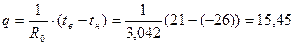Вт/м2.
Определяем температуры на границах слоев конструкции по формуле:
,
где tx - температура в любой точке конструкции, °С;
Rx - часть термического сопротивления, находящегося между плоскостями c температурами t1 и tx, (м2 ∙ ºС)/Вт.
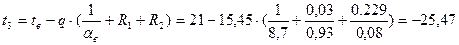ºС;
ºС;
ºС;
ºС;
Граница промерзания находится в слое торфяных плит.
Определяем глубину промерзания в теплоизоляционном слое и составляем пропорцию:
;
Отсюда х=0,1 м
Общая глубина промерзания в этом случае составит:
δпр =0,3+х =0,4м.
Рисунок 2.5 – Глубина промерзания в теплоизоляционном слое
Вывод: Глубина промерзания, в первом случае составляет 120 мм, во втором случае 400 мм. Экономически целесообразнее делать теплоизоляция как представлено в первом случае, при этом точка росы переносится в теплоизоляционный слой и стена незначительно промерзает в отличие от теплоизоляция, которая представлена во втором случае. При наружной теплоизоляции ограждающая конструкция аккумулирует тепло, потери тепла минимальны.
