СБОРНИК ЗАДАНИЙ
По
Сопротивлению материалов

ГОСУДАРСТВЕННЫЙ КОМИТЕТ РСФСР ПО ДЕЛАМ НАУКИ И ВЫСШЕЙ ШКОЛЫ
Казанский государственный архитектурно-строительный университет
Кафедра сопротивления материалов и основ теории упругости
СБОРНИК ЗАДАНИЙ
к расчетно-графическим работам по курсу «Сопротивление материалов с основами теории упругости и пластичности»
КАЗАНЬ–2009
Общая редакция Каюмова Р.А.,Страхова Д.Е.
УДК 539.3
Сборник заданий к расчетно-графическим работам по курсу «Сопротивление материалов с основами теории упругости и пластичности»/Каз. инж.-строит.ун-т; под общей редакцией Каюмова Р.А.,Страхова Д.Е. Казань, 2009. с.
Сборник заданий содержит исходные данные, расчетные схемы, постановку задач и перечень этапов работы при индивидуальном выполнении расчетно-графических работ студентами по курсу «Сопротивление материалов с основами теории упругости и пластичности»
Составители: сотрудники кафедры сопротивления материалов и основ теории упругости и пластичности.
Рецензенты: д.ф.-м.н. профессор Бутенко Ю.И.
(С) Казанский государственный архитектурно-строительный университет, 2009.
ОБЩИЕ УКАЗАНИЯ
К ВЫПОЛНЕНИЮ РАСЧЕТНО-ГРАФИЧЕСКИХ РАБОТ
Студент, в соответствии с составом каждого задания, выполняет свой вариант, который формируется по индивидуальному шифру. Шифр выдается студенту преподавателем – консультантом и представляет собой два числа, записанные в одну строку через черточку. Первое число шифра двухзначное, оно соответствует номеру фамилии студента в списке учебной группы. Этим числом определяется в задании номер расчетной схемы или тип сечений. В некоторых заданиях первая часть шифра не используется (например, в задании № 6). Вторая часть шифра – четырехзначное число служит основанием для форсирования оставшихся исходных данных индивидуального задания. Для этого под цифрами шифра надо писать первые четыре буквы русского алфавита, например:
шифр 07 – 4 8 0 9
А Б В Г
Буквы указывают столбцы, а цифры – строки таблиц, где следует брать исходные данные. По отмеченному здесь шифру для выполнения первого задания следует принимать 7-ой тип сечения, в котором в соответствии с таблицей 1 равнополочный уголок – 60x60x6, прямоугольник – 260x12, двутавр – № 24, угол поворота осей 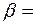 40°.
40°.
Студент обязан самостоятельно выполнять задания в полном объеме и сдавать их в установленные сроки, согласно графика учебного процесса. Задания принимаются последовательно, т.е. при условии сдачи предыдущих. Для получения дифференцированного зачета по расчетно-графической работе студент обязан предъявить преподавателю работу в оформленном виде, дать исчерпывающие ответы по основным вопросам теории, совпадающими с содержанием работы и показать умение решать задачи по данному разделу курса.
Выполненная расчетно-графическая работа оформляется в виде расчетно-пояснительной записки форматом 210x297 в соответствии с требованиями ЕСКД. В целях экономии бумаги разрешается опускать основные надписи на листах текстовой части и размещать текст записки на обоих сторонах листа.
Графическая часть расчета выполняется в виде чертежей формата А4 или производных форматов А4 х n, отвечающих требованиям ЕСКД и СПДС и брошюруется совместно с текстовой частью в определенной последовательности или в виде приложения в конце пояснительной записки.
ЗАДАНИЕ №1
ОПРЕДеление геометрических характеристик составного сечения
Для заданного составного сечения, состоящего из прямоугольного элемента, равнополочного уголка, швеллера или двутавра, требуется:
1. Найти общую площадь сечения.
2. Определить положение центра тяжести составного сечения относительно произвольно выбранных первоначальных осей.
3. Вычислить осевые и центробежный моменты инерции составного сечения относительно центральных осей, параллельных первоначально принятым.
4. Определить положение главных центральных осей инерции и вычислить главные моменты инерции составного сечения.
Типы сечений


таблица 1
| Г | В | Б | Г | |
| равнополочный уголок | прямоугольник | № двутавра или швеллера | о

| |
| 80х80х6 | 200х10 | |||
| 80х80х8 | 220х12 | |||
| 80х80х10 | 240х10 | |||
| 75х75х6 | 240х14 | |||
| 75х75х8 | 250х14 | |||
| 63х63х4 | 240х12 | |||
| 63х63х6 | 220х16 | |||
| 60х60х10 | 220х10 | |||
| 60х60х6 | 300х14 | |||
| 50х50х8 | 260х12 |
5. Вычислить осевые и центробежные моменты инерции относительно осей, повернутых на угол  относительно главных.
относительно главных.
6. По заданию преподавателя выполнить контроль результатов расчета с использованием персональных ЭВМ.
7. Определить положение главных центральных осей инерции, моменты инерции относительно этих осей, а также осевые и центробежные моменты инерции относительно осей, повернутых на угол  по отношению к главным, построением круга Мора.
по отношению к главным, построением круга Мора.
8. Вычертить составное сечение в приемлемом масштабе с указанием всех основных размеров и нанесением первоначальных, центральных и главных осей (формат А4).
9. Вычислить главные радиусы инерции, на втором чертеже (без нанесения размеров) построить эллипс инерции и определить осевые моменты инерции графическим способом относительно осей, повернутых на угол  по отношению к главным (формат А4).
по отношению к главным (формат А4).
10. Сопоставить результаты аналитического и графических способов решения.
11. При выполнении задания аналитические соотношения должны сопровождаться схематическими чертежами.
Задание в полном объеме выполняется студентами специальностей ПГС и АДА. Студенты других специальностей графические способы решения могут выполнять факультативно.
Литература
1. Терегулов И.Г. Сопротивление материалов и основы теории упругости и пластичности.- М.: Высшая школа, 1984, стр.207-227.
2. Смирнов А.Ф., Александров А.В. и др. Сопротивление
материалов.- М.: Высшая школа, 1975, стрЛ37-149.
3. Феодосьев В.И. Сопротивление материалов.- М.: Наука, 1986, стр.121-128.
ЗАДАНИЕ № 2
ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВ В ПОПЕРЕЧНЫХ СЕЧЕНИЯХ БРУСА И ПОСТРОЕНИЕ ЭПЮР
Для заданных расчетных схем требуется:
1. Определить опорные реакции.
2. Записать уравнения перерезывающих сил, изгибающих моментов и продольных (нормальных) сил для всех участков заданной схемы.
3. Вычислить значения перерезывающих сил, изгибающих моментов и нормальных сил в поперечных сечениях через один метр по длине участков. Для участков, где имеет место нелинейный закон изменения внутренних силовых факторов, ординаты эпюр вычислить не менее чем в четырех сечениях.
4. Произвести проверку эпюр на основе известных дифференциальных зависимостей, этот анализ кратко изложить в расчетно-пояснительной записке.
5. Для каждой схемы установить опасные сечения и расчетные значения внутренних силовых факторов.
6. По заданию преподавателя выполнить контроль построения эпюр внутренних силовых факторов  и
и  для схем А и Б с использованием персональных ЭВМ.
для схем А и Б с использованием персональных ЭВМ.
7. Вычертить расчетные схемы с эпюрами внутренних силовых факторов с указанием основных размеров и характерных ординат (формат А4 или А4 х n).
Исходные данные индивидуального задания выбираются из таблицы 2. Для схемы «Г» принять  0,8
0,8  и
и  .
.
Задание № 2 выполняются в полном объеме студентами специальностей 2903 и 2910. Студенты других специальностей выполняют это задание для схем "Б" и "В".
Литература
1. Терегулов И.Г. Сопротивление материалов и основы теории упругости и пластичности.- М.: Высшая школа. 1984 стр.25-51.
2. Смирнов А.Ф., Александров А.В. и др. Сопротивление материалов.- М.: Высшая школа, 1975, стр.13-16, 163-175.
3. Феодосьев В.И. Сопротивление материалов.- М.: Наука, 1986, стр.133-140.
Схема «А»


схема «Б»


|
СХЕМА «В»


таблица 2
| Г | А | Б | В | ||

|  (м) (м)
|  , кН/м , кН/м
|   , кН , кН
|   кНм кНм
| |
| 0.5 | 6.0 | ||||
| 0.4 | 3.0 | ||||
| 0.3 | 4.0 | ||||
| 0.25 | 4.5 | ||||
| 0.35 | 5.5 | ||||
| 0.6 | 6.5 | ||||
| 0.7 | 3.5 | ||||
| 0.45 | 6.0 | ||||
| 0.65 | 4.0 | ||||
| 0.55 | 4.5 |
схема «Г»



ЗАДАНИЕ № 3
РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ ШАРНИРНО-стержневой системы
Для заданной шарнирно-стержневой системы (см.схему), состоящей из абсолютно жесткого бруса и упругих стержней с заданными соотношениями площадей поперечных сечений, требуется:
1. Установить степень статической неопределимости.
2. Найти усилия в стержнях и опорные реакции от заданной внешней нагрузки.
3. Найти напряжения в стержнях от неточности изготовления  первого стержня. Знак плюс - стержень длиннее на величину
первого стержня. Знак плюс - стержень длиннее на величину  ; минус – короче.
; минус – короче.
4. Найти напряжения в стержнях от изменения температуры в первом и третьем стержнях. Коэффициент линейного расширения  [1/град].
[1/град].
5. Записать условия прочности для стержней от всех заданных воздействий. Выполнить их анализ и произвести подбор поперечных сечений стержней с учетом заданных соотношений площадей. Материал Ст-3,  160 МПа.
160 МПа.
6. Определить предельную грузоподъемность системы и допускаемую нагрузку, приняв постоянное соотношение между  и
и  . Коэффициент запаса прочности
. Коэффициент запаса прочности  1.5.
1.5.
7. По заданию преподавателя выполнить контроль результатов расчета с использованием персональных ЭВМ.
Расчетную схему системы принять согласно первой части шифра, а исходные данные из таблицы 3 – согласно второй части шифра.
Задание выполняется в полном объеме студентами специальностей ПГС и АДА. Студенты других специальностей выполняют расчет системы, исключив стержень 3, только на внешнее нагружение по допускаемым напряжениям и по допускаемой нагрузке.
Литература
1. Терегулов И.Г. Сопротивление материалов и основы теории упругости и пластичности.- М.: Высшая школа. 1984, стр.64-72.
2. Смирнов А.Ф., Александров А.В., и др. Сопротивление материалов.- М.: Высшая школа, 1975, стр.58-67.
3. Феодосьев В.И. Сопротивление материалов. М.: Наука, 1986, стр.33-44.
Схемы к заданию № 3



таблица 3
| А | Б | В | Г | Б | в | В | |||||
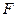 , кН , кН
|  , кН/м , кН/м
| 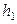 , м , м
|  , м , м
|  , м , м
|  , м , м
|  , м , м
| 
|  , мм , мм
| 
| 
| |
| 0.3 | 3/2 | ||||||||||
| -30 | -0.4 | 1/2 | |||||||||
| 0.5 | 3/2 | ||||||||||
| -25 | -0.6 | 3/4 | 3/2 | ||||||||
| 0.7 | 5/4 | 1/2 | |||||||||
| -35 | -0.4 | 1/2 | 4/5 | ||||||||
| 0.5 | 2/3 | 1/2 | |||||||||
| -0.7 | 1/2 | 4/5 | |||||||||
| -20 | -0.3 | 3/2 | 2/3 | ||||||||
| 0.6 | 2/3 | 5/4 |

ЗАДАНИЕ № 4
РАСЧЕТ БАЛКИ ПОСТОЯННОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ ПРИ ПЛОСКОМ ИЗГИБЕ
Для заданной расчетный схемы балки:
1. Определить опорные реакции.
2. Записать  перерезывающие силы и
перерезывающие силы и 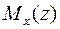 изгибающие моменты для произвольного сечения каждого из участков балки.
изгибающие моменты для произвольного сечения каждого из участков балки.
3. Вычислить перерезывающие силы и изгибающие моменты в характерных сечениях балки. На участках с криволинейным очертанием эпюр  подсчет ординат выполнить в сечениях через один метр, но не менее чем в четырех сечениях в пределах участка. Установить опасное сечение и расчетные значения внутренних силовых факторов.
подсчет ординат выполнить в сечениях через один метр, но не менее чем в четырех сечениях в пределах участка. Установить опасное сечение и расчетные значения внутренних силовых факторов.
4. Подобрать стальную балку стандартного двутаврого профиля и проверить прочность балки по теории прочности наибольших касательных напряжений, приняв  160МПа.
160МПа.
5. Вычислить нормальные и касательные напряжения в ряде точек произвольного поперечного сечения балки, в котором изгибающий момент и перерезывающая сила не равны нулю. По этим данным построить эпюры нормальных и касательных напряжений.
6. Записать дифференциальные уравнения изогнутой оси балки для всех ее участков.
7. Выполнить интегрирование дифференциальных уравнений и определить константы интегрирования.
8. Вычислить значения углов поворота сечений и прогибов балки не менее чем в четырех точках на каждом участке, включая их экстремальные значения. Рекомендуется вычислять углы поворота сечений и прогибы увеличенными в  раз. Результаты вычислений представить в табличной
раз. Результаты вычислений представить в табличной
Схемы к заданию №4


таблица 4
| А | Б | В | Г | |||
 (м) (м)
|  (м) (м)
| 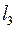 , (м) , (м)
|   , кН , кН
|  , кН/м , кН/м
|  кНм кНм
| |
| 4.5 | 4.0 | |||||
| 2.0 | 3.0 | 3.0 | ||||
| 3.0 | 4.0 | 2.5 | ||||
| 3.5 | 5.0 | 2.0 | ||||
| 6.0 | 1.5 | |||||
| 3.0 | 5.0 | 2.0 | ||||
| 2.0 | 5.0 | 4.0 | ||||
| 2.5 | Л.О | 3.0 | ||||
| 1.5 | 3.0 | 2.0 | ||||
| 3.0 | 2.0 | 1.5 |
форме.
9. По заданию преподавателя выполнить контроль результатов расчета с использованием персональных ЭВМ.
10. Проверить балку на жесткость по максимальным прогибам консоли и пролета. Допускаемый прогиб в пролете составляет
 , а на консоли
, а на консоли 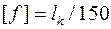
Здесь  длина пролета,
длина пролета,  длина консольной части балки. Если условия жесткости не удовлетворяются, то подобрать новое сечение балки
длина консольной части балки. Если условия жесткости не удовлетворяются, то подобрать новое сечение балки
11. В графической части расчетно-пояснительной записки должны быть представлены:
а) Расчетная схема балки с указанием размеров и нагрузок;
б) Эпюра перерезывающих сил;
в) Эпюра изгибающих моментов;
г) Эпюра углов поворота сечений 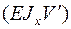 ;
;
д) Эпюра прогибов балки  ;
;
е) Эпюры нормальных и касательных напряжений в поперечном сечении балки.
Исходные данные принимаются по второй части шифра из таблицы 4.
Литература
1. Терегулов И.Г. Сопротивление материалов и основы теории упругости и пластичности.- М.: Высшая школа. 1984, стр. 227-238, 245-266.
2. Смирнов А.Ф., Александров А.В. и др. Сопротивление материалов,- М.: Высшая школа, 1975, стр.163-194, 212-230.
3. Феодосьев В.И. Сопротивление материалов. М.: Наука, 1986, стр.140-165.
ЗАДАНИЕ № 5
РАСЧЕТ БРУСА ПРИ СЛОЖНОМ СОПРОТИВЛЕНИИ
I. Для заданной расчетной схемы (1-28) системы рамного типа из прямых стержней с различными сечениями, жестко соединенных в узлах под прямым углом, необходимо:
а) Записать в принятой системе прямоугольных координат аналитические выражения внутренних силовых факторов по участкам, вычислить их значения в характерных точках, построить эпюры внутренних силовых факторов. Длины стержней и величину нагрузок принять в соответствии с шифром по таблице 5.
б) Установить, какую сложную деформацию испытывает каждый стержень системы. Задать форму сечения на каждом участке. На участке, испытывающем сложное сопротивление без кручения, принять форму сечения в виде стандартного двутавра. Для участка, испытывающего сложное сопротивление с кручением, принять круглое поперечное сечение. На оставшихся участках принять поперечное сечение в виде прямоугольника с заданным соотношением сторон  (таблица 5).
(таблица 5).
в) Установить местоположение расчетных (опасных) сечений на каждом участке системы.
г) По величинам внутренних силовых факторов, действующих в расчетных сечениях, из условий прочности подобрать размеры сечений стержней. Подбор размеров сечений должен сопровождаться анализом напряженного состояния, включающим в себя определение положений силовой и нулевой линий, построение эпюр нормальных и касательных напряжений и нахождение расчетных точек в сечении. В случае необходимости проверяется прочность в ряде предположительно расчетных точек опасного сечения по одной из теорий прочности (III-ей или IV-ой). Материал:
РАСЧЕТНЫЕ СХЕМЫ

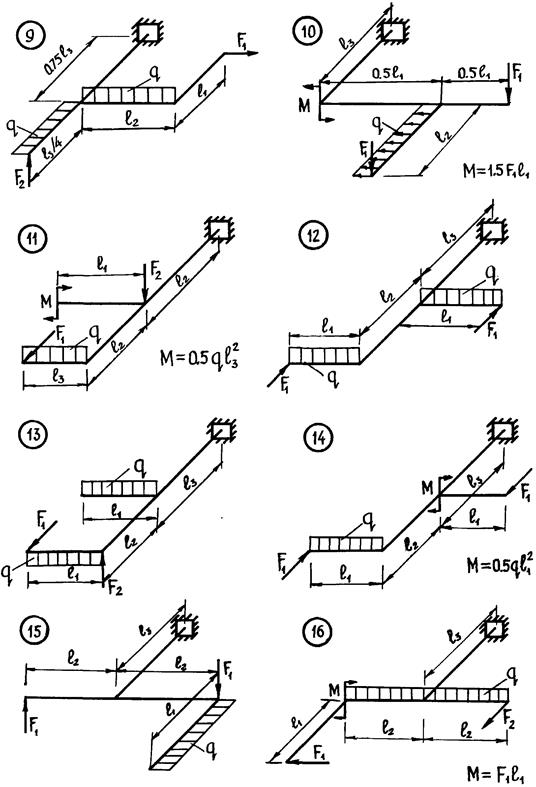


Таблица 5
| а | б | в | г | а | б | в | |
 (кН/м) (кН/м)
|  (кН) (кН)
|  (кН) (кН)
| 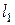 (м) (м)
|  (м) (м)
|  (м) (м)
| 
| |
| 1.0 | 1.9 | 1.2 | 1.2 | ||||
| 1.1 | 1.8 | 1.6 | 1.4 | ||||
| 1.2 | 1.7 | 1.4 | 1.6 | ||||
| 1.3 | 1.6 | 0.6 | 1.8 | ||||
| 1.4 | 1.5 | 0.8 | 2.0 | ||||
| 1.5 | 1.4 | 1.0 | 2.2 | ||||
| 1.6 | 1.3 | 1.5 | 2.4 | ||||
| 1.7 | 1.2 | 1.3 | 2.2 | ||||
| 1.8 | 1.1 | 1.7 | 2.0 | ||||
| 1.9 | 1.0 | 1.8 | 1.8 |
Расчетная схема стержня
(внецентренное сжатие)

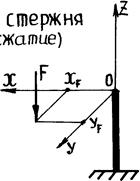

таблица 6
| А | Б | в | г | а | б | |
| сечение |  (м) (м)
|  (м) (м)
| 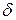 (м) (м)
| 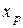 (м) (м)
|  (м) (м)
| |
| 0.16 | 0.32 | 0.030 | 0.015 | 0.020 | ||
| 0.18 | 0.30 | 0.020 | 0.017 | 0.018 | ||
| 0.20 | 0.28 | 0.015 | 0.020 | 0.016 | ||
| 0.22 | 0.26 | 0.020 | 0.023 | 0.014 | ||
| 0.24 | 0.24 | 0.030 | 0.025 | 0.012 | ||
| 0.26 | 0.22 | 0.015 | 0.030 | 0.010 | ||
| 0.28 | 0.20 | 0.032 | 0.012 | |||
| 0.30 | 0.18 | 0.030 | 0.035 | 0.014 | ||
| 0.32 | 0.16 | 0.015 | 0.030 | 0.016 | ||
| 0.16 | 0.32 | 0.020 | 0.020 | 0.018 |
двутавр – сталь 3, [  ] = 160МПа; – проверка по третьей теории прочности. Стержни круглого и прямоугольного сечений – легированная сталь [
] = 160МПа; – проверка по третьей теории прочности. Стержни круглого и прямоугольного сечений – легированная сталь [  ] = 250МПа; – проверка по четвертой теории прочности.
] = 250МПа; – проверка по четвертой теории прочности.
Плоскости наибольшей жесткости при изгибе двутаврового и прямоугольного сечений рекомендуется совместить с плоскостью действия наибольшей составляющей изгибающего момента  или
или  .
.
II. Для внецентренно сжатого стержня, изготовленного из материала разносопротивляющегося растяжению и сжатию [  ] = 30МПа, [
] = 30МПа, [  ] = 90 МПа;
] = 90 МПа;
а) Из условий прочности найти допустимое значение сжимающей силы [  ].
].
б) Построить эпюру нормальных напряжений в сечении при действии найденного значения допускаемой силы.
в) Построить ядро сечения.
Сечение стержня и координаты точек приложения силы в главных центральных осях заданы в таблице 6.
Литература
1. Терегулов И.Г. Сопротивление материалов и основы теории упругости и пластичности.- М.: Высшая школа, 1984, стр. 36-51, 316-324.
2. Смирнов А.Ф., Александров А.В. и др. Сопротивление материалов.- М.: Высшая школа, 1975, стр.273-292.
3. Феодосьев В.И. Сопротивление материалов.- И.: Наука,
1986, стр. 173-180.
ЗАДАНИЕ № 6






