Целью лабораторной работы является приобретение навыков по созданию генераторов псевдослучайных последовательностей и исследованию их свойств, а также по применю данных генераторов в реализации шифров гаммирования.
Требования к содержанию, оформлению и порядку выполнения
Отчет по выполнению лабораторной работы должен содержать: титульный лист, название работы, цель работы и содержательную часть.
В содержательной части отчета по выполнению лабораторной работы требуется привести:
· исходный текст и описание программной реализации генераторов псевдослучайных последовательностей на основе линейного конгруэнтного генератора или сдвигового регистра с линейной обратной связью, выбранных согласно своему варианту;
· результаты статистического анализа результатов их работы на основе критериев американского стандарта FIPS 140-1;
· описание шифра гаммирования, созданного на базе созданного генератора;
· результаты шифрования/расшифрования файла
· выводы по лабораторной работе.
Теоретическая часть
Описание принципов построения шифров гаммирования приведено в разделе 2.3.3. В этом же разделе рассматриваются и базовые примитивы, которые могут использоваться для этих целей. К ним относится линейные конгруэнтные генераторы (ЛКГ) и регистры сдвига с линейной обратной связью (РСЛОС). Строго говоря, эти генераторы не являются криптографическими, поскольку их выход предсказуем, но при соблюдении определенных условий случайная последовательность бит на их выходе выглядит случайно, т.е. удовлетворяет статистическим тестам на случайность.
Американский федеральный стандарт FIPS 140-1 определяет четыре статистических теста на случайность: монобитный тест, блочный тест (покер тест), тест серий, тест длин серий. Для этих тестов, задаются границы для удовлетворительных значений статистических параметров. Отдельная битовая последовательность длиной 20000 бит, получаемая из генератора, поддается каждому из четырех приведенных тестов. Если какой-нибудь тест не пройден, то считается, что генератор не прошел весь комплекс проверок.
Монобитный тест (частотный тест). Суть теста состоит в подсчете количества нулей и единиц на отрезке последовательности определенной длины. Пусть n 1 и n 2 обозначает число нулей и единиц в последовательности x, соответственно. Если последовательность случайная, то значения n 1 и n 2 должны удовлетворять условию 9654 < n 1 (n 2) < 10346.
Блочный тест (п окер – тест). Пусть m положительное целое число такое, что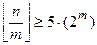 
и пусть 
. Последовательность последовательно разбивается на непересекающиеся подпоследовательности длиной m (m = 2,3,…). Пусть ni будет числом появлений i-го типа последовательности длиной m. Блочный тест определяет, действительно ли последовательности длиной m, появляются приблизительно столько же раз в последовательности x, сколько можно ожидать для случайной последовательности (каждая подпоследовательность – примерно равное число раз). Для применения критерия используется расчет параметра 
, где m – длина подсчитываемых неперекрывающихся подпоследовательностей (для данного стандарта принято m = 4), ni – количество появлений подпоследовательности i – того типа длины m (для m = 4 существует 2 m = 24 = 16 типов подпоследовательностей), k – общее количество неперекрывающихся подпоследовательностей длины m (для данного стандарта k = 20 000 / 4 = 5 000).
Этот параметр имеет распределение, близкое к распределению χ2 с
2 m – 1 степенями свободы. Статистика должна удовлетворять условию
1,03 < X 3< 57,4.
Тест серий. Под серией понимается последовательность одинаковых символов, то есть последовательно идущие единицы или нули. Суть теста состоит в том, что на заданной длине последовательности, которая тестируется, осуществляется подсчет серий длиной 1, 2, 3, 4, 5, 6 элементов (серии длиной более чем 6 элементов рассматриваются как серии длиной 6). Если последовательность случайная, то количество серий каждой длины должно находится в интервалах представленных в табл. Л2.1 (с увеличением длины серии на 1 – количество серий уменьшается примерно в 2 раза).
Таблица Л2.1
Интервалы для теста серий
| Длина серии | Необходимый интервал |
| 2267 – 2733 | |
| 1079 –1421 | |
| 502 – 748 | |
| 223 – 402 | |
| 90 – 223 | |
| 90 – 223 |
Тест длин серий. Суть теста состоит в проверке максимальной длины серии из одинаковых элементов. Если последовательность случайная, то максимальная длина серии не должна превышать значение 34.
Общая постановка задачи
В лабораторной работе требуется:
1. Изучить раздел 2.3.3 и теоретическую часть к данной лабораторной работе.
2. Разработать программу – генератор псевдослучайной последовательности бит для шифрования и расшифровывания текста при помощи шифра гаммирования. Программа должны обеспечивать:
· задание в командной строке режима работы (генерация гаммы с записью ее в файл/шифрование), имени входного файла, имени результирующего файла;
· ввод параметров генератора с клавиатуры;
· генерирование последовательности длиной 20000 бит с записью ее в файл для дальнейшего статистического анализа по критериям стандарта
FIPS 140-1;
· шифрование информации, находящейся в текстовом файле, с записью результата в другой файл.
3. Сформировать тестовую псевдослучайную последовательность и выполнить ее статистический анализ, на предмет удовлетворения требованиям стандарта FIPS 140–1.
4. Зашифровать и расшифровать файл, с использованием разработанной программы.
Для выполнения 2-го пункта задания можно воспользоваться программой TestFIPS1401.exe, любезно предоставленной кафедрой Безопасности информационных технологий Харьковского национального университета радиоэлектроники (см. Приложение №1).
Запустите приложение TestFIPS1401.exe. Для проведения статистического анализа необходимо:
· открыть файл, который содержит результаты работы генераторов, используя пункт меню "Файл", "Открыть файл" или кнопку "Файл" на панели управления;
· выбрать пункт меню "Файл", "Тестирование" или нажать кнопку "Тестирование" на панели управления.
Программа поддерживает возможность открытия нескольких файлов данных. Навигация по открытым файлам осуществляется с использованием кнопок "Назад" и "Вперед" на панели управления. После выполнения тестирования в поле окна выводятся результаты тестирования.
Основой для получения гаммы шифра должен выступать ЛКГ или РСЛОС. При выполнении лабораторной работы можно использовать параметры для ЛКГ представленные в таблице Л2.2, или самостоятельно сформировать необходимые параметры. Описание ЛГК в табл. Л2.2 дано в такой последовательности LCG(m, a, b, g 0).
Таблица Л2.2
Параметры линейных конгруэнтных генераторов
| № п/п | Имя | Описание |
| 1. | RANDU | LCG (231, 65539,0,1) |
| 2. | MINSTD | LCG(231-1, 16807,0,1) |
| 3. | MINSTD-25 | LCG(231-1, 1817129560,0,1) |
| 4. | ANSIC | LCG(231-1, 1103515245,12345,12345) |
| 5. | ANSIC-25 | LCG(231-1, 788950093,2103497953,12345) |
| 6. | ANSIC-203 | LCG(231-1, 1471780181,1584727831,12345) |
| 7. | Short SIM1 | LCG(230, 74125,227623267,1) |
| 8. | Short SIM2 | LCG(230, 982525,227623267,1) |
| 9. | Fisman LCG's | LCG(231-1, a, 0, 1) a = {599496926, 742938285, 950706376, 1226874159, 62089911, 1343714438} |
| 10. | SIMSCRIPT | LCG(231-1, 630360016,0,1) |
| 12. | Hoaling LCG's | LCG(231-1, a, 0, 1) a = {107831381, 1203248318, 397204094, 2027812808, 1323257245, 764261123} |
