Цели и задачи изучения темы
Целью данной темы является рассмотрение вопросов защиты информации криптографическими методами.
Принципы криптографической защиты информации
Криптография представляет собой совокупность методов преобразования данных, направленных на то, чтобы сделать эти данные бесполезными для злоумышленника. Применение криптографических методов позволяет обеспечить важнейшие свойства информации, такие как конфиденциальность,целостность,аутентичность и апеллируемость и решить ряд проблем информационной безопасности:
· проблему конфиденциальности – путем лишения злоумышленника возможности извлечь информацию из канала связи;
· проблему контроля целостности – путем лишения злоумышленника возможности скрытия факта изменения сообщения или ввода ложной информации в канал связи;
· проблему аутентификации – путем проверки подлинности субъектов информационных отношений или подлинности самой информации;
· проблему обеспечения невозможности отказа от обязательств – путем предотвращение возможности отказа субъектов от совершенных ими действий.
Базовыми методами криптографического преобразования информации являются:
· шифрование (симметричное и асимметричное);
· вычисление хэш-функций;
· генерация электронной цифровой подписи;
· генерация последовательности псевдослучайных чисел.
Система защиты информации, основанная на методах криптографии обычно называется криптографической системой, или более коротко – криптосистемой.
Шифры
Обеспечение конфиденциальности осуществляется с помощью методов шифрования. Обобщенная схема криптографической системы шифрования показана на рис. 2.1. Согласно этой схемы, отправитель генерирует открытый текст исходного сообщения М, которое должно быть передано законному получателю по незащищенному каналу. За каналом следит злоумышленник с целью перехватить и раскрыть передаваемое сообщение. Для того чтобы злоумышленник не смог узнать содержание сообщения М, отправитель шифрует его с помощью обратимого преобразования EK и получает шифртекст (или криптограмму) C=EK(M), который отправляет получателю.
Законный получатель, приняв криптограмму C, расшифровывает его с помощью обратного преобразования D=EK-1 и получает исходное сообщение в виде открытого текста М:
DK (C) = EK-1(EK(M)) = M.
|
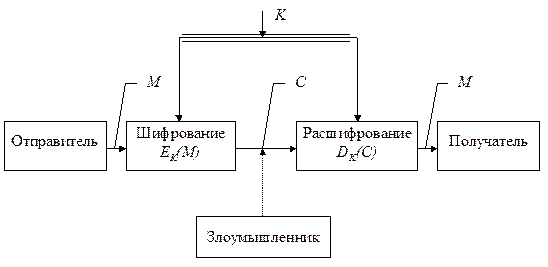
| Рис. 2.1. Обобщенная схема криптосистемы. |
Преобразование EK выбирается из семейства криптографических преобразований, называемых криптоалгоритмами. Параметр, с помощью которого выбирается отдельное используемое преобразование, называется криптографическим ключом K.
Таким образом, процесс преобразования открытого текста с целью сделать непонятным его смысл для посторонних называется шифрованием. В результате шифрования получается шифртекст. Процесс обратного преобразования шифртекста в открытый текст называется расшифрованием.
В соответствии со стандартом ГОСТ 28147-89 под шифром понимают совокупность обратимых преобразований множества открытых данных на множество зашифрованных данных, задаваемых ключом и алгоритмом криптографического преобразования.
Криптосистема имеет разные варианты реализации: набор инструкций, аппаратные средства, комплекс программ компьютера, которые позволяют зашифровать открытый текст и расшифровать шифртекст различными способами, один из которых выбирается с помощью конкретного ключа K.
Говоря более формально, криптографическая система – это однопараметрическое семейство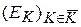 
обратимых преобразований
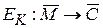
из пространства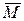 
сообщений открытого текста в пространство 
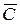шифрованных текстов. Параметр K (ключ) выбирается из конечного множества 
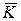, называемого пространством ключей.
Вообще говоря, преобразование шифрования может быть асимметричным относительно расшифрования. Это важное свойство функции преобразования определяет два класса криптосистем:
· симметричные (одноключевые) криптосистемы;
· асимметричные (двухключевые) криптосистемы (с открытым ключом).
Схема симметричной криптосистемы с одним секретным ключом была показана на рис. 2.1. В ней используются одинаковые секретные ключи в блоке шифрования и блоке расшифрования. В симметричной криптосистеме секретный ключ надо передавать отправителю и получателю по защищенному каналу распространения ключей, например такому, как курьерская служба. На рис. 2.1 этот канал показан "экранированной" линией.
Обобщенная схема асимметричной криптосистемы с двумя разными ключами K1 и K2 показана на рис. 2.2. В этой криптосистеме один из ключей является открытым, а другой – секретным. В асимметричной криптосистеме передают по незащищенному каналу только открытый ключ, а секретный ключ сохраняют на месте его генерации.
|
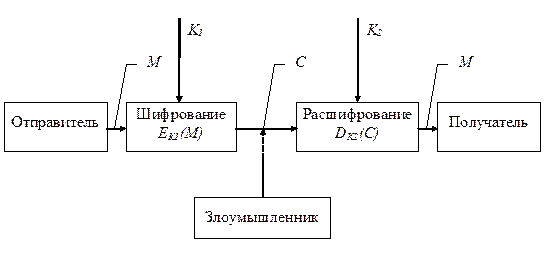
| Рис. 2.2. Обобщенная схема асимметричной криптосистемы с открытым ключом. |
В схеме на рис. 2.2 открытым ключом является K1, а секретным – K2. До начала передачи зашифрованного сообщения получатель формирует пару открытый ключ – секретный ключ (K1, K2) и передает получателю открытый ключ K1 по незащищенному каналу связи. Отправитель генерирует открытый текст M, выполняет шифрование C=EK1 (M) и передает криптограмму C получателю. Получатель осуществляет расшифрование M=DK2 (C) с помощью секретного ключа K2. Преобразование криптограммы в открытый текст возможно только при знании секретного ключа, который известен только получателю и, следовательно, злоумышленник оказывается не в состоянии получить открытый текст M даже, если ему удалось перехватить открытый ключ K1 и шифртекст C.
К шифрам, используемым для криптографической защиты информации, предъявляется ряд общепринятых требований:
· шифртекст должен поддаваться чтению только при наличии ключа;
· число операций, необходимых для определения использованного ключа шифрования по фрагменту шифртекста и соответствующего ему открытого текста, должно быть не меньше общего числа возможных ключей;
· число операций, необходимых для раскрытия шифра путем перебора всевозможных ключей должно иметь строгую нижнюю оценку и выходить за пределы возможностей современных компьютеров (с учетом возможности использования сетевых вычислений);
· знание алгоритма шифрования не должно влиять на надежность защиты;
· незначительное изменение ключа должно приводить к существенному изменению вида шифртекста;
· структурные элементы алгоритма шифрования должны быть неизменными;
· дополнительные биты, вводимые в сообщение в процессе шифрования, должен быть полностью и надежно скрыты в шифртексте;
· длина шифртекста должна быть равной длине открытого текста;
· не должно быть простых и легко устанавливаемых зависимостей между ключами, последовательно используемыми в процессе шифрования;
· любой ключ из множества возможных ключей должен обеспечивать надежную защиту информации;
· алгоритм должен допускать как программную, так и аппаратную реализацию.
Односторонние функции
Все асимметричные криптосистемы основаны на использовании односторонних функций с секретом.
Функция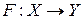 
называется односторонней, если выполняются следующие два условия:
1) существует эффективный алгоритм, вычисляющий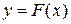 
для любого 
;
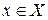2) не существует эффективного алгоритма обращения функции F, т.е. алгоритма, позволяющего определить значение x по значению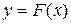 
.
В данном определении "эффективным" называется полиномиальный алгоритм, т.е. алгоритм, который для получения результата для входа длины n тратит не более P (n) шагов, где P – некоторый полином.
В настоящее время предложено несколько функций, которые могут оказаться односторонними, так как для них, несмотря на интенсивные исследования, не известны эффективные алгоритмы обращения. Наиболее часто используются "односторонние" функции, заимствованные из теории чисел:
· функция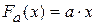 
, то есть произведение двух чисел. Если a и x – простые числа, то по известному 
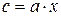можно однозначно определить a и x. Задача нахождения двух множителей по известному их произведению называется задачей факторизации числа. До сих пор не известен ни один полиномиальный алгоритм для решения задачи факторизации в общем случае (когда множители не являются простыми числами), хотя вычисление произведения чисел (т.е. самой функции F) не вызывает ни каких сложностей.
· функция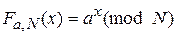 
, где a, x и N – целые числа. При известных a, x и N значение 
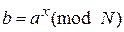может быть вычислено за полиномиальное количество шагов. Однако для обратной задачи – определить x по известным a, b и N (задача дискретного логарифмирования) – полиномиальные алгоритмы, в общем случае, пока не известны.
Не любая односторонняя функция не может быть использована для шифрования. Действительно, если преобразовать открытый текст M с помощью односторонней функции: C=F (M), то расшифровать полученный текст, то есть по C восстановить M, не сможет уже никто, в том числе и законный получатель. Для использования в криптографии необходимо, чтобы задача обращения шифрующего преобразования была разрешима за приемлемое время, но сделать это мог только тот, кто знает секретный ключ. Такие функции называются односторонними функциями с секретом (или с потайным ходом).
Односторонняя функция с секретом – это функция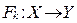 
, зависящая от параметра 
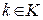(этот параметр называется секретом), для которой выполняются следующие условия:
1) при любом 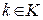существует эффективный алгоритм, вычисляющий 
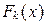для любого 
;
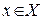2) при неизвестном k не существует эффективного алгоритма обращения функции 
;
3) при известном k существует эффективный алгоритм обращения функции .
В настоящее время известны функции, которые могут оказаться односторонними функциями с секретом, если будет доказано, что инвертирование этих функций без знания секрета действительно является сложной задачей.
Хэш-функции
Хэш-функция – это вычислительно эффективная функция h:P ® S, отображающая двоичную строку произвольной длины p Î P, называемую прообразом в двоичную строку некоторой фиксированной длины s = h (p), где sÎS, называемую хэш-значением. Здесь P – множество прообразов (счетное множество двоичных строк произвольной длины), S – конечное множество хэш-значений.
В качестве простой хэш-функции можно рассматривать функцию, которая получает прообраз в виде строки и возвращает байт, представляющий собой XOR всех входных байтов или функцию вычисления циклического избыточного кода.
Смысл хэш-функции состоит в получении характерного признака прообраза s = h (p)– значения, по которому анализируются различные прообразы при решении обратной задачи p = h –1(s). Так как хэш-функция представляет собой соотношение "многие к одному" (существуют различные прообразы, имеющие одинаковые хэш-значения), невозможно со всей определенностью сказать, что две строки совпадают при совпадении хэш-значений, но их можно использовать, получая приемлемую оценку точности.
Однонаправленная или криптографическая хэш-функция – это хэш-функция, удовлетворяющая следующим свойствам:
1) существует эффективный алгоритм нахождения s = h (p)для любого p (легко вычислить значение хэш-функции по прообразу);
2) не существует эффективного алгоритма обращения функции h, то есть вычислительно сложно найти p = h –1(s) (трудно создать прообраз, значение хэш-функции которого равно заданной величине);
3) зная прообраз p трудно определить другой прообраз p', для которого h (p) = h (p').
Упоминавшиеся ранее хэш-функции, вообще говоря, не являются однонаправленными, например, задав конкретный байт, не представляет труда создать строку байтов, XOR которых дает заданное значение.
Кроме этого, хорошей однонаправленной хэш-функцией считается хэш-функция c малой вероятностью возникновения коллизий –трудно подобрать два прообраза p и p' с одинаковым хэш-значением h (p) = h (p').
В криптографических приложениях у однонаправленной хэш-функции может быть множество имен, например, функция сжатия или функция сокращения. Хэш-значения, также могут называться по-разному: краткое изложение сообщения (message digest, MD), характерный признак, криптографическая контрольная сумма, код целостности сообщения (message integrity check, MIC) и код обнаружения манипуляции (manipulation detection code, MDC). Последние два названия отражают возможность применения хэш-функции для обеспечения целостности информации.
Хэш-функции могут быть использованы для обеспечения целостности следующим образом. В определенный момент времени вычисляется хэш-значение, соответствующее конкретным входным данным. Некоторым образом обеспечивается целостность этого хэш-значения. В дальнейшем для проверки того, что входные данные не были изменены, хэш-значение перерассчитывается и сравнивается на равенство с оригинальным хэш-значением.
Обычно, хэш-функция является открытой, то есть тайны ее расчета не существует. Безопасность однонаправленной хэш-функцией заключается именно в ее однонаправленности. У выхода нет видимой зависимости от входа. Изменение одного бита прообраза приводи к изменению в среднем половины битов значения хэш-функции. Вычислительно невозможно найти прообраз, соответствующий заданному значению хэш-функции.
С другой стороны, имеются хэш-функции, предполагающие использование секретного ключа и обеспечивающие как аутентификацию источника сообщения, так и целостность данных. Значения таких хэш-функций называются кодами аутентификации сообщения (message authentication code, MAC).
Простым способом преобразовать результат однонаправленной хэш-функции в MAC является шифрование хэш-значения симметричным алгоритмом.
Основное отличие МАС от других хэш-значений заключается в том, что при его создании источник сообщения использует некоторую секретную информацию – ключ, знание которого идентифицирует этот источник. При этом только владелец идентичного ключа может перерассчитать хэш-значение сообщения и, если целостность не была нарушена, получить совпадение с оригинальным кодом. Это означает, что подделать MAC при изменении сообщения могут только те субъекты, которые знают ключ.
Например, MAC могут быть использованы для проверки подлинности файлов, которыми обмениваются пользователи. Также они могут быть использованы одним пользователем для проверки, не изменились ли его файлы, может быть из-за вируса. Пользователь может вычислить MAC его файлов и сохранить эти значения в таблице. Если пользователь воспользуется вместо MAC однонаправленной хэш-функцией, то вирус может вычислить новые хэш-значения после заражения файлов и заменить элементы таблицы.
С MAC вирус не сможет этого добиться, так как ключ вирусу неизвестен.
Следует отметить, что в отношении хэш-функций, предполагающих использование секретного ключа, в России используются несколько иные термины, такие как имитовставка и имитозащита. Так, в соответствии со стандартом ГОСТ 28147-89, имитовставка – это хэш-значение сообщения, который вырабатывают по определенному правилу из открытых данных с использованием ключа и затем добавляют к зашифрованным данным для обеспечения их имитозащиты. Имитозащита – это защита системы шифрованной связи от навязывания ложных данных.
