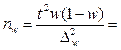Задача 1. Для определение средних затрат рабочего времени на 1 ц продукции растениеводства была проведена 5% выборка в которую попало 35 хозяйств специализированных на производство зерна. Установлено, что средние затраты труда на производство 1 ц продукции составляют 14,8 чел.-ч, при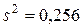 
Необходимо определить среднюю и предельную (с вероятностью 0,954 (при 
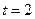)) ошибку выборки для случайного бесповторного отбора, повторить для случайного повторного отбора.
Решение.
Средняя ошибка выборочной средней при случайном бесповторном отборе:
При бесповторном отборе предельная ошибка выборочной средней определяется как:
То есть, с вероятностью 0,954, можно сказать, что средние затраты рабочего времени на 1 ц продукции растениеводства находятся в пределах 
.
Средняя ошибка при случайном повторном отборе выборочной средней рассчитывается по формуле:
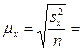
При повторном отборе предельная ошибка выборочной средней определяется как:
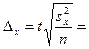
То есть, с вероятностью 0,954, можно сказать, что средние затраты рабочего времени на 1 ц продукции растениеводства находятся в пределах 
.
Расчет по бесповторной модели всегда точнее.
Задача 2. Методом бесповторного отбора из общей численности молочного стада была проведена 5% выборка в которую попало 200 голов. Результаты показали, что 30% коров в выборке старше 5 лет. Определить с вероятностью 0,7699 пределы, в которых находится доля коров старше 5 лет, дисперсия доли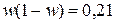 
Решение.
Средняя ошибка выборочной доли определяется:
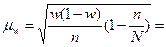
При бесповторном отборе предельная ошибка для выборочной доли определяется как:
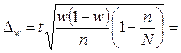
То есть, с вероятностью 0,7699 можно утверждать, что доля коров старше 5 лет составляет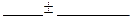 
.
Задача 3. Молочное стадо крупного рогатого скота в районе составляет 15000 голов. Необходимо определить численность выборки, в которой с вероятностью 0,9109 предельная ошибка среднего надоя не должна превышать 0,2 кг при среднем квадратическом отклонении надоя 1,2 кг.
Решение. Численность выборки при бесповторном отборе определяется как:
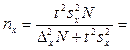
Проведем проверку:
Средняя ошибка:
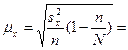
Предельная ошибка выборочной средней при вероятности 0,9109 (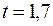
) 
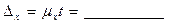что не превышает заданной ошибки предельной ошибки 0,2 кг.
Задача 4. В районе среди 11000 частных индивидуальных хозяйств изучается доля хозяйств с числом голов крупного рогатого скота две и более на одно хозяйства.
Необходимо определить необходимую численность выборки для бесповторного и повторного отборов с вероятностью 0,6827(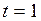
) и ошибкой выборки доли хозяйств, с числом голов три и более, не превышающей 0,03, известно, что дисперсия равна 0,4.
Решение.
1. Для бесповторного отбора
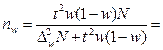
2. Для повторного отбора
