Задачи для подготовки к экзамену по математике
Менеджеры 2011/2012
1. Найти интегралы: а) 
; б) 
; в) 
; г) 
.
2. Вычислить несобственный интеграл 
или установить его расходимость.
3. Вычислить площадь фигуры, ограниченной линиям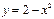и 
и 
.
4. Вычислить площадь фигуры, ограниченной линиями 
, 
, 
и 
.
5. Хоккейная команда состоит из 2 вратарей, 7 защитников и 10 нападающих. Сколькими способами тренер может составить стартовую шестерку, состоящую из вратаря, двух защитников и трех нападающих?
6. Комната освещается 4 лампочками, каждая их которых включается независимо от других. Сколькими различными способами можно осветить комнату?
7. Студент подготовил к экзамену 50 вопросов из 60. Какова вероятность того, что во взятом наугад билете оба вопроса будут из числа подготовленных?
8. Два охотника стреляют в волка, причем каждый делает по одному выстрелу. Для первого охотника вероятность попадания в цель равна 0,7, а для второго - 0,8. Какова вероятность попадания в волка хотя бы одним стрелком?
9. Случайная величина Х распределена равномерно на отрезке [0;6]. Найти функцию распределения, математическое ожидание и среднее квадратическое отклонение Х.
10. Функция распределения непрерывной случайной величины имеет вид 
. Найти функцию плотности вероятности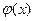 
. Чему равна вероятность того, что случайная величина примет значение из интервала 
?
11. Аудиторную работу по теории вероятностей с первого раза успешно выполняют 60 % студентов. В первом потоке контрольную работу написали 100 человек. Найти вероятность того, что успешных работ будет от 30 до 70.
12. Коробки с мармеладом упаковываются автоматически. Их средняя масса равна 900 г. Известно, что 1% коробок имеют массу, большую 1 кг. Каков % коробок, масса которых не превышает 850 г., если вес коробок - случайная величина, распределенная по нормальному закону
13. Литье в болванках поступает на обработку из 2 цехов: 70% из первого и 30% из второго. Процент брака в первом цехе равен 10%, во втором - 20%. Наудачу взятая болванка не имеет дефектов. Найти вероятность того, что она из первого цеха.
14. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента 0,1. Составить закон распределения числа оказавших элементов. Найти математическое ожидание и дисперсию этой случайной величины.
15. Диаметр детали, изготавливаемой на станке, - случайная величина, распределенная по нормальному закону с математическим ожиданием 25 см. и средним квадратическим отклонением 0,4 см. Найти вероятность того, что наудачу взятая деталь имеет отклонение от математического ожидания по абсолютной величине не более 0,16 см.
16. По результатам измерений 21, 27, 27, 22, 23, 22, 25, 25, 24, 26, 23, 24, 23, 35, 26, 26, 25, 25, 24, 24, 22, 23, 21, 21, 22 построить дискретный статистический ряд, полигон относительных частот. Найти несмещенную оценку математического ожидания и доверительный интервал для математического ожидания с надежностью 0,95, если предположить, что генеральная совокупность имеет нормальное распределение с квадратическим отклонением 
.
17. По статистической выборке
| x | |||||
| n |
найти доверительный интервал с надежностью 0,9 для оценки среднего квадратического отклонения нормально распределенной генеральной совокупности.
18. При уровне значимости 0,1 и альтернативной гипотезе 
проверить гипотезу о равенстве дисперсий двух нормально распределенных случайных величин X и Y на основе выборочных данных: 
; 
; 
; 
.
19. На основании полученных измерений величин Х и Y
| X | |||||
| Y |
Найти уравнение регрессии Y на X и выборочный коэффициент корреляции. Сделать вывод о связи между величинами.
ВНИМАНИЕ! Задачи по теме «Интегрирование» Вы можете взять в любом количестве из практикума Кремера.
