Графы!
Вводное.
Что это вообще такое? На данном этапе граф можно и нужно воспринимать как некоторое обобщение различных объектов, которые можно изобразить, обозначив что-то за точки, а что-то – за линии, их соединяющие. Например, города и дороги между ними (город – точка, дорога - линия), или знакомства между людьми (человек – точка, знакомство – линия; если люди не знакомы, линии между ними нет).
- Напишите по кругу числа от 1 до 15. А потом соедините линией те пары, где большее число делится на меньшее. У вас получится граф.
- Теперь напишите названия всех дней недели (понедельник, вторник, …, воскресенье). Соедините названия линиями, если они имеют общую букву. Теперь напишите заново и соедините, если букв хотя бы две.
- Придумайте свой граф – объекты и то, что соединяет некоторые из них.
Суть вы поняли! Кстати, карта метро – уже готовый граф.
Основные понятия, которые нам нужны.
Вершины графа – это те самые точки, которые мы соединяем. Города, числа, люди и так далее.
Ребра графа – линии, соединяющие точки. Дороги между городами, рукопожатия между людьми, делимость между числами и так далее.
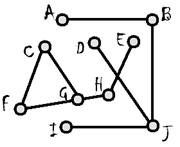
Степень вершины – число ребер, выходящих из нее. Например, в графе, который нарисован справа, вершины A, I, E и D имеют степень 1, потому что из них выходит всего по одному ребру, вершины B, H, F и С имеют степень 2, а вершины G и J имеют степень 3.
Если в графе всего N вершин, то максимальная степень вершины в нем может быть равна N-1 – когда одна вершина соединена со всеми остальными. Минимальная, разумеется, может быть равна 0.
Путь в графе – последовательность вершин, в которой любые две соседние вершины соединены между собой ребром. На данной картинке, например, A B J I – путь.
Цикл в графе – путь, у которого первая вершина совпадает с последней. На картинке – C G F C.
Связный граф – граф, в котором от любой до любой другой существует путь (то есть можно «дойти» по ребрам). Например, граф справа не связный, ведь от A до E, например, не добраться.
1) Нарисуйте граф с 6 вершинами и степенями вершин 2,2,3,3,4,4
2) Попробуйте нарисовать граф с 7 вершинами и степенями 6,6,4,4,2,1,1. Почему не получается?
Основное соображение.
Давайте посчитаем количество ребер в графе. Делать это будем так – сложим все степени вершин, ведь так мы как раз подсчитаем все ребра. Если из вершины А выходит три ребра, из вершины Б – два, из вершины В - тоже два, из вершины Г – одно, то сумма 3+2+2+1=8 должна учитывать все ребра.
Но! Поскольку каждое ребро выходит ровно из двух вершин, мы и учли его дважды. Например, ребро между А и Б мы подсчитали и в степени А, и в степени Б. Следовательно, наше полученное число следует еще разделить пополам, и тогда мы получим реальное количество ребер. То есть
Сумма степеней всех вершин в графе равна удвоенному количеству ребер в нем!
- Проверьте это на графах, которые вы уже нарисовали – подсчитайте сумму степеней и количество ребер. Убедитесь в том, что это правило работает и запомните его навсегда.
Приятное следствие: сумма степеней вершин графа всегда четна. Потому что она равна удвоенному числу ребер. И этим тоже следует активно пользоваться.
Примеры того, как помогают решать задачи эти соображения.
Пример №1: Могут ли все вершины в графе иметь степень 2, а одна вершина – степень 3?
Ответ: Нет, не могут. Сумма степеней – какое-то количество двоек и одна тройка – безусловно нечетна. А она не может быть нечетной, потому что равна удвоенному количеству ребер.
Пример №2: В графе сто вершин и а) каждая соединена с каждой; б) у каждой степень равна 50; в) степень 25 из них равна 4, 25 – 8, а у 50 – 6. Сколько ребер в графе?
Ответ: Просто считаем сумму степеней и делим пополам. В первом случае это (100*99):2 = 4950, во втором - (100*50):2=2500, в третьем – (25*4+25*8+50*6):2=300.
В нижеследующих задачах очень важно «найти граф» - определить какие-то объекты как вершины, а какие-то – как ребра.
Решите это сами:
3) Известно, что в графе все степени вершин равны, самих вершин 24, а ребер – 60. Чему равна степень любой вершины этого графа?
4) Докажите, что в любом графе какие-то две вершины имеют одинаковую степень.
5*) В компании из k человек каждый имеет ровно трех знакомых, любые двое незнакомых имеют общего знакомого и есть трое попарно знакомых. Найдите наибольшее возможное значение k.
6) В стране есть несколько аэропортов, каждый из которых соединён авиалиниями ровно с пятью другими. Однажды из-за сильного снегопада бóльшую часть аэропортов пришлось закрыть. После этого оказалось, что из каждого работающего аэропорта можно вылететь только в три других, а закрытыми оказались 26 авиалиний. (Авиалиния закрывается, если закрывается хотя бы один из двух аэропортов, которые она соединяет.)
а) Докажите, что число работающих после снегопада аэропортов чётно.
б*) Докажите, что число закрывшихся аэропортов делится на 4.
в*) Сколько авиалиний не закрылось из-за снегопада?
Делимость и остатки.
С остатками все просто. Любое натуральное число от деления на любое другое дает какой-то остаток (иногда этот остаток равен 0, и тогда мы говорим, что одно число делится на другое). Например, 10 дает остаток 1 от деления на 3 и остаток 2 от деления на 8. И, к слову, оно же дает остаток 10 от деления на 11, 25, 26, 100, 413… и так далее. В общем, на любое число, которое больше, чем оно само.
