Курсовая работа по дисциплине
«Основы теории управления»
Динамический расчет системы автоматического управления скорости вращения оптического диска
(CD-ROM)
Вариант 10
студентки группы АК4-51
Саблиной Яны Юрьевны
_______________________
Руководитель ___________________ (Зуев Андрей Григорьевич)
Москва, 2009г.
Техническое задание.
1. Первая часть.
1.1. Сформировать функциональную блок-схему системы автоматического регулирования с вариантом задания и дать краткое описание принципа ее функционирования.
1.2. Пренебрегая нелинейностями характеристик функциональных элементов системы и дискретным характером процессов в отдельных точках системы, сформировать линейный модели элементов ее неизменяемой части и вычислить числовые значения параметров этих модулей с учетом варианта задания.
1.3. Определить передаточные функции элементов системы.
1.4. Составить структурную схему системы с учетом управляющего воздействия.
1.5. Методом структурных преобразований привести исходную структурную схему системы к эквивалентной с единичной обратной связью.
1.6. Определить передаточные функции системы:
a) Передаточную функцию разомкнутой системы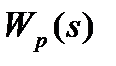 
;
b) Передаточную функцию замкнутой системы 
;
c) Передаточную функцию ошибки 
по управляющему воздействию.
1.7. Построить дифференциальные уравнения системы в разомкнутом и замкнутом состояниях.
1.8. Получить выражения характеристических полином для системы в разомкнутом и замкнутом состояниях.
1.9. Проанализировать устойчивость системы, используя алгебраический критерий Гурвица и частотный критерий Найквиста.
1.10.Определить показатели динамического качества и статической точности по реакциям системы на тестовые ступенчатое и линейно возрастающее входное воздействие. Сопоставить полученные в результате исследований значения показателей качества и статической точности с заданными и сделать вывод о необходимости изменения структуры регулятора или использования динамической коррекции.
2. Вторая часть.
2.1. Основываясь на результатах статического расчета показать, что заданная точность позиционирования ОГ может быть достигнута с использованием пропорционального закона регулирования.
2.2. Исходя из требуемой статической точности системы определить параметр 
пропорционального закона регулирования, передаточная функция 
2.3. Исходя из условий обеспечения требуемых значений прямых показателей динамического качества и показателей грубости системы определить корректирующий фильтр заданной структуру вида: 
, где T – искомый параметр фильтра.
2.4. Решить задачу анализа устойчивости системы с учетом результатов параметрического синтеза регулятора и динамических корректирующий фильтров с использованием частотного критерия Найквиста, получить оценки запасов устойчивости по фазе и амплитуде. Сравнить полученные результаты с заданными.
2.5. Решить задачу анализа статической точности и динамического качества, определить 
и 
. Сравнить полученные результаты с заданными.
Вариант 10.
Тип системы – В – система автоматического регулирования скорости вращения оптического диска.
Условия для выполнения:
| Вар | Таходатчик | ЦАП | Предусилитель | Усилитель мощности | Двигатель шпинделя | 
| |||||
 m
| Nтд | Um | Nцап | Ку | Тум | Кум | Кдв | Тдв | m
| εm | |
| об/мин | ед | В | ед | ед | с | ед | 1/сВ | с | 1/с2 | 1/c | |
| 1.4 | .005 | 9.5 | .015 | 0.1 | 0.002 |
Сформировать функциональную блок-схему системы автоматического регулирования с вариантом задания и дать краткое описание принципа ее функционирования.
Контур автоматического управления и стабилизации угловой скорости вращения шпинделя оптического диска включает:
- привод шпинделя на основе двигателя постоянного тока;
- цифровой датчик угловой скорости вращения шпинделя (таходатчик);
- цифро-аналоговый преобразователь (ЦАП);
- усилитель мощности напряжения постоянного тока;
-редуктор, усиливающий угловую скорость
- цифровой контроллер, реализующего алгоритмы обработки информации.
Пренебрегая нелинейностями характеристик функциональных элементов системы и дискретным характером процессов в отдельных точках системы, сформировать линейный модели элементов ее неизменяемой части и вычислить числовые значения параметров этих модулей с учетом варианта задания.
(Без учёта нелинейностей и дискретного характера процессов)
Математическая модель предварительного усилителя:
ɛ
У
У
U
K
U
×
где: =
;
Математическая модель усилителя мощности.
Математическая модель двигателя:
; 
Где: 
, 
Математическая модель таходатчика:
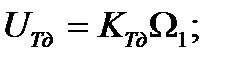
где: 
Математическое описание редуктора
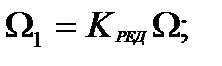
Определить передаточные функции элементов системы.
1. Передаточная функция предварительного усилителя
2. Передаточная функция усилителя
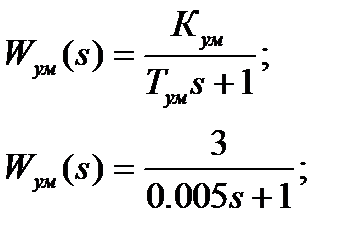
3. Передаточная функция двигателя
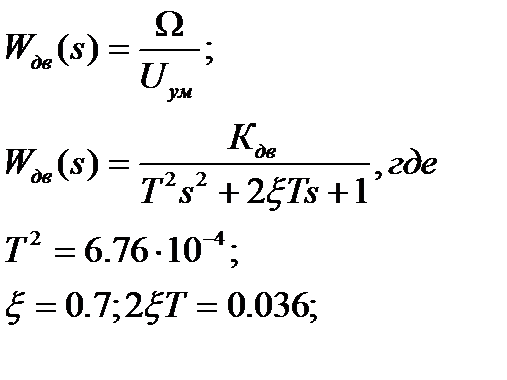
4. Передаточная функция таходатчика
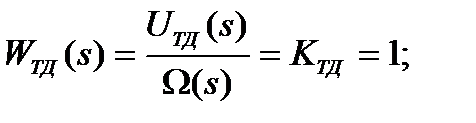
5. Передаточная функция редуктора
