I. 1. 
2. 
3. 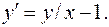
4. 
5. 
6.  ctg
ctg 
7. 
II. 8. 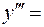 tg
tg  Вычислить
Вычислить 
9. 
10. 
III.11. 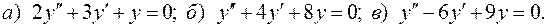
12. 
13. 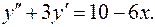
14. 
15. Определить и записать структуру частного решения  ЛНДУ по виду функции f(x).
ЛНДУ по виду функции f(x).
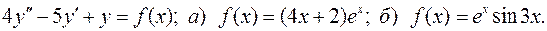
IV.16. Решить систему дифференциальных уравнений

V. 17. Записать уравнение кривой, проходящей через точку А(-1, 3), если известно, что угловой коэффициент касательной в любой её точке равняется ординате этой точки, увеличенной в 2 раза.
Вариант 15
Найти общие или частные решения дифференциальных уравнений.
I. 1. 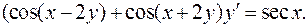
2. 
3. 
4. 
5. 
6. 
7. 
II.8.  Вычислить
Вычислить 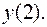
9.  tg
tg 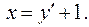
10. 
III.11. 
12. 
13. 
14. 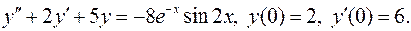
15. Определить и записать структуру частного решения  ЛНДУ по виду функции f(x).
ЛНДУ по виду функции f(x).
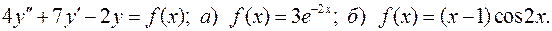
IV.16. Решить систему дифференциальных уравнений

V. 17. Сила сопротивления воздуха при падении тела с парашютом пропорциональна квадрату скорости движения. Найти предельную скорость падения тела.
Вариант 16
Найти общие или частные решения дифференциальных уравнений.
I. 1. 
2. 
3. 
4. 
5. 
6. 
7. 
II.8. 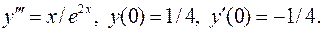 Вычислить
Вычислить 
9. 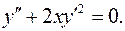
10. 
III.11. 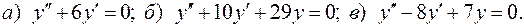
12. 
13. 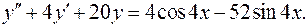
14. 
15. Определить и записать структуру частного решения  ЛНДУ по виду функции f(x).
ЛНДУ по виду функции f(x).

IV.16. Решить систему дифференциальных уравнений

V. 17. Записать уравнение кривой, проходящей через точку А(3,-1), если известно, что угловой коэффициент касательной в любой её точке в 3/2 раз больше углового коэффициента прямой, соединяющей ту же точку с началом координат.
Вариант 17
Найти общие или частные решения дифференциальных уравнений.
I. 1. ctg  tg
tg 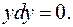
2. 
3. 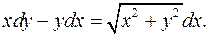
4. 
5. 
6. 
7. 
II.8. 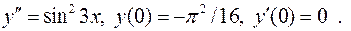 Вычислить
Вычислить 
9. 
10. 
III.11. 
12. 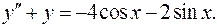
13. 
14. 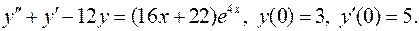
15. Определить и записать структуру частного решения  ЛНДУ по виду функции f(x).
ЛНДУ по виду функции f(x).
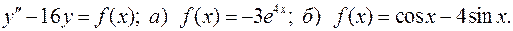
IV.16. Решить систему дифференциальных уравнений

V. 17. Ускорение локомотива прямо пропорционально силе тяги F и обратно пропорционально массе поезда m. Начальная скорость локомотива  , сила тяги
, сила тяги  – скорость;
– скорость;  – постоянные величины. Найти силу тяги локомотива как функцию времени t, если в начальный момент t = 0
– постоянные величины. Найти силу тяги локомотива как функцию времени t, если в начальный момент t = 0  .
.
Вариант 18
Найти общие или частные решения дифференциальных уравнений.
I. 1. 
2. 
3. 
4. 
5. 
6. 
7. 
II. 8. 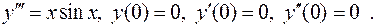 Вычислить
Вычислить 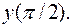
9. 
10. 
III.11. 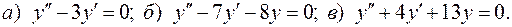
12. 
13. 
14. 
15. Определить и записать структуру частного решения  ЛНДУ по виду функции f(x).
ЛНДУ по виду функции f(x).

IV.16. Решить систему дифференциальных уравнений

V. 17. Записать уравнение кривой, проходящей через точку А(0,-8), если известно, что длина отрезка, отсекаемого на оси ординат нормалью, проведённой в любой точке кривой, равна расстоянию от этой точки до начала координат.
Вариант 19
Найти общие или частные решения дифференциальных уравнений.
I. 1. 
2. 
3. 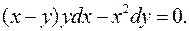
4. 
5. 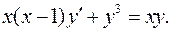
6. 
7. 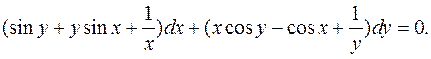
II. 8.  Вычислить
Вычислить 
9.  tg
tg 
10. 
III.11. 
12. 
13. 
14. 
15. Определить и записать структуру частного решения  ЛНДУ по виду функции f(x).
ЛНДУ по виду функции f(x).
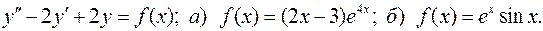
IV.16. Решить систему дифференциальных уравнений

V. 17. Интенсивность света, проходящего через слой воды, уменьшается пропорционально интенсивности падающего света и толщине слоя. Если при прохождении слоя воды толщиной 3 м интенсивность света уменьшается вдвое, то какова будет интенсивность на глубине 30 м?
Вариант 20
Найти общие или частные решения дифференциальных уравнений.
I. 1.  ctg
ctg 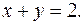
2. 
3. 
4. 
5. 
6. 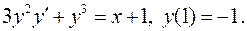
7. 
II. 8.  Вычислить
Вычислить 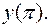
9.  ctg
ctg 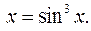
10. 
III.11. 
12. 
13. 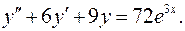
14. 
15. Определить и записать структуру частного решения  ЛНДУ по виду функции f(x).
ЛНДУ по виду функции f(x).
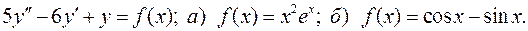
IV.16. Решить систему дифференциальных уравнений

V.17. Записать уравнение кривой, проходящей через точку А(-2, 5) и обладающей следующим свойством: отрезок, который касательная в любой точке кривой отсекает на оси Оу, равен квадрату абсциссы точки касания.
Вариант 21
Найти общие или частные решения дифференциальных уравнений.
I. 1. 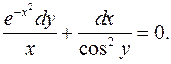
2. 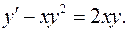
3. 
4. 
5. 
6. 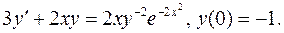
7. 
II. 8.  Вычислить
Вычислить 
9. 
10. 
III.11. 
12. 
13. 
14. 
15. Определить и записать структуру частного решения  ЛНДУ по виду функции f(x).
ЛНДУ по виду функции f(x).

IV.16. Решить систему дифференциальных уравнений
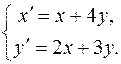
V. 17. На тело массы  , движущееся в вязкой среде со скоростью
, движущееся в вязкой среде со скоростью  , действует сила сопротивления
, действует сила сопротивления  Начальная скорость тела
Начальная скорость тела  м/с. Через 2 с его скорость уменьшается до 3 м/с. За какое время тело пройдёт путь в 5 м?
м/с. Через 2 с его скорость уменьшается до 3 м/с. За какое время тело пройдёт путь в 5 м?
Вариант 22
Найти общие или частные решения дифференциальных уравнений.
I. 1.  tg
tg 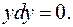
2. 
3. 
4. 
5. 
6. 
7. 
II.8.  Вычислить
Вычислить 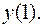
9. 
10. 
III.11. 
12. 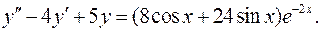
13. 
14. 
15. Определить и записать структуру частного решения  ЛНДУ по виду функции f(x).
ЛНДУ по виду функции f(x).

IV.16. Решить систему дифференциальных уравнений

V. 17. Записать уравнение кривой, проходящей через точку А(-2, 5) и обладающей следующим свойством: длина перпендикуляра, опущенного из начала координат на касательную к кривой, равна абсциссе точки касания.
Вариант 23






