Лабораторная работа 1-м
Исследование движения газовой среды в трубах переменного сечения.
Выполнил:
студент группы Мт-37051
Сумин А.Д.
Проверил:
Шаврин В.С.
Екатеринбург
Г
Лабораторная работа 1-м.
Исследование движения газовой среды в трубах переменного сечения.
1 Цель работы:
Изучение закономерностей изменения давления при движении сплошной среды в канале переменного сечения на примере движения воздуха в трубе Вентури.
Описание лабораторной установки и принцип ее работы
Лабораторная установка для изучения закономерностей движения газов по трубам и каналам показана на рисунке 1. Таких установок в лаборатории установлено 3 и ко всем установкам, централизовано, подведён воздух от одного вентилятора. (Вентилятор включает только преподаватель). На каждой установке работает одна бригада студентов.
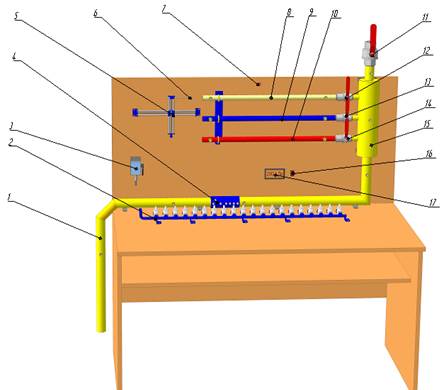
Рисунок 1 – Лабораторная установка
1 – воздуховод; 2 – коллектор с кнопочными кранами; 3 – датчик давления; 4 – труба Вентури; 5 – координатник; 6 – измерительная пневмометрическая трубка; 7 – сигнальная лампочка; 8 – гладкая труба с внутренним диаметром 20 мм; 9 – труба с абсолютной шероховатостью 0,3 мм; 10 – труба с абсолютной шероховатостью 0,6 мм; 11 – шаровой кран диаметром 40 мм; 12, 13, 14 – шаровые краны диаметром 20 мм; 16 – электрический выключатель; 17 – вторичный прибор измерения давления.
2. Общие сведения
Уравнение Бернулли является одним из основных уравнений гидродинамики. Если не учитывать процессов рассеянья энергии, которые могут иметь место в текущей непрерывной среде вследствие внутреннего трения и теплообмена между различными ее участками, т. е. рассматривать течение идеальной среды, то для несжимаемой среды постоянной плотности уравнение Бернулли имеет вид
gh + Р/ρ+w2/2= const,
где g - ускорение свободного падения; h - высота относительно горизонтальной плоскости сравнения.
Как раз для этого случая это уравнение и было выведено Даниилом Бернулли в 1738 году. Если уравнение (4) умножить на плотность р, то получим выражение
ρgh + P + (w2/2)*ρ= const,
где первые два слагаемых представляют собой выражение потенциальной энергии, часть которой обусловлена внешними силами, другая часть -давлением Р; третье слагаемое уравнения выражает кинетическую энергию.
Следовательно, уравнение Бернулли, записанное в виде выражения (5), представляет собой не что иное, как закон сохранения энергии.
Уравнение Бернулли имеет большое значение в гидравлике, аэродинамике и механике газов: его используют при расчётах каналов и трубопроводов, вентиляторов и насосов, в вопросах, связанных с фильтрацией и т. п.
Пользуясь уравнением Бернулли, необходимо иметь в виду, что оно получено без учета сил трения, и поэтому, применяя его к реальной среде (жидкости или газу), необходимо учитывать потери энергии на соответствующие местные сопротивления и трение, которые имеют место при течении сред в трубах и каналах.
Все описанные выше явления наблюдаются при движении воздуха в трубах переменного сечения. Характерным примером трубы с плавно изменяющимся сечением является труба Вентури. Профиль трубы Вентури представляет собой постепенное сужение (конфузор), плавно переходящее в расширение (диффузор). Опыт показывает, что с энергетической точки зрения постепенное сужение трубы влечёт за собой незначительную потерю энергии давления. И наоборот, при постепенном расширении потока возникают благоприятные условия для его отрыва от стенок. Надо иметь в виду, что восстановление статического давления по сечению потока, связанное с расширением трубы, всегда более полно при постепенном расширении, чем при внезапном, и зависит от угла раскрытия диффузора, поэтому угол раскрытия диффузора всегда стараются выполнить близким к оптимальному значению.
Труба Вентури служит характерным примером, иллюстрирующим переход давления одного вида в другой. Этот переход описывается уравнением Бернулли (5), которое показывает, что при отсутствии потерь сумма энергий движущейся среды в сечении II равна сумме энергий в сечении IV.
3 Порядок проведения работы
Перед началом работы ознакомиться с разделом «описание лабораторной установки».
3.1 Установить с помощью шарового крана 11 (см. рисунок 1.1) расход воздуха V1, при котором проводится эксперимент (рассчитывается студентом по перепаду давлений на трубе Вентури).
3.2 Произвести измерения статического давления (Pст) последовательно в каждом из восьми сечений, включая давление в точке 2. Произвести повторные измерения в обратном порядке, что позволит уменьшить возможные ошибки. Усреднённые результаты измерений занести в таблицу 1.1.
3.4 Рассчитать скорость потока во всех сечениях по формуле:
Wi =  . (9)
. (9)
где di – диаметр трубы в данном сечении, м.
3.5 Рассчитать динамическое давление, Па, в тех же сечениях по формуле:
 . (10)
. (10)
3.6 Рассчитать полное давление во всех сечениях по формуле:
Р Σ= Р ст+ Р дин. (11)
По полученным результатам измерений и расчётов, сведённым в таблицу 1.1, построить графические зависимость изменения статического и динамического давлений по длине экспериментального участка трубопровода, выполненного в виде трубы Вентури.
Ход работы.


W7 = 
W8 = 
W9 = 
W10 = 
W11 = 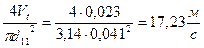
W12 = 
W13 = 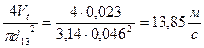
W14 = 

| Параметры | обозначение | |||||||||
| Расход | Vt | 0,023 | 0,023 | 0,023 | 0,023 | 0,023 | 0,023 | 0,023 | 0,023 | 0,023 |
| Диаметр | d | 0,044 | 0,04 | 0,037 | 0,038 | 0,041 | 0,044 | 0,046 | 0,048 | 0,05 |
| Скорость | Wi | 15,13 | 18,31 | 21,40 | 20,29 | 17,43 | 15,13 | 13,85 | 12,72 | 11,72 |
| Статическое давление | Pст | |||||||||
| Динамическое давление | Pдин | 132,84 | 194,49 | 265,67 | 238,79 | 176,20 | 132,84 | 111,20 | 93,79 | 80,9 |
| Полное давление | P∑ | 732,84 | 744,49 | 735,67 | 723,79 | 716,20 | 697,84 | 696,20 | 693,79 | 710,9 |
| Потеренное давление | ∆P | -11,65 | -8,82 | -11,88 | -7,59 | -18,36 | -1,64 | -2,41 | 17,11 |
График в виде эпюры давлений необходимо строить следующим образом: по оси абсцисс, которая одновременно является линией атмосферного давления, отложить длину экспериментального участка с отметками сечений, в которых был произведён замер статического давления, а по оси ординат отложить значения статического Р ст, динамического Р дин и полного Р Σ давлений. Падение полного давления по длине канала будет характеризовать потери, величина которых должна возрастать в направлении движения потока.

| t | температура | |
| P | давление по прибору | |
| p | 1,178 | плотность расчетная |
| V | 0,023 | расход по 3 и 9 точке |
| Вентилятор: | К Па | |
| t | ||
| P | ||
| об |
Вывод:
В данной лабораторной работе было изучено движение газов в трубе переменного сечения на примере трубы Вентури. При постепенном расширении канала возникают условия для отрыва потока от стенок. Р зависит от угла раскрытия, что показано на графике. Суммарное давление в начале возрастает и после точки 3 начинает падать. Это может быть связано с некачественными сварочными швами в точках 1 и 2.




