Тема 1. «статический расчет горной

СТАТИЧЕСКИЙ И ТЯГОВЫЙ РАСЧЕТ

ГОРНОЙ ГУСЕНИЧНОЙ МАШИНЫ

 

УЧЕБНОЕ ПОСОБИЕ

по курсам

«Машины и комплексы открытых горных работ» и

«Горные машины»

для студентов специальности 1-36 10 01

«Горные машины и оборудование»

 

Минск 2004

 

УДК 622.331.002

 

Учебное пособие к практическим занятиям по горным машинам предназначено для студентов специальности 1-36 10 01 «Горные машины и оборудование».

В пособии изложены теоретические основы и методики статического и тягового расчетов мобильной горной машины на гусеничном ходу. Изложенный материал иллюстрируется примерами.

 

Георгий Васильевич Казаченко

Николай Владимирович Кислов

 

Рецензенты:

Докт. техн. наук Орда А.И.

Канд. техн. наук Короленко Г.Т.

 

ã Казаченко Г.В., Кислов Н.В., 2004

В в в е д е н и е

 

Наиболее важными качественными характеристиками мобильных горных машин являются тягово-сцепные свойства и маневренность, которые определяются нагрузками, передаваемыми опорно-ходовыми устройствами на грунт, его физико-механическими свойствами, а также размерами коридора движения. Тягово-сцепные качества зависят от давления на грунт, его распределения по опорной поверхности и деформации последней. Кинематические и геометрические характеристики движения машин в первую очередь определяются скоростью, размерами горных машин и радиусами совершаемых ими поворотов. Давление на опорную поверхность и обусловленные им деформации грунта влияют на мощность, затрачиваемую на передвижение машины. В случае совершения поворотов мощность на передвижение зависит также и от радиуса поворота агрегата.

С практической стороны эти вопросы осваиваются студентами специальности 1-36 10 01 «Горные машины и оборудование» на практических занятиях, посвященных соответственно статическому и тяговому расчетам гусеничных горных машин.

В настоящем пособии изложены теоретические основы и методики выполнения указанных расчетов. Для лучшего усвоения материала в пособии приведены примеры статического и тягового расчетов. Часть расчетов реализуется в виде программ для ПЭВМ.

 

ТЕМА 1. «СТАТИЧЕСКИЙ РАСЧЕТ ГОРНОЙ

ГУСЕНИЧНОЙ МАШИНЫ»

1.1. Обоснование расчетных зависимостей

Задачей статического расчета является нахождение координат центра масс и центра давления, среднего и экстремальных значений давления машины на несущее основание и деформаций последнего, а также определение размеров «ядра сечения» опорной площади гусеничного хода. При проведении расчетов машина рассматривается как механическая система, состоящая из твердых тел. В качестве исходных данных при выполнении задания принимаются размеры гусеничного хода, массы и координаты центров масс составных частей машины и внешние нагрузки, действующие на нее.

Положение центра масс и центра давления определяют степень неравномерности распределения давления под гусеничным ходом и совместно со значениями среднего давления и деформации несущего основания позволяют на начальном этапе проектирования машин оценить рациональность ее компоновки.

Начало системы осей, в которой определяются координаты центра масс и центра давления, удобнее всего связать с машиной и расположить в центре ее опорной поверхности. В этом случае качество компоновки машины, т.е. рациональность пространственного расположения ее составных частей, оценивается мерой близости центра давления к началу системы координат.

Из механики известно, что координаты центра масс механической системы вычисляются по формулам:

, (1.1)

где - масса составной части машины;

- координаты ее центра масс.

При выполнении задания координаты задаются, а при проектировании машины они определяются по ее эскизному чертежу. Для удобства вычислений по формулам (1.1) рекомендуется составить таблицу 1.1.

Таблица 1.1

Данные для вычисления координат центра масс

№ п/п	Наименование составной части машины	Обозначение	Масса, кг	Координаты центра масс, м
	Гусеничный ход				0,2	0,5
...	...	...	...	...	...	...

 

Центром давления машины на грунт называется точка, радиус-вектор которой определяется выражением

, (1.2)

где 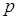- давление машины на грунт в точке с радиус-вектором ;

- площадь опорной поверхности машины;

- элемент этой площади.

Иначе, центр давления представляет собой точку приложения равнодействующей сил давления машины на несущее основание. Из последнего определения следует, что эта точка лежит в опорной плоскости гусеничного хода.

Записав (1.2) в проекциях на оси системы координат, получим:

. (1.3)

Интегралы в числителе выражений (1.3) представляют собой (рис. 1.1) суммарные моменты сил давления машины на грунт относительно осей и , т.е.

.

 

 

Рис. 1.1. К определению моментов и

 

На основании теоремы Вариньона о равенстве момента равнодействующей сумме моментов составляющих можно записать

,

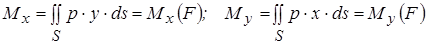где - равнодействующая внешних сил, действующих на машину

(исключая силы реакций грунта на ходовое устройство).

Для горных машин равнодействующая внешних сил представляет геометрическую сумму силы тяжести, приложенной в центре масс, сил реакций разрабатываемой породы на рабочие органы, крюкового усилия и т.п.

Тогда на основании той же теоремы Вариньона (в нашем случае рис. 1.2)

(1.4)

где - сила тяжести;

- равнодействующая внешних сил.

Интеграл, стоящий в знаменателе выражений (1.3), есть общая сила давления машины на несущее основание

,

где - проекция равнодействующей на ось , которая направлена нормально к опорной поверхности,

, (1.5)

где и - соответственно проекции силы тяжести и

равнодействующей внешних сил на ту же ось.

С учетом этого, окончательно

, (1.6)

где и определяются выражениями (1.4), а - выражением (1.5).

Рис 1.2. К определению центра давления

Направление действия силы зависит от способа соединения рабочего органа с машиной. Если рабочий орган закреплен на машине жестко, то направление силы меняется вместе с изменением положения машины, вызываемым неровностью рельефа поверхности или различной деформацией грунта под гусеницами. В этом случае направление силы зафиксировано в системе осей , связанной с машиной. В ряде машин, предназначенных для рытья осушителей или профилирования поверхности, с целью создания постоянного наклона дна осушителей и требуемого профиля поверхности рабочие органы независимо от положения самой машины сохраняют заданное положение относительно неподвижной (инерциальной) системы осей .

Таким образом, направление силы у этих машин всегда ориентировано относительно осей . Напомним, что направление силы совпадает с осью .

Для вычисления , и по формулам (1.4), (1.5) достаточно разложить силы и на проекции по осям , и . Чтобы это сделать, необходимо знать углы между направлением действия сил и названными осями. В нашем случае часть сил (сила ) легко проектируется на оси системы , а другая часть (сила ) может быть ориентирована как в системе , так и в системе .

Чтобы найти проекции сил в одной системе координат по известным проекциям в другой необходимо знать углы или таблицу направляющих косинусов между осями систем.

Направляющие косинусы определяют посредством углов Эйлера , , (рис. 1.3), которые задают ориентацию подвижного триэдра относительно неподвижного . Перевод триэдра в положение осуществляется тремя последовательными поворотами: на угол вокруг оси 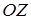, на угол вокруг оси 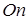, с которой совпадает ось после первого поворота, и на угол вокруг оси , с которой совпадает ось после двух предыдущих поворотов. Заметим, что после первого поворота ось займет положение , ось 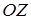после второго поворота совпадает с и после третьего с , ось переходит в промежуточное положение 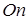после первого поворота и в положение после третьего. Углы , , называются соответственно углами рысканья, поперечного и продольного крена.

 

Рис. 1. 3. Ориентация подвижных осей

 

Таблицу косинусов между подвижными и неподвижными осями вычислим как произведение трех матриц направляющих косинусов, образующихся после каждого из перечисленных поворотов. Обозначив эти матрицы, соответственно через , и , имеем

.

Элементы этой матрицы (рис. 1.3) равны косинусам углов между соответствующими осями (например, ).

Аналогично

;

.

Тогда матрица направляющих косинусов определится как произведение трех приведенных матриц [1]

.

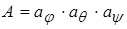Произведя умножение, найдем

(1.7)

 

При статическом расчете машина рассматривается в состоянии покоя, поэтому , , . Приняв для упрощения , приходим к следующему виду таблицы направляющих косинусов:

. (1.8)

Наконец, машина может находиться в положении, когда имеет место только продольный крен, т.е. угол - поперечного крена равен нулю. В этом случае матрица направляющих косинусов имеет еще более простой вид

. (1.9)

Зная направление действия сил в одной из систем, можно при помощи (1.8) и (1.9) найти проекции сил на оси другой системы.

Среднее давление машин на грунт

, (1.10)

где и 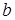- соответственно длина и ширина опорной площади гусеницы.

Если центр давления не совпадает с центром опорной поверхности, то давление машины на грунт распределено неравномерно. Это может привести к тому, что даже при допустимом значении среднего давления машина потеряет проходимость из-за больших деформаций грунта в местах с большими местными давлениями. Поэтому кроме среднего давления вычисляются его наибольшее и наименьшее значения. При этом считают, что деформации несущего основания пропорциональны давлениям, т.е. напряженное состояние грунта подчиняется закону Гука. В этом случае при вычислении максимального и минимального давлений можно воспользоваться формулами сопротивления материалов, определяющими и при внецентренном сжатии-растяжении:

(1.11)

где и - моменты силы 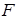относительно соответствующих осей;

и - моменты сопротивления опорной площади относительно

тех же осей.

 

Моменты сопротивления и опорной площади зависят от ее размеров, способа соединения гусениц с рамой машины и количества рядов опорных катков. Для двухопорных гусениц, жестко соединенных с рамой машин

(1.12)

 

где , - моменты инерции опорной площади гусеничного хода

относительно соответствующих осей;

, - наибольшие значения координат

опорной площади;

- поперечная база (колея) машины.

 

Соотношения (1.12) следуют из того, что для двухопорного гусеничного хода при жестком соединении гусениц с рамой машины, его опорная площадь представляет единое сечение сложной формы. Для других конструкций гусеничного хода и должны вычисляться с учетом конструкций гусениц и способа их соединения между собой [2].

Формулы (1.11) показывают, что при достаточно больших значениях и минимальное давление может быть отрицательным. Физически это значит, что часть опорной поверхности гусеничных лент не передает давления на залежь (рис. 1.4).

 

 

 

 

Рис. 1.4. Взаимодействие гусеницы с грунтом при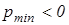

 

Так как опорная площадь гусениц используется не полностью, то среднее давление оказывается большим, чем вычисленное по формуле (1.10). Конструкцию машины, у которой для передачи давления используется не вся опорная поверхность гусеничного хода, что равносильно условию 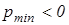, нельзя считать приемлемой. Для того, чтобы выполнялось условие , необходимо, чтобы и были не слишком большими, или, иначе, находились в пределах ядра сечения опорной площади гусениц. Ядром сечения опорной площади называется часть опорной плоскости, при расположении в пределах которой центра давления. Давление во всех точках опорной площади имеет один знак. Применительно к гусеничным машинам это равносильно выполнению условия .

Воспользуемся этим условием для определения формы и размера ядра сечения.

Для двухопорных гусениц, рамы которых жестко связаны между собой, имеем:

или

. (1.13)

Полученное соотношение является уравнением линии, ограничивающей контур ядра сечения, т.е. линии, на которой может располагаться центр давления при условии, что минимальное давление равно нулю. Уравнение (1.13) линейно относительно и . Поэтому контур ядра сечения ограничен прямыми линиями. В уравнение входят модули и , что указывает на симметричность ядра сечения относительно начала координат. Определим наиболее удаленные от начала системы координат точки ядра сечения. Расположим сначала центр давления на оси в положительном направлении.

Тогда 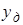= 0 и выражение (1.13) принимает вид:

.

Отсюда максимальное значение в положительном направлении оси

. (1.14)

Аналогично

. (1.15)

Располагая теперь центр давления на оси , т.е. положив 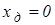, получим

.

Отсюда максимальные удаления центра давления в пределах ядра сечения по оси :

(1.16)

Так как ядро сечения ограничено прямыми, то соединив четыре найденные точки отрезками, убеждаемся, что ядром сечения двухопорного гусеничного хода является ромб (рис. 1.5).

 

 

Рис. 1.5. Ядро сечения

Положение центра давления относительно ядра сечения позволяет судить о рациональности компоновки машины. Если центр давления расположен вне пределов ядра сечения, то взаимное расположение составных частей машины необходимо изменить. При этом нужно стремиться к тому, чтобы центр давления располагался как можно ближе к центру опорной площади.

Среднее и экстремальные значения деформации несущего основания [2]:

(1.17)

где - модуль Юнга несущего основания.

Для обеспечения проходимости необходимо, чтобы 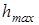не превышало допустимые значения деформации несущего основания.

 

1.2. Порядок выполнения расчета

 

Расчет выполняется на основании исходных данных, которые выдаются на специальном бланке (приложение 1). Последовательность расчетов в целом соответствует порядку изложения теоретического материала в предыдущем разделе. Координаты центра масс определяются по формулам (1.1). Далее вычисляются проекции внешних сил, действующих на машину, на оси подвижной системы координат. При разложении силы тяжести учитывается, что в неподвижной системе она имеет одну проекцию, равную . Пользуясь таблицей направляющих косинусов (1.8) находят проекции силы тяжести на оси :

(1.18)

Для силы , которая ориентирована относительно подвижной системы, имеем:

Таким образом, проекции равнодействующей 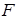внешних сил на оси подвижной системы определяются следующими выражениями:

(1.19)

Выражения (1.19) дают отрицательные значения и , так как (рис. 1.2) эти силы направлены противоположно положительным направлениям осей и .

Моменты и равнодействующей 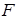относительно осей и проще вычислять с учетом действительного направления сил и . Так как , , то за положительное направление моментов согласно рис. 1.2 целесообразно взять направление по часовой стрелке. С учетом этого находим

(1.20)

где и - координаты точки приложения усилия .

В эти формулы координаты подставляются с учетом их знака, а - со знаком плюс.

После нахождения и последовательно по формулам (1.6), (1.10), (1.11) вычисляются координаты центра давления, среднее и экстремальные значения давления машины на грунт. При этом предварительно определяются моменты сопротивления опорной площади .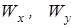

Далее вычисляются размеры ядра сечения (формулы (1.14-1.16)) и строится схема, на которой показывается ядро сечения и положения центра давления. Выполнение задания заканчивается определением средней, наибольшей и наименьшей деформаций грунта по формулам (1.17).

Расчет может быть выполнен на ПЭВМ по программе, имеющейся в ПО кафедры «Горные машины».