Теория систем массового обслуживания
Основные понятия и классификация систем массового
Обслуживания
При решении задач рациональной организации торговли, бытового обслуживания, складского хозяйства и т.д. весьма полезной бывает интерпретация деятельности производственной структуры как системы массового обслуживания (СМО), т.е. системы в которой, с одной стороны, постоянно возникают запросы на выполнение каких-либо работ, а с другой – происходит постоянное удовлетворение этих запросов. Главной особенностью процессов массового обслуживания является случайность.
Всякая СМО включает четыре элемента: входящий поток требований, их очередь на обслуживание, обслуживающее устройство, выходящий поток обслуженных требований.
Требованием (клиентом, заявкой) в СМО называется каждый отдельный запрос на выполнение какой-либо работы. Обслуживание — это выполнение работы по удовлетворению поступившего требования. Объект, выполняющий обслуживание требований, называется обслуживающим устройством (прибором) или каналом обслуживания.
Временем обслуживания называется период, в течение которого удовлетворяется требование на обслуживание, т.е. период от начала обслуживания и до его завершения. Период от момента поступления требования в систему и до начала обслуживания называется временем ожидания обслуживания. Время ожидания обслуживания в совокупности с временем обслуживания составляет время пребывания требования в системе.
СМО классифицируются по разным признакам.
1. По числу каналов обслуживания СМО делятся на одноканальные и многоканальные.
2. В зависимости от условий ожидания требованием начала обслуживания различают СМО с потерями (отказами) и СМО с ожиданием.
В СМО с потерями требования, поступившие в момент, когда все приборы заняты обслуживанием, получают отказ, они теряются для данной системы и никакого влияния на дальнейший процесс обслуживания не оказывают. Классическим примером системы с отказами является телефонная станция – требование на соединение получает отказ, если вызываемый абонент занят. Для системы с отказами основной характеристикой эффективности функционирования является вероятность отказа или средняя доля заявок, оставшихся необслуженными.
В СМО с ожиданием требование, поступившее в момент, когда все приборы заняты обслуживанием, не покидает систему, а становится в очередь и ожидает пока не освободится один из каналов. При освобождении очередного прибора одна из заявок, стоящих в очереди, немедленно принимается на обслуживание.
Для СМО с ожиданием основными характеристиками являются математические ожидания длины очереди и времени ожидания. Примером системы с ожиданием может служить процесс восстановления телевизоров в ремонтной мастерской.
Встречаются системы, лежащие между указанными двумя группами (смешанные СМО). Для них характерно наличие некоторых промежуточных условий: ограничениями могут быть ограничения по времени ожидания начала обслуживания, по длине очереди и т.п.
В качестве характеристик эффективности может применяться вероятность отказа как в системах с потерями (или характеристики времени ожидания) и в системах с ожиданием.
3. По дисциплине обслуживания СМО делятся на системы с приоритетом в обслуживании и на системы без приоритета в обслуживании.
Требования могут обслуживаться в порядке их поступления либо случайным образом, либо в зависимости от установленных приоритетов.
4. СМО могут быть однофазными и многофазными. В однофазных системах требования обслуживаются каналами одного типа (например, рабочими одной профессии) без передачи их от одного канала к другому, в многофазных системах такие передачи возможны.
5. По месту нахождения источника требований СМО делятся на разомкнутые (когда источник требования находится вне системы) и замкнутые (когда источник находится в самой системе).
К замкнутым относятся системы, в которых поступающий поток требований ограничен. Например, мастер, задачей которого является наладка станков в цехе, должен периодически их обслуживать. Каждый налаженный станок становится в будущем потенциальным источником требований на наладку. В подобных системах общее число циркулирующих требований конечно и чаще всего постоянно.
Если питающий источник обладает бесконечным числом требований, то системы называются разомкнутыми. Примерами подобных систем могут служить магазины, кассы вокзалов, портов и т.п. Для этих систем поступающий поток требований можно считать неограниченным.
Методы и модели исследования СМО можно условно разбить на аналитические и статистические (имитационного моделирования процессов массового обслуживания).
Аналитические методы позволяют получить характеристики системы как некоторые функции от параметров ее функционирования. Благодаря этому появляется возможность проводить качественный анализ влияния отдельных факторов на эффективность работы СМО.
К сожалению, аналитическому решению поддается лишь довольно ограниченный круг задач теории массового обслуживания. Несмотря на постоянно ведущуюся разработку аналитических методов, во многих реальных случаях аналитическое решение либо невозможно получить, либо итоговые зависимости оказываются настолько сложными, что их анализ становится самостоятельной трудной задачей. Поэтому ради возможности применения аналитических методов решения приходится прибегать к различным упрощающим предположениям, что в некоторой степени компенсируется возможностью применения качественного анализа итоговых зависимостей (при этом, разумеется, необходимо, чтобы принятые допущения не искажали реальной картины процесса).
Потоки событий. Уравнения Колмогорова
В настоящее время теоретически наиболее разработаны и удобны в практических приложениях методы решения таких задач массового обслуживания, в которых поток требований является простейшим (пуассоновским).
Для простейшего потока частота поступления требований в систему подчиняется закону Пуассона, то есть вероятность поступления за время t, ровно k требований задается формулой:
P k =  e-λt
e-λt
где λ – параметр потока (интенсивность – среднее число требований, поступивших в систему за единицу времени).
Простейший поток обладает тремя основными свойствами: ординарностью, стационарностью и отсутствием последействия.
Ординарность потока означает практическую невозможность одновременного поступления двух и более требований. Например, достаточно малой является вероятность того, что из группы станков, обслуживаемых бригадой ремонтников, одновременно выйдут из строя несколько станков.
Стационарным называется поток, вероятные характеристики которого не зависят от времени. Например, математическое ожидание числа требований, поступающих в систему в единицу времени, является величиной постоянной и называется интенсивностью потока. Таким образом, вероятность поступления в систему определенного количества требований в течение заданного промежутка времени  t зависит от его величины и не зависит от начала его отсчета на оси времени.
t зависит от его величины и не зависит от начала его отсчета на оси времени.
Отсутствие последействия означает, что число требований, поступивших в систему до момента t, не определяет того, сколько требований поступит в систему за время t +  t.
t.
Например, если на ткацком станке в данный момент произошел обрыв нити, и он устранен ткачихой, то это не определяет того, произойдет новый обрыв на данном станке в следующий момент или нет, тем более это не влияет на вероятность возникновения обрыва на других станках.
Вероятность того, что на временном интервале t = τ не поступит ни одного требования p 0 определяется как:
p 0 = e-λτ.
Тогда вероятность того, что на этом же временном интервале появится хотя бы одно требование определяется соотношением
p (t) = 1 – p 0 = 1 – e-λτ.
Вероятность попадания на элементарный временной интервал, т.е. когда τ = Δt, хотя бы одного события (требования) потока, можно определить, заменив функцию e-λτ двумя первыми числами её разложения в ряд Маклорена по степеням Δt. Действительно:
p (Δt) = 1 – e-λΔt ≈ λ Δt.
Важной характеристикой СМО является время обслуживания требований в системе. Время обслуживания является, как правило, случайной величиной и, следовательно, может быть описано законом распределения. Наибольшее распространение в теории и, особенно в практических приложениях, получил экспоненциальный закон. Для этого закона функция распределения вероятностей имеет вид:
р (t <T)=F(t)=1 – е-  t,
t,
т.е. вероятность того, что время обслуживания не превосходит некоторой величины t, где μ – интенсивность потока обслуживания требований в системе (среднее число требований, обслуженных в единицу времени).
Очевидно, что вероятность обслуживания хотя бы одного требования за элементарный временной отрезок будет определяться как:
p (Δt) = 1 – e-Δt ≈ μλ Δt.
При анализе случайных процессов с дискретными состояниями пользуются графиком состояний, где прямоугольником изображаются состояния, а переходы из состояния в состояние – стрелками. У стрелок обычно проставляются значения интенсивностей λij (μij) перехода системы из состояния S i в состояние S j, которые происходят под воздействием простейших потоков событий.
Рассмотрим систему, которая может находиться в двух состояниях: S0– система исправна; S1 – система находится в состоянии отказа и ремонтируется (рис. 8.1).
 |
Рис. 8.1. Граф системы
Будем характеризовать состояние системы (S0,S1) вероятностями состояния р 0 (t) и р 1 (t). Очевидно, что
р 0 (t) + р 1 (t) = 1.
Найдем вероятность того, что система в момент (t+Δt) будет находиться в состоянии S0.
Это возможно, во-первых, в том случае, если система в момент времени t с вероятностью р 0(t) находилась в состоянии S0 и за время Δt из него не вышла. Вероятность выхода системы за время Δt из состояния S0 в состояние S1 определяется как λ· Δt. Противоположная вероятность (что система не выйдет из S0) определяется как (1 – λΔt). Вероятность того, что система, находившаяся в состоянии S0 с вероятностью р 0(t), за время Δt не выйдет из него, равна по теореме умножения вероятностей
р 0(t) (1 – λΔt).
Во-вторых, система в момент времени t находилась с вероятностью р 1(t) в состоянии S1 и за интервал времени Δt с вероятностью μ · Δt перешла в состояние S0, т.е.
р 1(t)· μΔt.
Вероятность р 0(t + Δt) нахождения системы в состоянии S0 момент времени (t + Δt) по какому-либо из двух рассмотренных способов равна сумме рассмотренных вероятностей
р 0(t + Δt) = р 0(t) (1 – λΔt)+ р 1(t) μΔt
Преобразуем соотношение к виду

Переходя к пределу при Δt→ 0, получим

По аналогии составляется уравнение, описывающее вероятность того, что система в момент (t + Δt) будет находиться в состоянии S1, но проще это найти из условия нормирования
р 0 (t) + р 1 (t) = 1.
С учетом этого условия система уравнений для двух состояний графа имеет вид

Задав начальные условия, можно решить систему уравнений и найти систему функций времени рi (t), где i – номер состояния.
Для достаточно большого значения t распределение вероятностей стабилизируется и практически не зависит от времени, т.е.
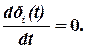
Тогда система уравнений упрощается (стационарный режим)

Откуда вероятности состояний установившегося процесса определяются как


В частности, если μ =2; λ =1, то Р0=0,67; Р1=0,33. Таким образом, в среднем система будет находиться в рабочем состоянии 67%, а в состоянии ремонта 33% времени.
В общем случае система уравнений Колмогорова может быть составлена по следующему алгоритму.
1. В левой части каждого уравнения стоит производная вероятности i -го состояния.
2. В правой части каждого уравнения стоит:
2.1. Сумма произведений вероятностей всех состояний, из которых идут стрелки в i -е состояние, на интенсивности соответствующих потоков событий.
2.2. Минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность i -го состояния.
Система Колмогорова состоит из независимых уравнений и условия нормирования.
СМО с ожиданием
Рассмотрим аналитические модели СМО с ожиданием (наиболее распространенные СМО, в которых требования, поступившие в момент, когда все обслуживающие единицы заняты, становятся в очередь и обслуживаются по мере освобождения обслуживающих единиц).
Задачи с очередями являются типичными в производственных условиях, например при организации наладочных и ремонтных работ, при многостаночном обслуживании и т.д.
Постановка задачи в общем виде выглядит следующим образом.
Система состоит из n обслуживающих каналов. Каждый из них может одновременно обслуживать только одно требование. В систему поступает простейший (пуассоновский) поток требований с параметром  . Если в момент поступления очередного требования в системе на обслуживании уже находится не меньше n требований (т.е. все каналы заняты), то это требование становится в очередь и ждет начала обслуживания. Время обслуживания каждого требования t об является случайной величиной, которая подчиняется экспоненциальному закону распределения с параметром
. Если в момент поступления очередного требования в системе на обслуживании уже находится не меньше n требований (т.е. все каналы заняты), то это требование становится в очередь и ждет начала обслуживания. Время обслуживания каждого требования t об является случайной величиной, которая подчиняется экспоненциальному закону распределения с параметром  .
.
Как отмечалось выше, СМО с ожиданием можно разбить на две большие группы: замкнутые и разомкнутые. Особенности функционирования каждой из этих двух видов систем накладывают свой оттенок на используемый математический аппарат. Расчет характеристик работы СМО различного вида может быть проведен на основе расчета вероятностей состояний СМО (формулы Эрланга).
Замкнутая СМО с ожиданием
Поскольку система замкнутая, то к постановке задачи следует добавить условие: поток поступающих требований ограничен, т.е. в системе обслуживания одновременно не может находиться больше m требований (m – число обслуживаемых объектов).
Такую систему можно классифицировать как многоканальную СМО (n – каналов) и ограниченной данной очереди l, причем n +l = m.
Граф состояний такой системы изображен на рис. 8.2.

Рис. 8.2. Граф состояний многоканальной СМО с ограниченной очередью
Состояния данной системы означают:
S0 – отсутствие требований в системе;
S1 – одно требование обслуживается, очереди нет;
S2 – два требования обслуживаются, очереди нет;
…………………………………………………….
Sn – n требований обслуживаются, очереди нет;
S n+ 1 – n требований обслуживаются, одно требование стоит в очереди;
…………………………………………………….
S n+l – n требований обслуживаются, l требований стоят в очереди.
Система уравнений вероятностей состояний в стационарном режиме для цепочки S0 – Sn будет:

Для цепочки состояний S n+ 1 – S n+l система уравнений стационарного режима будет:

В качестве основных критериев, характеризующих качество функционирования рассматриваемой системы, выберем: 1) отношение средней длины очереди к наибольшему числу требований, находящихся одновременно в обслуживающей системе – коэффициент простоя обслуживаемого объекта; 2) отношение среднего числа незанятых обслуживающих каналов к их общему числу – коэффициент простоя обслуживаемого канала.
Рассмотрим расчет необходимых вероятностных характеристик (показателей качества функционирования) замкнутой СМО.
1. Вероятность того, что в системе находится k требований при условии, когда их число не превышает числа обслуживающих аппаратов п:
P k = αk P0, (1  k
k  n),
n),
где αk =  или αk =
или αk =  ;
;
 ;
;
 – интенсивность поступления требований в систему от одного источника;
– интенсивность поступления требований в систему от одного источника;
 об – средняя продолжительность обслуживания одного требования;
об – средняя продолжительность обслуживания одного требования;
т – наибольшее возможное число требований, находящихся в обслуживающей системе одновременно (m=n+l);
п – число обслуживающих аппаратов;
Р0 – вероятность того, что все обслуживающие аппараты свободны.
2. Вероятность того, что в системе находится k требований при условии, когда их число больше числа обслуживающих аппаратов:
Pk= 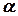 kP0, (n
kP0, (n  k
k  m),
m),
где 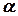 k =
k =  (
(
 об) k или αk =
об) k или αk =  .
.
3. Вероятность того, что все обслуживающие аппараты свободны, определяется из условия

4. Среднее число требований, ожидающих начала обслуживания (средняя длина очереди):
 .
.
5. Коэффициент простоя требования в ожидании обслуживания:
a1= 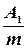 .
.
6. Вероятность того, что все обслуживающие аппараты заняты:
Pотк =  .
.
7. Среднее число требований, находящихся в обслуживающей системе (обслуживаемых и ожидающих обслуживания):
A2= 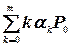 =
=  .
.
8. Коэффициент полного простоя требований на обслуживании и в ожидании обслуживания:
a2=  .
.
9. Среднее время простоя требования в очереди на обслуживание:
Tож= a 1 /  .
.
10. Среднее число свободных обслуживающих аппаратов:
A3=  .
.
11. Коэффициент простоя обслуживающих аппаратов:
a3 = 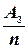 .
.
12. Вероятность того, что число требований, ожидающих обслуживания, больше некоторого числа В (вероятность того, что в очереди на обслуживание находится более В требований):
P-B =  =
= 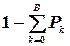 .
.
Рассмотрим пример расчета характеристик замкнутой СМО.
Пример 8.1. Оптовый склад строительных материалов обслуживает шесть предприятий-потребителей материалов. Каждый из потребителей направляет на склад автомашину за материалами в среднем один раз в смену (продолжительность смены 8 ч). На складе имеется один автопогрузчик, который используется только для погрузки материалов на прибывающие автомашины. Прибывшая на склад автомашина становится в очередь, если автопогрузчик занят погрузкой другой автомашины. Обработка статистических данных о продолжительности погрузки одной автомашины и проверка соответствующей гипотезы показали, что продолжительность погрузки одной автомашины подчиняется показательному закону распределения и составляет в среднем 48 мин (0,1 смены). Статистическое исследование потока автомашин показало, что число автомашин, поступающих на склад в единицу времени, подчиняется пуассоновскому закону распределения. Требуется провести расчет характеристик функционирования приведенной производственной системы как СМО.
Решение. Рассчитаем основные параметры системы для условий задачи.
Вероятность того, что все обслуживающие аппараты свободны (на складе нет автомашин) определяется как P0, λ= 1, μ= 0,1.
Вероятность того, что на складе одна автомашина:
P 1 =  0,1 P 0 = 0,6 P 0,
0,1 P 0 = 0,6 P 0,
а вероятность того, что на складе две автомашины (одна под погрузкой, а другая в очереди):
P 2 = 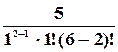 0,12 P 0 = 0,3 P0.
0,12 P 0 = 0,3 P0.
Рассчитывая аналогично, получим: Р 3=0,12 Р 0; Р 4 =0,036 Р 0; Р 5 = 0,0072 Р 0; Р 6 = 0,0007 Р 0. Так как сумма вероятностей нахождения системы в любом из состояний равна 1, т.е.
 =1,
=1,
то P 0(1 + 0,6 + 0,3 + 0,12 + 0,036 + 0,0072 + 0,0007) = 2,0639; Р 0 = 1.
Отсюда находим Р 0 = 0,4845.
Дальнейшие расчеты затруднений не вызывают. Например, средняя длина очереди равна
А 1 =(2 - 1) Р 2 + (3 - 1) Р 3 + (4 - 1) Р 4 + (5 - 1) Р 5 + (6 - 1) Р 6; А = 0,3296.






