Специальные типы полей - 1
Безвихревое векторное поле. Безвихревым векторным полем называют дифференцируемое векторное поле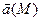 
, заданное в пространственной области 
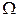, если в любой точке этой области
.
Вообще говоря, следует предположить существование и непрерывность частных производных поля 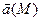- это достаточное условие существования 
, причем условие более сильное, чем дифференцируемость.
Бесциркуляционное векторное поле. Бесциркуляционным называют непрерывное векторное поле 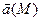, заданное в пространственной области 
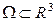, если циркуляция этого поля по любому замкнутому контуру 
, лежащему в 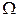, равна нулю, т.е.
(*)
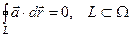В этом случае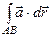 
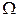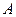не зависит от пути интегрирования, соединяющего в области точки 
и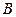 
. (Докажите!). Примером является электростатическое поле, создаваемое заряженными телами конечных размеров.[1]
Работа силового поля
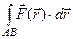- работа силы 
, совершаемая при перемещении материальной точки под действием силы по траектории 
.
Соотношение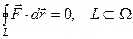 
означает, что работа бесциркуляционного силового поля 
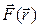вдоль замкнутой траектории равна нулю или, что то же, работа бесциркуляционного силового поля 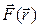не зависит от формы траектории.
Потенциальное векторное поле
Векторное поле 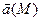, заданное в пространственной области 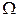, называется потенциальным, если оно является полем градиента некоторого скалярного поля, т.е. существует скалярная функция 
:
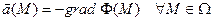. (1)
Скалярное поле называется скалярным потенциалом векторного поля .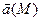
Знак “-“ при определении потенциала соотношением (1) не обязателен и обусловлен удобством физической интерпретации функции . Для силовых полей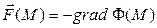 
; возможно определение 
.
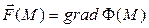- Из соотношения (1) ясно, что потенциал определяется с точностью до аддитивной постоянной.
- Для потенциального поля выражение
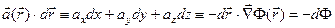(2)
есть полный дифференциал.
- Поверхности уровня скалярного поля называются эквипотенциальными поверхностями.
- Векторные линии потенциального поля
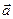ортогональны эквипотенциальным поверхностям. Действительно, 
. Как известно, градиент поля в точке 
ортогонален поверхности уровня в этой точке.
В общем случае безвихревое, бесциркуляционное и потенциальное поле – понятия близкие, но не эквивалентные. Для эквивалентности этих понятий необходимо, чтобы
1) поле 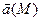было непрерывно дифференцируемым[2];
2) область 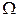определения поля была поверхностно односвязной (т.е. областью, в которой любую простую замкнутую кривую можно путем непрерывной деформации стянуть в точку, не выходя из ).
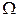Теорема (Ильин, Позняк, стр. 200, Кудрявцев, т. 2, стр.295)
Пусть в поверхностно односвязной области 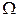задано непрерывно дифференцируемое векторное поле 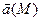. Тогда эквивалентны следующие 3 свойства:
1) Поле 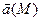является в области 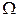потенциальным: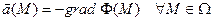
2)
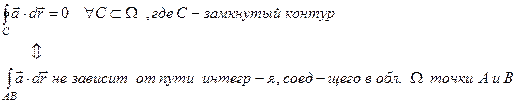
3) Векторное поле 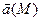является безвихревым: 
.
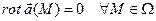Пример. Электростатическое поле в области, где выполнены условия теоремы. Однако потенциальным может быть не только ЭС поле.
Следствия.
1. Пусть 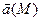- потенциальное поле в поверхностно-односвязной области 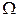. Тогда в силу (2)
,
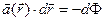где - однозначный потенциал. Следовательно,
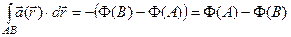. (3)
Итак, непрерывное потенциальное поле в поверхностно-односвязной области является бесциркуляционным.
Если при этом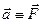 
- силовое поле, то (3) означает, что работа потенциального силового поля в поверхностно-односвязной области не зависит от формы траектории и равна разности значений потенциальной функции в начальной и конечной точках; работа вдоль замкнутой траектории равна нулю.
Нахождение потенциала. Потенциал 
поля 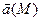можно найти из соотношения (3). Взяв в (3) вместо кривой интегрирования 
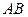произвольную кривую 
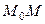, где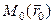 
- некоторая фиксированная, а 
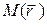произвольная точка области 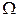, получим:
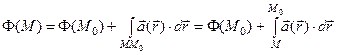(4)
или
, (5)
где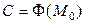 
- произвольная постоянная. (Значение потенциала в произвольной, но фиксированной точке есть произвольная постоянная).
Формулы (4) и (5) дают способ построения однозначного потенциала в поверхностно-односвязной области потенциального поля 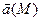. Пусть 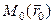- точка, в которой потенциал полагают равным нулю. Тогда
(6)
Потенциал определяется с точностью до аддитивной постоянной. Постоянная определяется выбором точки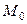 
, в которой потенциал полагают равным нулю.
Итак, если область 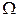определения потенциального поля 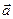поверхностно–односвязна, то 
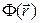- однозначная функция, определяемая по 
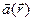с точностью до аддитивной постоянной.
Если область 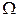многосвязна, то функция 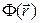может быть многозначной. [3]
Пример. Пусть многосвязная область получается в результате исключения из всего пространства некоторого бесконечного цилиндра. Циркуляция векторного поля по замкнутому контуру, охватывающему цилиндр, может оказаться отличной от нуля. Тогда потенциал (6) многозначен: зависит от того, сколько раз охватывает цилиндр кривая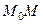 
.
