Сплошное наблюдение предполагает охват всех единиц статистической совокупности.
Если для исследования более целесообразно выборочное наблюдение, то оно должно быть основано на определенных принципах формирования выборочной совокупности.
Выборочным наблюдением называется такое несплошное наблюдение, при котором признаки регистрируются у отдельных единиц совокупности, отобранных с использованием специальных методов, а полученные в процессе обследования результаты с определенным уровнем вероятности распространяются на всю исходную совокупность.
Генеральной совокупностью называется вся исходная изучаемая статистическая совокупность, из которой на основе отбора единиц или групп единиц формируется совокупность выборочная. Генеральная совокупность – это основа выборки.
Отбор единиц в выборочную совокупность может быть повторным и бесповторным.
При повторном отборе попавшая в выборку единица подвергается обследованию, т.е. регистрации значений ее признаков, возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора. При бесповторном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует. Такой отбор возможен, когда размер генеральной совокупности четко определен.
Для определения параметров ошибок выборки применяются следующие обозначения:
N – объем генеральной совокупности;
n – объем выборки;
 – генеральная средняя;
– генеральная средняя;
 – выборочная средняя;
– выборочная средняя;
p – генеральная доля;
w – выборочная доля;
 – генеральная дисперсия;
– генеральная дисперсия;
 – выборочная дисперсия;
– выборочная дисперсия;
 – Среднеквадратическое отклонение;
– Среднеквадратическое отклонение;
 – Среднеквадратическое отклонение выборки;
– Среднеквадратическое отклонение выборки;
Собственно-случайная выборка
Заключается в отборе единиц из генеральной совокупности в целом, без разделения ее на группы. Единицы отбираются в случайном порядке.
| Способ отбора | Предельные ошибки выборки |
| повторный | 
|
| бесповторный | 
|
Механический отбор
Производится по списку единиц генеральной совокупности, расположенному в определенном порядке. Для учета отклонений применяют формулы случайного отбора.
Типический отбор
Вся обследуемая совокупность разбивается на типические группы, из которых в порядке собственно-случайной или механической выборки отбирается нужное число единиц для обследования.
Серийная выборка
Сущность заключается в собственно-случайном или механическом отборе групп единиц, внутри которых проводится сплошное наблюдение.
Тема 10. Изучение взаимосвязи между явлениями
В задачи теории статистики входит исследование объективно существующих взаимосвязей между явлениями. В процессе исследования зависимостей устанавливается причинно-следственная связь между явлениями, и выявляются факторы, оказывающие основное влияние на вариацию изучаемых явлений.
Причинно-следственные отношения – это такая связь явлений, когда изменение одного из них (причины) ведет к изменению другого (следствия).
Социально-экономические явления представляют собой результат одновременного воздействия большого числа причин. Следовательно, при изучении этих явлений необходимо выявить главные причины, абстрагируясь от второстепенных. В статистике существует множество методов изучения взаимосвязи. Их выбор зависит от целей и задач проводимого исследования.
Признаки бывают:
Факторными – обуславливающие изменения связанных с ними признаков;
Результативными – изменяющиеся под воздействием факторных.
Зависимость бывает:
Функциональной – связь, при которой определенному значению факторного признака соответствует только одно значение результативного.
Стохастической – зависимость, проявляющаяся не в каждом отдельном случае, но в среднем при большом числе наблюдений.
По степени тесноты связи:
| Величина коэффициента корреляции | Сила связи |
| До +– 0,3 | Практически отсутствует |
| +– 0,3 – +–0,5 | слабая |
| +– 0,5 – +–0,7 | умеренная |
| +– 0,7 – +–1,0 | сильная |
По направлению связь бывает:
Прямая – при которой с увеличением (уменьшением) значений факторного признака, происходит увеличение (уменьшение) результативного.
Обратная – при которой с увеличением (уменьшением) значений факторного признака, происходит уменьшение (увеличение) результативного.
По аналитическому выражению связь бывает:
Линейной – если связь между явлениями может быть выражена уравнением прямой линии y x = a 0 + a 1 x
Нелинейной – если связь между явлениями выражена уравнением кривой (параболы, гиперболы).
Метод приведения параллельных данных основан на сопоставлении нескольких рядов статистических величин. Такое сопоставление позволяет установить наличие связи и получить представление об ее характере.
Графический метод. Когда речь идет о двухмерных данных, можно нарисовать диаграмму рассеяния, которая позволяет увидеть структуру.
Диаграмма рассеяния представляет каждое наблюдение в пространстве двух измерений, соответствующих двум факторам. Факторный признак обозначается Х, результативный У. Чем сильнее связь между признаками, тем теснее группируются точки вокруг линии, выражающей форму связи.
Корреляция
Обозначается r, является числом от –1 до 1, характеризует силу взаимосвязи данных. R = 1 указывает на идеальную взаимосвязь в виде прямой линии, –1 указывает на идеальную отрицательную взаимосвязь. Обычная интерпретация промежуточных корреляций в промежутке от –1 до 1 заключается в том, что величина (абс. значение) корреляции указывает направление (увеличение или уменьшение).
Линейный коэффициент корреляции характеризует тесноту и направление связи между двумя признаками в случае наличия между ними линейной зависимости.


Множественный коэффициенткорреляции отражает связь между результативным и несколькими факторными признаками.
Частный коэффициент эластичности показывает степень тесноты связи между двумя признаками при фиксированном значении остальных факторных признаков.
Парная регрессия
Парная регрессия позволяет получить аналитическое выражение связи между двумя признаками (результативным и факторным) и может быть представлена в виде прямой, параболы, гиперболы и т. д.
Тип уравнения можно определить, исследуя графическое представление зависимости. Кроме того, если результативный и факторный признаки возрастают одинаково, это свидетельствует о линейной зависимости, при обратной связи – гиперболическая зависимость, если результативный признак увеличивается в арифметической прогрессии, а факторный значительно быстрее, то используется параболическая или степенная зависимость.
Оценка параметров уравнения регрессии осуществляется методом наименьших квадратов. Суть заключается в нахождении параметров а0, а1, при которых минимизируется сумма квадратов отклонений фактических значений результативного признака от теоретических, полученных по выбранному уравнению.
Система уравнений:
 ;
;
 i
i
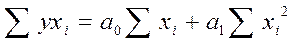
Параметр а0 показывает усредненное влияние на результативный признак неучтенных в уравнении факторных признаков. Коэффициент регрессии а1 показывает, на сколько в среднем изменяется значение результативного признака при увеличении факторного признака на единицу измерения.
Методы изучения связи качественных признаков
При наличии взаимозависимости между вариацией качественных признаков говорят об их ассоциации. Для оценки такой взаимосвязи используют следующие показатели:
1. Коэффициенты ассоциации и контингенции. Они предназначены для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп. Для их вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, т. е. состоящим из двух отличных друг от друга значений признака.
2. Коэффициент взаимной сопряженности Пирсона-Чупрова. Применяется, когда каждый из качественных признаков состоит более чем из двух групп.
Ранговые коэффициенты связи
Ранжирование – процедура упорядочения объектов изучения, которая выполняется на основе предпочтения.
Ранг – это порядковый номер значений признака, расположенных в порядке возрастания или убывания их величин.
Наибольшее значение из непараметрических методов оценки тесноты связи между явлениями имеют ранговые коэффициенты Спирмена и Кендалла. Они могут быть использованы для определения тесноты связи, как между количественными, так и между качественными признаками.
Коэффициент Спирмена (Коэффициент корреляции рангов):
Ρxy = 1 – (6∑di2) / n (n2 – 1), где
di2 – квадрат разности рангов
n – число наблюдений
Коэффициент Кендалла:
τ = 2S / n (n – 1), где
S – сумма разностей между числом последовательностей и числом инверсий по первому признаку.
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение
высшего профессионального образования
«Уральский государственный университет им. А. М. Горького »
Институт управления и предпринимательства
Кафедра экономики, финансов и менеджмента
СТАТИСТИКА
Методические указания
по изучению дисциплины
Составитель: Е. О. Гуман
Екатеринбург






