Мультиколлинеарность - тесная корреляционная взаимосвязь между отбираемыми для анализа факторами, совместно воздействующими на общий результат, которая затрудняет оценивание регрессионных параметров.Существует два основных подхода к решению этой задачи.
§ Метод дополнительных регрессий
§ Строятся уравнения регрессии, которые связывают каждый из регрессоров со всеми остальными
§ Вычисляются коэффициенты детерминации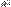 
для каждого уравнения регрессии
§ Проверяется статистическая гипотеза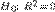 
с помощью F-теста
Вывод: если гипотеза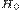 
не отвергается, то данный регрессор не приводит к мультиколлинеарности.
§ Метод последовательного присоединения
§ Строится регрессионная модель с учетом всех предполагаемых регрессоров. По признакам делается вывод о возможном присутствии мультиколлинеарности
§ Расчитывается матрица корреляций и выбирается регрессор, имеющий наибольшую корреляцию с выходной переменной
§ К выбранному регрессору последовательно добавляются каждый из оставшихся регрессоров и вычисляются скорректированные коэффициенты детерминации для каждой из моделей. К модели присоединяется тот регрессор, который обеспечивает наибольшее значение скорректированного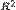 
Процесс присоединения регрессоров прекращается, когда значение скорректированного 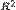становится меньше достигнутого на предыдущем шаге.
Каким бы образом не осуществлялся отбор факторов, уменьшение их числа приводит к улучшению обусловленности матрицы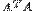 
, а, следовательно, и к повышению качества оценок параметров модели.
Помимо перечисленных методов существует ещё один, более простой, дающий достаточно хорошие результаты — это метод предварительного центрирования. Суть метода сводится к тому, что перед нахождением параметров математической модели проводится центрирование исходных данных: из каждого значения в ряде данных вычитается среднее по ряду: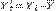 
. Эта процедура позволяет так развести гиперплоскости условий МНК, чтобы углы между ними были перпендикулярны. В результате этого оценки модели становятся устойчивыми
Общие понятия об индексах и значение индексного метода анализа
Способы построения индексов
Разновидности индексов
Агрегатные индексы
Слово «индекс» в переводе с латинского (index) означает «указатель», «показатель». Этот статистический показатель используется для целей сопоставительного анализа развития явления во времени, т.е. является относительной величиной.
Итак, статистический индекс – это относительная величина сравнения сложных совокупностей и отдельных их частей.
Следует иметь в виду, что не всякая относительная величина является индексом. Индексы как сводные статистические показатели исчисляются с учетом специальных принципов и методов, которые в статистике объединяются понятием теории индексного метода.
Прежде всего, индекс – это относительный показатель, получающийся в результате сравнения двух величин, характеризующих уровень изучаемого явления для двух разных периодов.
В теории индексов тот показатель, изменение которого характеризует индекс, называется индексируемой величиной. Величина, которую сравнивают и которая стоит в числителе индексного отношения, характеризует уровень для отчетного периода: чтобы различать отчетный период принято возле символа индексируемой величины внизу ставить знак «1». Величина, с которой сравнивают и которая стоит в знаменателе индексного отношения, характеризует уровень для базисного периода (обозначается внизу символа индексируемого показателя знаком «0»).
Индекс как относительный показатель может быть выражен в виде коэффициентов (когда базовый уровень принят за 1) или в виде процентов (когда он принят за 100). Если индекс больше 1 (или 100%) уровень изучаемого явления растет, если меньше 1 (или 100%) – снижается.
Можно выделить три основные сферы применения индексного метода:
- сравнительная характеристика сложных совокупностей (индексы роста и прироста, индексы выполнения плана, территориальные индексы);
- анализ динамики средних показателей: зависящих от изменения структуры совокупности;
- изучение связей и оценка доли отдельных факторов в изменении сложного явления.
Классификация индексов
1) В зависимости от характера объектов исследования различают индексы объемных и индексы качественных показателей.
К первой группе относятся индексы физического объема продукции, национального дохода, розничного товарооборота, потребления и т.д. Они исчисляются на основе величин объемных показателей.
Ко второй группе относятся индексы себестоимости продукции, производительности труда, цен и т.д. Они исчисляются на основе качественных показателей.
2) По степени охвата элементов (единиц) совокупности индексы делятся на индивидуальные, групповые и общие.
Индивидуальные индексы дают сравнительную характеристику отдельных элементов той или иной совокупности. Например, индекс производства отдельной продукции, цены конкретного товара.
Групповые индексы охватывают часть (какую-то группу) единиц совокупности. Иногда их называют субиндексами. Например, индексы объема производства продукции по отдельным отраслям промышленности.
Общие индексы характеризуют изменение совокупности в целом. По своему содержанию являются сводными относительными показателями. Они выражают среднее изменение, например, объема продукции промышленности, цен, заработной платы.
3) В зависимости от методологии расчета общие и групповые индексы подразделяются на агрегатные (суммарные) и средние из индивидуальных индексов.
Агрегатная форма индексов является основной формой расчета общих индексов. Для расчета агрегатных индексов используются так называемые соизмерители (веса) индекса, которые позволяют преодолеть несоизмеримость отдельных элементов и суммировать разноименные индексируемые величины.
Средний взвешенный из индивидуальных индексов позволяет получить тот же результат, что и агрегатный индекс.
В теории статистики при выборе весов пользуются следующими правилами: индексы динамики количественных (объемных) показателей рассчитывают с весами базового периода, а качественных – с весами текущего периода. Такое правило сообразуется с сущностью рассчитываемых показателей, и, кроме того, позволяет построить систему взаимосвязанных индексов.
4) В зависимости от задач исследования (или выбора периода анализа) могут быть рассмотрены отдельный индекс или ряд индексов.
Отдельный индекс рассчитывается только по двум: отчетному (текущему) и базовому периодам.
Ряд индексов исчисляется за несколько периодов. При этом веса в этом ряду могут быть постоянными, т.е. относящимися у всех индексов к одному периоду, или переменными, т.е. изменяющимися от индекса к индексу. В первом случае говорят о системе (ряде) базисных индексов, а во втором случае получают систему цепных индексов.
Индивидуальные индексы принято обозначать символом «i», а общие индексы - J.
По степени охвата элементов явления индексы делят на индивидуальные и общие (сводные).
Индивидуальные индексы (i) - это индексы, которые характеризуют изменение только одного элемента совокупности.
Общий (сводный) индекс (I) характеризует изменение по всей совокупности элементов сложного явления. Если индексы охватывают только часть явления, то их называют групповыми. Способ построения агрегатных индексов заключается в том, что при помощи так называемых соизмерителей можно выразить итоговые величины сложной совокупности в отчетном и базисном периодах, а затем первую сопоставить со второй.
В статистике имеют большое значение индексы переменного и фиксированного состава, которые используются при анализе динамики средних показателей.
Индексом переменного состава называют отношение двух средних уровней.
Индекс фиксированного состава есть средний из индивидуальных индексов. Он рассчитывается как отношение двух стандартизованных средних, где влияние изменения структурного фактора устранено, поэтому данный индекс называют еще индексом постоянного состава.
В зависимости от характера и содержания индексируемых величин различают индексы количественных (объемных) показателей и индексы качественных показателей.
К индексам количественных (объемных) показателей относятся такие индексы, как индексы физического объема производства продукции, затрат на выпуск продукции, стоимости продукции, а также индексы показателей, размеры которых определяются абсолютными величинами. Используются различные виды индексов количественных показателей.
Индекс физического объема продукции (ФОП) отражает изменение выпуска продукции.
Индивидуальный индекс ФОП отражает изменение выпуска продукции одного вида и определяется по формуле
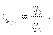где q1 и q0 - количество продукции данного вида в натуральном выражении в текущем и базисном периодах.
Агрегатный индекс ФОП (предложен 
Э. Ласпейресом) отражает изменение выпуска всей совокупности продукции, где индексируемой величиной является количество продукции q, а соизмерителем - цена р:
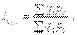где q1 и q0 - количество выработанных единиц отдельных видов продукции соответственно в отчетном и базисном периодах; p0 - цена единицы продукции (отдельного вида) в базисном периоде.
При вычислении индекса ФОП в качестве соизмерителей может выступать также себестоимость продукции или трудоемкость.
Аналогично рассчитывается индекс затрат на выпуск продукции (ЗВП), который отражает изменение затрат на производство и может быть как индивидуальным, так и агрегатным.
Индивидуальный индекс ЗВП отражает изменение затрат на производство одного вида и определяется по формуле
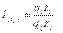где z1 и z0 - себестоимость единицы продукции искомого вида в текущем и базисном периодах; q1 z1 и q0 z0 - суммы затрат на выпуск продукции искомого вида в текущем и базисном периодах.
Агрегатный индекс ЗВП характеризует изменение общей суммы затрат на выпуск продукции за счет изменения количества выработанной продукции и ее себестоимости и определяется по формуле
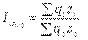где q1 z1 и q0 z0 - затраты на выпуск продукции каждого вида соответственно в отчетном и базисном периодах.
Рассмотрим построение индекса стоимости продукции (СП), который может определяться и как индивидуальный, и как агрегатный.
Индивидуальный индекс СП характеризует изменение стоимости продукции данного вида и имеет вид:
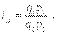где p1 и p0 - цена единицы продукции данного вида в текущем и базисном периодах; q1 p1 и q0 p0 - стоимость продукции данного вида в текущем и базисном периодах.
Агрегатный индекс СП (товарооборота) характеризует изменение общей стоимости продукции за счет изменения количества продукции и цен и определяется по формуле
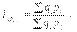Качественные показатели определяют уровень исследуемого итогового показателя и определяются путем соотношения итогового показателя и определенного количественного показателя (например, средняя заработная плата определяется путем соотношения фонда заработной платы и количества работников). К индексам качественных показателей относятся индексы цен, себестоимости, средней заработной платы, производительности труда.
Самым распространенным индексом в этой группе является индекс цен.
Индивидуальный индекс цен характеризует изменение цен по одному виду продукции и определяется по формуле
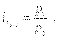где p1 и p0 - цена за единицу продукции в текущем и базисном периодах.
Соответственно определяются индексы себестоимости и затрат рабочего времени по каждому виду продукции.
Агрегатный индекс цен определяет среднее изменение цены р по совокупности определенных видов продукции q.
Для характеристики среднего изменения цен на потребитель-ские товары используют индекс цен, предложенный Э. Ласпейресом (индекс Ласпейреса):
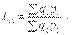где q0 - потребительская корзина (базовый период); p0 и p1 - соответственно цены базисного и отчетного периодов.
Если количество набора продуктов принимается на уровне отчетного периода (q1), то в этом случае индекс цен именуется индексом Пааше:
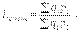(10.11)
В статистической практике очень широко используется агрегатный территориальный индекс цен, который может быть рассчитан по следующей формуле:
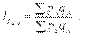где pApB - цена за единицу продукции каждого вида соответственно на территории А и В; qA - количество выработанной или реализованной продукции каждого вида по территории А (в натуральном выражении).
Из формулы видно, что в данном индексе в качестве фиксированного показателя (веса) принят объем продукции территории А. При расчете данного индекса в качестве веса можно принять также объем продукции территории В или суммарный объем продукции двух территорий.
Возможны два способа расчета индексов: цепной и базисный.
Цепные индексы получают путем сопоставления текущих уровней с предшествующим, при этом база сравнения постоянно меняется.
Базисные индексы получают путем сопоставления с тем уровнем периода, который был принят за базу сравнения.
В качестве примера можно привести цепные и базисные индексы цен.
