Статика
Задача С1
Конструкция состоит из жесткого угольника и стержня, которые в точке  или соединены друг с другом шарнирно (рис. С1.0–С1.5), или свободно опираются друг о друга (рис. С1.6–С1.9).
или соединены друг с другом шарнирно (рис. С1.0–С1.5), или свободно опираются друг о друга (рис. С1.6–С1.9).

Рис. С1.0 Рис. С1.1

Рис. С1.2 Рис. С1.3

Рис. С1.4 Рис. С1.5

Рис. С1.6 Рис. С1.7

Рис. С1.8 Рис. С1.9
Внешними связями, наложенными на конструкцию, являются в точке  или шарнир, или жесткая заделка; в точке
или шарнир, или жесткая заделка; в точке  или гладкая плоскость (рис. С1.0 и С1.1), или невесомый стержень
или гладкая плоскость (рис. С1.0 и С1.1), или невесомый стержень  (рис. С1.2 и С1.3), или шарнир (рис. С1.4– С1.9); в точке
(рис. С1.2 и С1.3), или шарнир (рис. С1.4– С1.9); в точке  или невесомый стержень
или невесомый стержень  (рис. С1.0, С1.3, С1.8), или шарнирная опора на катках (рис. С1.7).
(рис. С1.0, С1.3, С1.8), или шарнирная опора на катках (рис. С1.7).
На каждую конструкцию действуют: пара сил с моментом 
 , равномерно распределенная нагрузка интенсивности
, равномерно распределенная нагрузка интенсивности 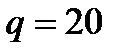
 и еще две силы. Эти силы, их направления и точки приложения указаны в табл. С1; там же в столбце «Нагруженный участок» указано, на каком участке действует распределенная нагрузка (например, в условиях № 1 на конструкцию действуют сила
и еще две силы. Эти силы, их направления и точки приложения указаны в табл. С1; там же в столбце «Нагруженный участок» указано, на каком участке действует распределенная нагрузка (например, в условиях № 1 на конструкцию действуют сила  под углом 60° к горизонтальной оси, приложенная в точке
под углом 60° к горизонтальной оси, приложенная в точке  , сила
, сила  под углом 30° к горизонтальной оси, приложенная в точке
под углом 30° к горизонтальной оси, приложенная в точке  , и нагрузка, распределенная на участке
, и нагрузка, распределенная на участке  ).
).
Определить реакции связей в точках  ,
,  ,
, 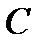 (для рис. С1.0, С1.3, С1.7, С1.8 еще и в точке
(для рис. С1.0, С1.3, С1.7, С1.8 еще и в точке  ), вызванные заданными нагрузками. При окончательных расчетах принять
), вызванные заданными нагрузками. При окончательных расчетах принять  м. Направление распределенной нагрузки на различных по расположению участках указано в табл. С1а.
м. Направление распределенной нагрузки на различных по расположению участках указано в табл. С1а.
Таблица С1
    Сила Сила
| Нагруженный участок | ||||||||
 кН кН
|  кН кН
|  кН кН
| 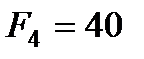 кН кН
| ||||||
| № условия | Точка приложения | α, град | Точка приложения | α, град | Точка приложения | α, град | Точка приложения | α, град | |
| K | – | – | H | – | – | CL | |||
| – | – | L | – | – | E | CK | |||
| L | – | – | K | – | – | AE | |||
| – | – | K | – | – | H | CL | |||
| L | – | – | E | – | – | CK | |||
| – | – | L | – | – | K | AE | |||
| E | – | – | K | – | – | CL | |||
| – | – | H | L | – | – | CK | |||
| – | – | K | – | – | E | CL | |||
| H | – | – | – | – | L | CK |
Таблица С1а
| Участок на угольнике | Участок на стержне | ||
| горизонтальный | вертикальный | рис. С1.0, С1.3, С1.5, С1.7, С1.8 | рис. С1.1, С1.2, С1.4, С1.6, С1.9 |
   
|
Указания. Задача С1 – на равновесие системы тел, находящихся под действием плоской системы сил. При ее решении можно или рассмотреть сначала равновесие всей системы в целом, а затем равновесие одного из тел системы, изобразив его отдельно, или же сразу расчленить систему и рассмотреть равновесие каждого из тел в отдельности, учтя при этом закон о равенстве действия и противодействия. В задачах, где имеется жесткая заделка, учесть, что ее реакция представляется силой, модуль и направление которой неизвестны, и парой сил, момент которой тоже неизвестен.
Пример С1.
На угольник  (
( ), конец
), конец  которого жестко заделан, в точке
которого жестко заделан, в точке  опирается стержень
опирается стержень  (рис. С1,а). Стержень имеет в точке
(рис. С1,а). Стержень имеет в точке  неподвижную шарнирную опору и к нему приложена сила
неподвижную шарнирную опору и к нему приложена сила  , а к угольнику – равномерно распределенная на участке
, а к угольнику – равномерно распределенная на участке  нагрузка интенсивности
нагрузка интенсивности  и пара с моментом
и пара с моментом  .
.
Дано:  кН,
кН, 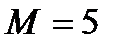
 ,
, 
 ,
,  м.
м.
Определить: реакции в точках  ,
,  ,
,  .
.
Решение:
1. Для определения реакций расчленим систему и рассмотрим сначала равновесие стержня  (рис. С1,б). Проведем координатные оси
(рис. С1,б). Проведем координатные оси  и изобразим действующие на стержень силы: силу
и изобразим действующие на стержень силы: силу 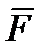 , реакцию
, реакцию  , направленную перпендикулярно стержню, и составляющие
, направленную перпендикулярно стержню, и составляющие  и
и  реакции шарнира
реакции шарнира  . Для полученной плоской системы сил составляем три уравнения равновесия:
. Для полученной плоской системы сил составляем три уравнения равновесия:
 (1)
(1)
 (2)
(2)
 (3)
(3)

Рис. С1
2. Теперь рассмотрим равновесие угольника (рис. С1,в). На него действуют сила давления стержня  , направленная противоположно реакции
, направленная противоположно реакции  , равномерно распределенная нагрузка, которую заменяем силой
, равномерно распределенная нагрузка, которую заменяем силой  , приложенной в середине участка
, приложенной в середине участка  (численно
(численно 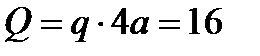 кН), пара сил с моментом
кН), пара сил с моментом 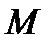 и реакция жесткой заделки, слагающаяся из силы, которую представим составляющими
и реакция жесткой заделки, слагающаяся из силы, которую представим составляющими  и
и  , и пары с моментом
, и пары с моментом  . Для этой плоской системы сил тоже составляем три уравнения равновесия:
. Для этой плоской системы сил тоже составляем три уравнения равновесия:
 (4)
(4)
 (5)
(5)

 . (6)
. (6)
При вычислении момента силы  разлагаем ее на составляющие
разлагаем ее на составляющие  и
и  и применяем теорему Вариньона. Подставив в составленные уравнения числовые значения заданных величин и решив систему уравнений (1)–(6), найдем искомые реакции. При решении учитываем, что
и применяем теорему Вариньона. Подставив в составленные уравнения числовые значения заданных величин и решив систему уравнений (1)–(6), найдем искомые реакции. При решении учитываем, что  в силу равенства действия и противодействия.
в силу равенства действия и противодействия.
Ответ:  кН,
кН,  кН,
кН,  кН,
кН,  кН,
кН,  кН,
кН, 
 . Знаки минус указывают, что силы
. Знаки минус указывают, что силы  ,
,  и момент
и момент  направлены противоположно показанным на рисунках.
направлены противоположно показанным на рисунках.
Кинематика
Задача К1
Под номером К1 помещены две задачи К1а и К1б, которые надо решить.
Задача К1а. Точка  движется в плоскости
движется в плоскости 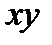 (рис. К1.0–К1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями:
(рис. К1.0–К1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями:  ,
,  , где
, где  и
и  выражены в сантиметрах,
выражены в сантиметрах,  – в секундах.
– в секундах.
Найти уравнение траектории точки; для момента времени  с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
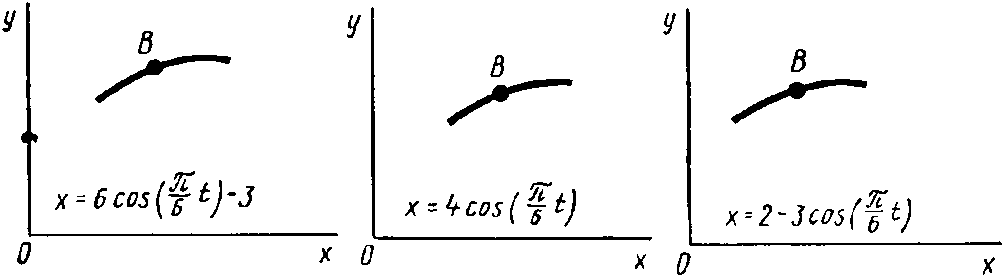
Рис. К1.0 Рис. К1.1 Рис. К1.2

Рис. К1.3 Рис. К1.4 Рис. К1.5

Рис. К1.6 Рис. К1.7 Рис. К1.8

| Рис. К1.9 |
 указана непосредственно на рисунках, а зависимость
указана непосредственно на рисунках, а зависимость  дана в табл. К1 (для рис. К1.0– К1.2 в столбце 2, для рис. К1.3– К1.6 в столбце 3, для рис. К1.7– К1.9 в столбце 4).
дана в табл. К1 (для рис. К1.0– К1.2 в столбце 2, для рис. К1.3– К1.6 в столбце 3, для рис. К1.7– К1.9 в столбце 4).
Задача К1б. Точка движется по дуге окружности радиуса  м по закону
м по закону 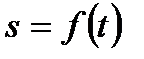 , заданному в табл. К1 в столбце 5 (
, заданному в табл. К1 в столбце 5 ( – в метрах,
– в метрах,  – в секундах), где
– в секундах), где  — расстояние точки от некоторого начала
— расстояние точки от некоторого начала  , измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени
, измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени  с. Изобразить на рисунке векторы
с. Изобразить на рисунке векторы  и
и  , считая, что точка в этот момент находится в положении
, считая, что точка в этот момент находится в положении 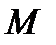 , а положительное направление отсчета
, а положительное направление отсчета  – от
– от  к
к  .
.
Таблица К1
| Номер условия | 
| 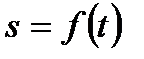
| ||
| Рис. 0–2 | Рис. 3–6 | Рис. 7–9 | ||
12 
| 
| 4 
| 4 
| |
–6 
| 8 
| 6 
| 2 
| |
–3 
| 
| 4 
| 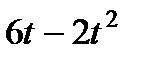
| |
9 
| 
| 10 
| –2 
| |
3 
| 2 
| –4 
| 4 
| |
10 
| 
| 12 
| –3 
| |
6 
| 2 
| –3 
| 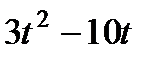
| |
–2 
| 
| –8 
| –2 
| |
9 
| 
| 9 
| 3 
| |
–8 
| 4 
| –6 
| –2 
|
Указания. Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются скорость, касательное и нормальное ускорения точки при естественном способе задания ее движения.
В задаче все искомые величины нужно определить только для момента времени  с. В некоторых вариантах задачи К1а при определении траектории или при последующих расчетах (для их упрощения) следует учесть известные тригонометрические соотношения.
с. В некоторых вариантах задачи К1а при определении траектории или при последующих расчетах (для их упрощения) следует учесть известные тригонометрические соотношения.
Пример К1а.
Даны уравнения движения точки в плоскости 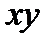 :
:
 ,
, 
( ,
,  – в сантиметрах,
– в сантиметрах,  – в секундах).
– в секундах).
Определить уравнение траектории точки; для момента времени  с найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
с найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Решение:
1. Для определения уравнения траектории точки исключим из заданных уравнений движения время  . Поскольку
. Поскольку  входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу
входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу
 :
:
 . (1)
. (1)
Из уравнений движения находим выражения соответствующих функций и подставляем в равенство (1). Получим
 ,
,  ,
,
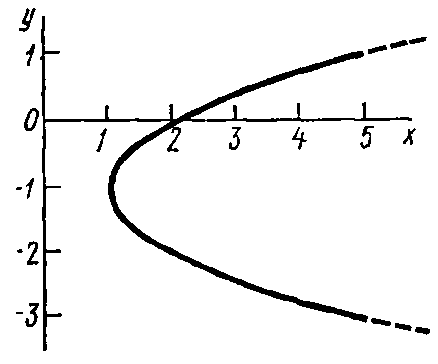 следовательно,
следовательно,
 .
.
Отсюда окончательно находим следующее уравнение траектории точки (параболы, рис. К1,а):
 . (2)
. (2)
| Рис. К1,а |
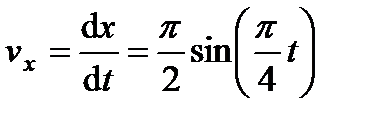 ,
,  ,
,
 .
.
Для момента времени  с:
с: 
 ,
, 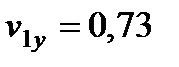
 ,
, 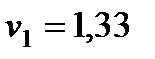
 .
.
3. Аналогично найдем ускорение точки:
 ,
,  ,
,
 .
.
Для момента времени  с:
с: 
 ,
, 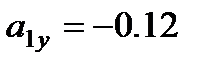
 ,
, 
 . (4)
. (4)
4. Касательное ускорение найдем, дифференцируя по времени равенство:

Получим
 ,
,
откуда
 . (5)
. (5)
Числовые значения всех величин, входящих в правую часть выражения (5), определены и даются равенствами (3) и,(4). Подставив в (5) эти числа, найдем сразу, что при  с:
с: 
 .
.
5. Нормальное ускорение точки  . Подставляя сюда найденные при
. Подставляя сюда найденные при  с числовые значения
с числовые значения  и
и  , получим, что
, получим, что 
 .
.
6. Радиус кривизны траектории  . Подставляя сюда числовые значения
. Подставляя сюда числовые значения  и
и  при
при  с, найдем, что
с, найдем, что  см.
см.
Ответ: 
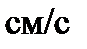 ,
, 
 ,
, 
 ,
, 
 ,
,  см.
см.
Пример К1б.
Точка движется по дуге окружности радиуса  м по закону
м по закону 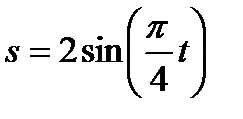 , (
, ( – в метрах,
– в метрах,  – в секундах), где
– в секундах), где  (рис. К1,б).
(рис. К1,б).
Определить скорость и ускорение точки в момент времени  с.
с.
Решение:
Определяем скорость точки:
 .
.
При  с получим
с получим 
 .
.
Ускорение находим по его касательной и нормальной составляющим:

 ,
,
 ,
,
 .
.
| Рис. К1,б |
 с получим
с получим 
 ,
, 
 ,
, 
 .
.
Изобразим на рис. К1,б векторы  и
и  , учитывая знаки и считая положительным направление от
, учитывая знаки и считая положительным направление от 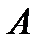 к
к  .
.
Ответ: 
 ,
, 
 .
.
Задача К2
Плоский механизм состоит из стержней 1–4 и ползуна  , соединенных друг с другом и с неподвижными опорами
, соединенных друг с другом и с неподвижными опорами  и
и  шарнирами. Точка
шарнирами. Точка  находится в середине стержня
находится в середине стержня  . Длины стержней равны соответственно
. Длины стержней равны соответственно  м,
м,  м,
м,  м,
м,  м. Положение механизма определяется углами
м. Положение механизма определяется углами  . Значения этих углов и других заданных величин указаны в табл. К2. Точка
. Значения этих углов и других заданных величин указаны в табл. К2. Точка  на всех рисунках и точка
на всех рисунках и точка  на рис. К2.7 – К2.9 в середине соответствующего стержня. Угловое ускорение стержня 1
на рис. К2.7 – К2.9 в середине соответствующего стержня. Угловое ускорение стержня 1  с-1.
с-1.
Дуговые стрелки на рисунках показывают, как при построении чертежа механизма должны откладываться соответствующие углы: по ходу или против хода часовой стрелки (например, угол  на рис. К2.8 отложить от
на рис. К2.8 отложить от  против хода часовой стрелки, а на рис. К2.9 – по ходу часовой стрелки и т.д.).
против хода часовой стрелки, а на рис. К2.9 – по ходу часовой стрелки и т.д.).
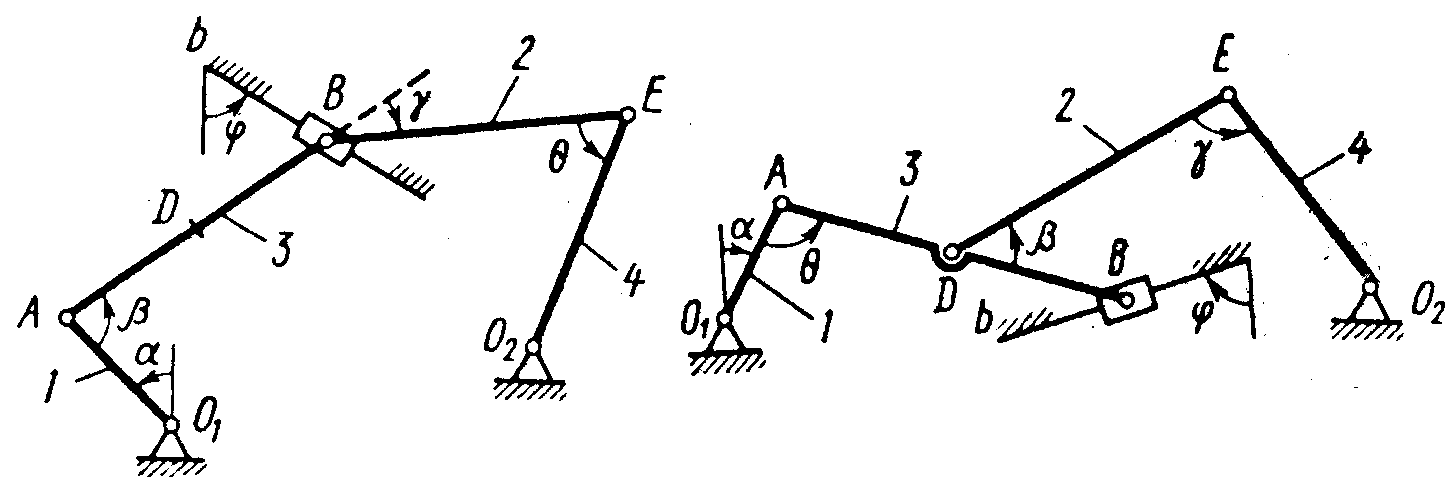
Рис. К2.0 Рис. К2.1

Рис. К2.2 Рис. К2.3

Рис. К2.4 Рис. К2.5

Рис. К2.6 Рис. К2.7

Рис. К2.8 Рис. К2.9
Определить ускорение точки  звена 1 и величины, указанные в таблице в столбце «Найти».
звена 1 и величины, указанные в таблице в столбце «Найти».
Построение чертежа начинать со стержня, направление которого определяется углом  ; ползун с направляющими для большей наглядности изобразить так, как в примере К2 (см. рис. К2б).
; ползун с направляющими для большей наглядности изобразить так, как в примере К2 (см. рис. К2б).
Заданные угловую скорость и угловое ускорение считать направленными против часовой стрелки, а заданную скорость  – от точки
– от точки  к
к  (на рис. К2.5– К2.9).
(на рис. К2.5– К2.9).
Указания. Задача К2 – на исследование плоскопараллельного движения твердого тела. При ее решении для определения скоростей точек механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и понятием о мгновенном центре скоростей, применяя эту теорему (или это понятие) к каждому звену механизма в отдельности.
Таблица К2
| № условия | Углы, град | Дано | Найти | |||||||

| 
| 
| 
| 
| ω1, 1/с | ω4, 1/с | vВ, м/с | ω звена | v точки | |
| – | – | B, E | ||||||||
| – | – | A,D | ||||||||
| – | – | A, E | ||||||||
| – | – | D, E | ||||||||
| – | – | A, B | ||||||||
| – | – | A, E | ||||||||
| – | – | B, E | ||||||||
| – | – | A, D | ||||||||
| – | – | A, E | ||||||||
| – | – | B,E |
Пример К2.
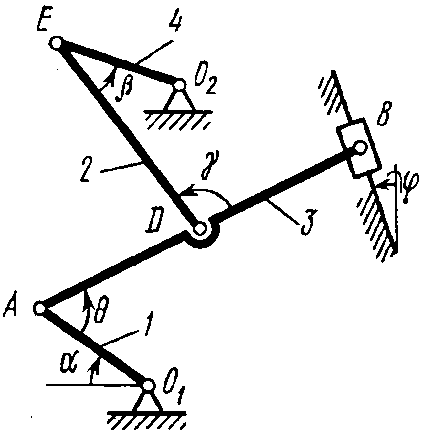 Механизм (рис. К2,а) состоит из стержней 1, 2, 3, 4 и ползуна
Механизм (рис. К2,а) состоит из стержней 1, 2, 3, 4 и ползуна  , соединенных друг с другом и с неподвижными опорами
, соединенных друг с другом и с неподвижными опорами  и
и  шарнирами.
шарнирами.
| Рис. К2,а |
 ,
,  ,
,  ,
, 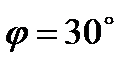 ,
,  ,
,  ,
,  м,
м,  м,
м,  м,
м,  с-1,
с-1,  с-2 (направления
с-2 (направления  и
и  – против хода часовой стрелки).
– против хода часовой стрелки).Определить:  ,
,  ,
,  ,
,  .
.
Решение:
1. Строим положение механизма в соответствии с заданными углами и выбранным масштабом длин (рис. К2,б; на этом рисунке изображаем все векторы скоростей).
 2. Определяем
2. Определяем  . Точка
. Точка  принадлежит стержню
принадлежит стержню  . Чтобы найти
. Чтобы найти  , надо знать скорость какой-нибудь другой точки этого стержня и направление
, надо знать скорость какой-нибудь другой точки этого стержня и направление  . По данным задачи, учитывая направление
. По данным задачи, учитывая направление  , можем определить
, можем определить  . Численно:
. Численно:
 м/с,
м/с,
 . (1)
. (1)
| Рис. К2,б |
 найдем, учтя, что точка
найдем, учтя, что точка  принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная
принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная  и направление
и направление  , воспользуемся теоремой о проекциях скоростей двух точек тела (стержня
, воспользуемся теоремой о проекциях скоростей двух точек тела (стержня  ) на прямую, соединяющую эти точки (прямая
) на прямую, соединяющую эти точки (прямая  ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор
). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор  (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
(проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
 ,
,  м/с. (2)
м/с. (2)
3. Определяем  . Точка
. Точка  принадлежит стержню
принадлежит стержню  . Следовательно, по аналогии с предыдущим, чтобы определить
. Следовательно, по аналогии с предыдущим, чтобы определить  , надо сначала найти скорость точки
, надо сначала найти скорость точки  , принадлежащей одновременно стержню
, принадлежащей одновременно стержню  . Для этого, зная
. Для этого, зная  и
и  , строим мгновенный центр скоростей (МЦС) стержня
, строим мгновенный центр скоростей (МЦС) стержня  . Это точка
. Это точка  , лежащая на пересечении перпендикуляров к
, лежащая на пересечении перпендикуляров к  и
и  , восставленных из точек
, восставленных из точек  и
и  (к
(к  перпендикулярен стержень 1). По направлению вектора
перпендикулярен стержень 1). По направлению вектора  определяем направление поворота стержня
определяем направление поворота стержня  вокруг МЦС
вокруг МЦС  . Вектор
. Вектор  перпендикулярен отрезку
перпендикулярен отрезку  , соединяющему точки
, соединяющему точки  и
и  , и направлен в сторону поворота. Величину
, и направлен в сторону поворота. Величину  найдем из пропорции:
найдем из пропорции:
 . (3)
. (3)
Чтобы вычислить  и
и  , заметим, что
, заметим, что  – прямоугольный, так как острые углы в нем равны 30° и 60°, и что
– прямоугольный, так как острые углы в нем равны 30° и 60°, и что  . Тогда
. Тогда  является равносторонним и
является равносторонним и 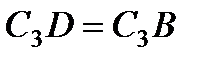 . В результате равенство (3) дает
. В результате равенство (3) дает
 м/с,
м/с,  . (4)
. (4)
Так как точка  принадлежит одновременно стержню
принадлежит одновременно стержню  , вращающемуся вокруг
, вращающемуся вокруг  , то
, то  . Тогда, восставляя из точек
. Тогда, восставляя из точек  и
и  перпендикуляры к скоростям
перпендикуляры к скоростям  и
и  , построим МЦС
, построим МЦС  стержня
стержня  . По направлению вектора
. По направлению вектора  определяем направление поворота стержня
определяем направление поворота стержня  вокруг центра
вокруг центра  . Вектор
. Вектор  направлен в сторону поворота этого стержня. Из рис. К2,б видно, что
направлен в сторону поворота этого стержня. Из рис. К2,б видно, что  , откуда
, откуда  . Составив теперь пропорцию, найдем, что
. Составив теперь пропорцию, найдем, что
 ,
,  м/с. (5)
м/с. (5)
4. Определяем  . Так как МЦС стержня 2 известен (точка
. Так как МЦС стержня 2 известен (точка  ) и
) и 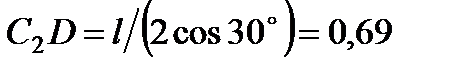 м, то
м, то
 с–1. (6)
с–1. (6)
5. Определяем  (рис. К2,в, на котором изображаем все
(рис. К2,в, на котором изображаем все  векторы ускорений). Точка
векторы ускорений). Точка  принадлежит стержню 1. Полное ускорение точки
принадлежит стержню 1. Полное ускорение точки  разложим на тангенциальную и нормальную составляющие:
разложим на тангенциальную и нормальную составляющие:
 ,
,
где численно
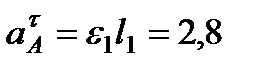 м/с2,
м/с2,
 м/с2. (7)
м/с2. (7)
| Рис. К2,в |
 направлен вдоль
направлен вдоль  , а
, а  – перпендикулярно
– перпендикулярно  . Изображаем эти векторы на чертеже (см. рис. К2в). Вычисляем
. Изображаем эти векторы на чертеже (см. рис. К2в). Вычисляем
 м/с2.
м/с2.
Ответ:  м/с,
м/с, 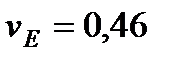 м/с,
м/с,  с–1,
с–1, 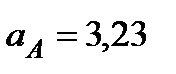 м/с2.
м/с2.
КОНТРОЛЬНЫЕ ВОПРОСЫ
Задача С1
1) Основные виды силовых воздействий и их свойства:
– сосредоточенная сила (проекции силы на оси; момент силы относительно точки как характеристика вращательного действия силы; величина и знак алгебраического момента;
– вращающий момент (пара сил), изображение пары на плоскости, момент пары;
– распределенные силы с постоянной интенсивностью (эпюра распределенных сил, приведение к равнодействующей).
2) Силы активные и реакции связей. Внешние закрепления конструкции (подвижный и неподвижный цилиндрические шарниры, скользящая заделка – втулка, жесткая заделка, невесомый стержень, нить, идеальная поверхность). Как направлены реакции этих связей? Сколько неизвестных составляющих реакции имеет каждая из перечисленных связей? В каком случае реакция связи содержит вращающий момент?
3) Виды представленных в конструкциях соединений тел между собой. Метод разбиения. Внутренние двусторонние и односторонние связи.
4) Каковы аналитические условия равновесия произвольной плоской системы сил?
5) Статическая определимость и неопределимость конструкции. Какие дополнительные условия представлены в задаче, которые делают конструкцию статически определимой? Как определяется статическая определимость в сочлененных конструкциях?
Задача К1
1) Координатный способ задания движения точки.
2) Определение скорости точки. Нахождение скорости при координатном способе задания движения.
3) Определение ускорения. Разложение ускорения на касательную и нормальную составляющие.
4) Естественный способ изучения движения. Определение кинематических характеристик в естественных координатах.
Задача К2
1) Виды движений различных звеньев плоского механизма задачи К2.
2) Поступательное движение.
3) Вращательное движение вокруг неподвижной оси (центра  ). Угловая скорость и угловое ускорение вращающихся звеньев. Как направлены и чему равны скорости точек вращающегося тела?
). Угловая скорость и угловое ускорение вращающихся звеньев. Как направлены и чему равны скорости точек вращающегося тела?
4) Плоскопараллельное движение. Мгновенный центр скоростей и его свойства. Как найдены МЦС звеньев механизма задачи?
5) Как формулируется теорема о проекциях скоростей двух точек тела? Как она используется для нахождения скоростей различных точек механизма?
Библиографический список
1. Никитин Н.Н. Курс теоретической механики: учебник для машиностроит. и приборостроит. спец. вузов / Н.Н. Никитин. – М.: Высш. шк., 1990. 607 с.
2. Бутенин Н.В. Курс теоретической механики: в 2х т. / Н.В. Бутенин, Я.Л. Лунц, Д.Р. Меркин. – СПб.: Лань, 2002. 736 с.
3. Тарг С.М. Краткий курс теоретической механики / С.М. Тарг. – М: Высш. шк., 2008. 416 с.
4. Цывильский В.Л. Теоретическая механика / В.Л. Цывильский. – М: Высш. шк., 2008. 368 с.
5. Переславцева Н.С. Теоретическая механика: учеб. пособие / Н.С. Переславцева, Н.П. Бестужева. – Воронеж: ВГТУ, 2009. – 157 с.
6. Мещерский И.В. Задачи по теоретической механике / И.В. Мещерский. – СПб.: Лань, 2001. 448 с.
7. Сборник заданий для курсовых работ по теоретической механике: учеб. пособие для техн. вузов / под ред. А.А. Яблонского. – М.: Интеграл-Пресс, 2006. 384 с.
содержание
Программа курса....................... 1
Статика........................... 2
Кинематика......................... 3
Кинематика твердого тела................. 4
Содержание контрольных заданий, выбор вариантов,
порядок выполнения работ, общие
пояснения к тексту задач................. 5
Принятые обозначения.................... 7
Задачи к контрольным заданиям.............. 10
Статика. Задача С1.................... 10
Кинематика. Задача К1.................. 16
Задача К2.................. 22
Контрольные вопросы.................... 29
Библиографический список................. 31
Программа, методические указания
и контрольное задание № 1
(статика, кинематика)
по дисциплине
«Теоретическая механика»
для бакалавров всех направлений
заочной и заочной ускоренной форм обучения
Составители:
Переславцева Наталья Сергеевна
Бестужева Наталья Петровна
В авторской редакции
Компьютерный набор Н.С. Переславцевой
Подписано к изданию 30.10.2012.
Уч.-изд. л. 1,9.
ФГБОУ ВПО
«Воронежский государственный технический университет»
394026 Воронеж, Московский просп., 14






