Для характеристики структуры совокупности применяются особые показатели – структурные средние. К таким показателям относятся мода и медиана.
Модой (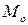 
) называется чаще всего встречающийся вариант.
В дискретном ряду мода – это варианта с наибольшей частотой. В интервальном ряду модой считают центральный вариант модального интервала, т.е. того интервала, который имеет наибольшую частоту (частотность).
Мода для интервального ряда определяется по формуле:
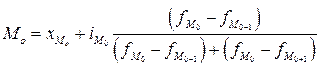, (4.32)
где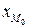 
- нижняя граница модального интервала;
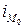- величина модального интервала;
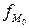- частота, соответствующая модальному интервалу;
- частота, предшествующая модальному интервалу;
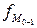- частота интервала, следующего за модальным.
Медиана (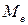 
) – это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значение варьирующего признака меньше, чем средний вариант, а другая – больше.
Для ранжированного ряда (т.е. построенного в порядке возрастания или убывания индивидуальных величин) с нечетным числом членов медианой является варианта, расположенная в центре ряда. Например, данные о стаже работы семи продавцов: 1,2,2,3,5,7,10 – медианой является 4-ая варианта – 3г.
Для ранжированного ряда с четным числом членов медианой будет средняя арифметическая из двух смежных вариант. Например: в бригаде продавцов из 6 человек распределение по стажу работы следующее: 1,3,4,5,7,9 – медиана = (4+5)/2 =4,5г.
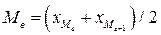. (4.33)
Для интервального вариационного ряда медиана определяется по формуле:
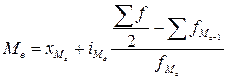, (4.34)
где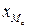 
- нижняя граница медианного интервала;
- величина медианного интервала;
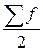- полусумма частот ряда;
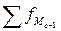- сумма накопленных частот, предшествующих медианному интервалу;
- частота медианного интервала.
Медианный интервал – это интервал, где сумма накопленных частот составляет половину (или больше) всей суммы частот ряда.
Пример: Для приведенного в таблице 4.5 распределения рабочих по размеру заработной платы (гр.1, 2) определить моду и медиану.
Перепишем этот ряд и рассчитаем в нем накопленные частоты:
Таблица 4.5 - Распределение рабочих по размеру заработной платы
| Месячная заработная плата, руб. | Число рабочих,
| Накопленная частота,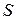 
|
| 8000-8500 | ||
| 8500-9000 | ||
| 9000-9500 | ||
| 9500-10000 | ||
| 10000-10500 | ||
| 10500-11000 | ||
| Итого | - |
Для нахождения моды в данном ряду определяем наибольшую частоту - 60. Этому значению частоты соответствует интервал 9500 - 10000. Следовательно, это и есть модальный интервал. В соответствии с формулой (4.32) мода будет равна:
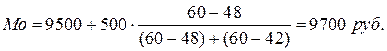
т.е. наиболее часто в данной совокупности рабочих встречается заработная плата в размере 9700 руб.
Для нахождения медианы сначала определяем ее порядковый номер:
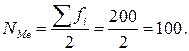
По накопленным частотам видим, что 100-я единица находится также в интервале 9500 - 10000. Ее значение определяется по формуле (4.34):
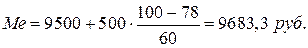
т.е. делаем вывод по медиане, что половина рабочих получает заработную плату ниже 9683,3 руб., а половина - выше.
