Одна звезда.
Уравнение движения планеты.
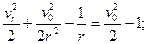
Угловая скорость.
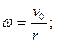
Начальные условия.
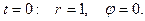
Две звезды
а) неинерциальная система отсчета.
Уравнение движения планеты.
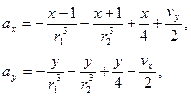
где 
Начальные условия.
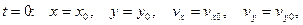
б) инерциальная система отсчета.
Уравнение движения планеты.
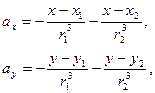
Закон движения звезд.
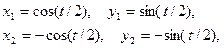
где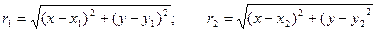 
;
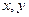- координаты планеты;
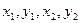- координаты первой и второй звезд.
Начальные условия.
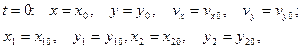
Качественный анализ модели.
В одномерном движении качественный характер движения легко представим, как движение шарика под действием силы тяжести по желобу, профиль которого совпадает с потенциальной кривой. При движении с двумя степенями свободы, потенциальная энергия зависит от двух координат, следовательно, потенциальная кривая превращается в потенциальную поверхность. И в этом случае характер движения системы можно представить как движение шарика под действием силы тяжести по поверхности, рельеф которой совпадает с потенциальной поверхностью.
Так в рассматриваемой задаче потенциальная энергия («настоящая», а не «эффективная»), определяется функцией
.
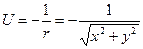Поверхность этой функции показана на рис. 13.9, мысленно опускайте в эту «воронку» маленький шарик, предварительно сообщив ему горизонтальную скорость, и наблюдайте сверху движение шарика как модель движения планеты. Если шарик имеет горизонтальную компоненту скорости, то он никогда не сможет опуститься на большую глубину в эту бесконечно глубокую яму, потому, что с увеличением глубины, радиус ямы уменьшается, поэтому «во имя» сохранения момента импульса скорость шарика должна возрастать до бесконечности, что запрещает закон сохранения энергии.
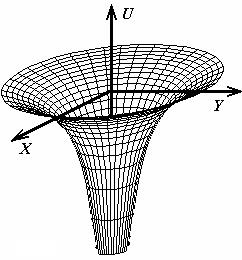
Рис. 13.9
Предельные точки орбиты планеты можно найти, полагая в уравнении закона сохранения энергии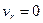 
. Итак, для определения точек возврата имеем уравнение
,
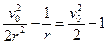корнями которого являются: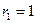 
(это начальное положение) и
.
Кратко повторим возможные виды движений, в зависимости от значения начальной скорости:
а) при 
, то есть планета начинает приближаться к звезде;
б) при 
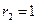, то есть орбита является круговой;
в) при 
, то есть планета начинает удаляться от звезды, но не удаляется на бесконечно большое расстояние;
г) при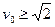 
, кинетической энергии планеты хватает, чтобы преодолеть притяжение звезды, поэтому планета удаляется на бесконечно большое расстояние.
Движение планеты в системе двух звезд тривиально, если расстояние между звездами много меньше расстояний от звезд до планеты, либо расстояние между планетой и одной звездой много меньше расстояния между звездами. Такие задачи сводится к выше рассмотренной – движение планеты около одной звезды. Любые другие варианты порождают очень сложные траектории, трудно поддающиеся качественному анализу. Давайте доверимся модели, раз уж мы ее разрабатываем.
Алгоритм решения.
Одна звезда.
1. Задаем параметры вычислений:
временной шаг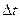 
;
база координат BaseXY.
2. Задаем начальные параметры:
время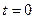 
;
начальный угол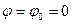 
;
начальную скорость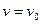 
;
номер узла 
.
3. Определяем текущее время:
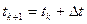
4. Вычисляем ускорение:
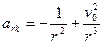
или “если Ньютон не прав”
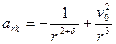
5. Для момента времени 
определяем скорости и координаты:
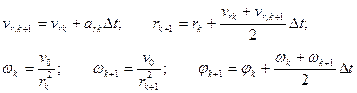
6. Отображаем на экране точки графиков.
7. Переопределяем начальные данные:
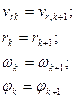
8. Если принудительно не останавливаются вычисления (кнопка ”Стоп”), то переходим к п.3.
9. Завершаем вычисления.
Две звезды.
а) неинерциальная система отсчета.
1. Задаем параметры вычислений:
базовый временной шаг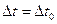 
;
база координат BaseXY.
2. Задаем начальные параметры:
время ;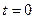
координаты планеты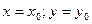 
;
начальную скорость 
;
номер узла .
3. Определяем текущее время:
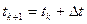
4. Вычисляем ускорение:
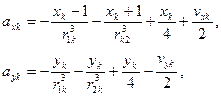
5. Корректируем временной шаг:
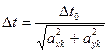
6. Для момента времени определяем скорости и координаты:
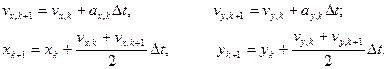
7. Отображаем на экране положение планеты.
8. Переопределяем начальные данные:
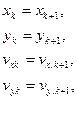
9. Если принудительно не останавливаются вычисления (кнопка ”Стоп”), то переходим к п.3.
10. Завершаем вычисления.
а) инерциальная система отсчета.
1. Задаем параметры вычислений:
базовый временной шаг ;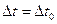
база координат BaseXY.
2. Задаем начальные параметры:
время ;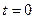
координаты планеты ;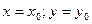
начальную скорость ;
координаты звезд 
;
номер узла .
3. Определяем текущее время:
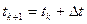
4. Вычисляем ускорение:
5. Корректируем временной шаг:
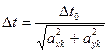
6. Для момента времени определяем скорости и координаты планеты координаты звезд:
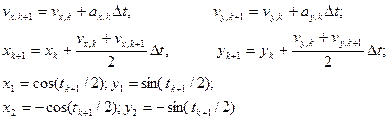
7. Отображаем на экране положение планеты.
8. Переопределяем начальные данные:
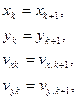
9. Если принудительно не останавливаются вычисления (кнопка ”Стоп”), то переходим к п.3.
10. Завершаем вычисления.
Разработка программы
Интерфейс
Мы уже привыкли для отображения графики использовать компонент Axis (хочется верить, что это не вредная привычка) рис. 3.10. Обратим внимание только на кнопку “Две звезды”. Ee нажатие закрывает текущую форму “Звезда и планета” и открывает вторую форму “Две звезды” рис. 13.11.
Рис. 13.10
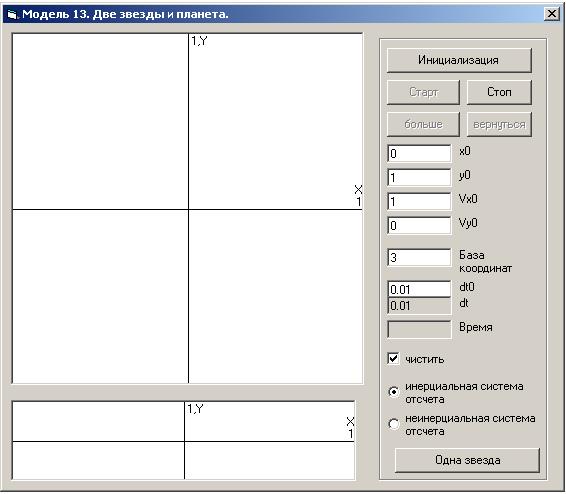
Рис. 13.11
Расстояния между звездами и между звездами и планетой изменяются в больших пределах. Использование одного масштаба при разных начальных условиях не позволяет увидеть детали движения. Частично эту проблему можно решить, задавая разную базу координат. Однако при определенных условиях (например, планета в исходном состоянии находится очень близко к одной из планет) невозможно в обычном масштабе отобразить траекторию планеты. Для изменения масштаба отображения движения планеты предусматриваются две кнопки: "Больше" и "Вернуться". Нажатие первой из них увеличивает масштаб в десять раз и смещает начало координат в текущее положение первой звезды. Если планета находится близко к первой звезде, можно увидеть детали ее траектории. Вторая кнопка возвращает исходный масштаб отображения.
В этой модели (форма 2) мы предусматриваем автоматическое изменение временного шага в зависимости от ускорения планеты (см. формулу (13.32)). В качестве исходного шага вводится базовый шаг времени, а текущий - вычисляемый - просто отображается в текстовом окне.
Программный код.
Форма 1. Звезда и планета.
Option Explicit On
Imports System.Drawing.Color
Imports System.Math
Public Class Form1
'звезда
Dim xStar1 As Single
Dim yStar1 As Single
Dim StarSize As Single = 0.07
'начальные условия
Dim Fi0 As Single 'начальная фаза
Dim v0 As Single
Dim r0 As Single
'планета
Dim xPlanet As Single
Dim yPlanet As Single
Dim xPlanet1 As Single
Dim yPlanet1 As Single
Dim rkPlanet As Single
Dim rk1Planet As Single
Dim akPlanet As Single
Dim ak1Planet As Single
Dim vkPlanet As Single
Dim vk1Planet As Single
Dim omegakPlanet As Single
Dim omegak1Planet As Single
Dim FikPlanet As Single
Dim Fik1Planet As Single
Dim PlanetSize As Single = 0.03
'энергия
Dim En As Single
Dim E0 As Single
Dim Uef As Single
'другие параметры
Dim t As Single 'время
Dim dt As Single 'временной шаг
Dim BaseXY As Single
Dim Delta As Single
В процедуре загрузки формы для обеспечения обинакового масштаба по осям x и y делаем равными высоту и ширину элемента управления Axis1.
Private Sub Form_Load()
Axis1.Width = Axis1.Height
End Sub
Процедура обработки события нажатия кнопки“Инициализация” присваивает переменным, значения параметров, введенные в текстовые поля. Предварительно заблокированниые кнопки“Старт”и “Период” становятся доступными. Эти действия необходимы, чтобы вычисления можно было выполнять только после инициализации параметров.
'инициализация данных
Private Sub CommandInit_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles CommandInit.Click
v0 = Val(Textv0.Text)
dt = Val(TextDT.Text)
BaseXY = Val(TextBaseXY.Text)
Delta = Val(TextDelta.Text)
r0 = 1
Fi0 = 0
rkPlanet = r0
rk1Planet = r0
vkPlanet = 0
vk1Planet = 0
FikPlanet = Fi0
Fik1Planet = Fi0
t = 0
E0 = v0 ^ 2 / 2 - 1
xPlanet = r0
yPlanet = 0
xStar1 = 0
yStar1 = 0
InitAxis()
PlanetSize = 0.05 * BaseXY
StarSize = 0.08 * BaseXY
Axis1.Pix_Size = StarSize
Axis1.PixDraw(xStar1, yStar1, Red, 1)
Axis1.StatToDin()
Axis1.Pix_Size = PlanetSize
Axis1.PixDraw(xPlanet, yPlanet, Blue, 2)
Axis1.DinToPic()
CommandStart.Enabled = True
CommandUef.Enabled = True
End Sub
Private Sub InitAxis()
If Check3.Checked = False Then Exit Sub
'планета
Axis1.Axis_Type = 1
Axis1.Pix_type = 1
Axis1.x_Base = BaseXY
Axis1.y_Base = BaseXY
Axis1.x_Name = "x"
Axis1.y_Name = "y"
Axis1.AxisDraw()
'потенциальная энергия
Axis2.Axis_Type = 2
Axis2.Pix_type = 1
Axis2.Pix_Size = 0
Axis2.x_Base = 4
Axis2.y_Base = 3
Axis2.y_Name = "Uef"
Axis2.x_Name = "r"
Axis2.AxisDraw()
'погрешность вычисления энергии
Axis3.Axis_Type = 2
Axis3.Pix_type = 1
Axis3.Pix_Size = 0
Axis3.x_Base = 40
Axis3.y_Base = 0.001
Axis3.y_Name = "погрешность E"
Axis3.x_Name = "время"
Axis3.AxisDraw()
End Sub
Private Sub CommandStart_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles CommandStart.Click
Timer1.Enabled = True
End Sub
Private Sub Button5_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button5.Click
Timer1.Enabled = False
End Sub
Private Sub Timer1_Tick(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Timer1.Tick
t = t + dt
If Check1.Checked = False Then
akPlanet = (v0 ^ 2 / rkPlanet ^ 3) - (1 / rkPlanet ^ 2)
Else
akPlanet = (v0 ^ 2 / rkPlanet ^ 3) - (1 / rkPlanet ^ (2 + Delta))
End If
vk1Planet = vkPlanet + akPlanet * dt
rk1Planet = rkPlanet + (vkPlanet + vk1Planet) * dt / 2
omegakPlanet = v0 / rkPlanet ^ 2
omegak1Planet = v0 / rk1Planet ^ 2
Fik1Planet = FikPlanet + (omegakPlanet + omegak1Planet) * dt / 2
xPlanet = rkPlanet * Cos(FikPlanet)
yPlanet = rkPlanet * Sin(FikPlanet)
xPlanet1 = rk1Planet * Cos(Fik1Planet)
yPlanet1 = rk1Planet * Sin(Fik1Planet)
'траектория
Axis1.Pix_Size = 0
Axis1.Pix_color = Black
Axis1.Line(xPlanet, yPlanet, xPlanet1, yPlanet1, 1)
'рисуем планету
Axis1.StatToDin()
Axis1.Pix_Size = PlanetSize
Axis1.PixDraw(xPlanet1, yPlanet1, Blue, 2)
Axis1.DinToPic()
'полная энергия
If Check1.Checked = False Then
En = vk1Planet ^ 2 / 2 + (omegak1Planet * rk1Planet) ^ 2 / 2 - 1 / rk1Planet
Uef = v0 ^ 2 / (2 * rk1Planet ^ 2) - (1 / rk1Planet)
Else
'Ньютон не прав
En = vk1Planet ^ 2 / 2 + (omegak1Planet * rk1Planet) ^ 2 / 2 - 1 / ((1 + Delta) * rk1Planet ^ (1 + Delta))
Uef = v0 ^ 2 / (2 * rk1Planet ^ 2) - (1 / ((1 + Delta) * rk1Planet ^ (1 + Delta)))
End If
'эффективная потенциальная энергия
Axis2.PixDraw(rk1Planet, Uef, Blue, 0)
'погрешность
Axis3.PixDraw(t, Abs(E0 - En), Red, 0)
vkPlanet = vk1Planet
rkPlanet = rk1Planet
FikPlanet = Fik1Planet
Textt.Text = Str(Round(t, 2))
End Sub
'эффективная потенциальная энергия
Private Sub CommandUef_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles CommandUef.Click
Dim Uef As Single
Dim Uef1 As Single
Dim r As Single
Dim dr As Single
Dim v0 As Single
Dim dv0 As Single
r = 0.01
dr = 0.01
v0 = 0.5
dv0 = 0.25
Axis1.Pix_color = Red
Do Until v0 > 2
Do Until r > 4 - dr
Uef = v0 ^ 2 / (2 * r ^ 2) - 1 / r
Uef1 = v0 ^ 2 / (2 * (r + dr) ^ 2) - 1 / (r + dr)
Axis2.Line(r, Uef, r + dr, Uef1, 0)
r = r + dr
Loop
v0 = v0 + dv0
r = 0.01
Loop
End Sub
Private Sub TextDT_TextChanged(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles TextDT.TextChanged
If Val(TextDT.Text) > 0.1 Then TextDT.Text = "0.1"
dt = Val(TextDT.Text)
End Sub
Private Sub CommandStar2_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles CommandStar2.Click
Form2.Show()
End Sub
End Class
Форма 2. Звезда и две планеты.
Option Explicit On
Imports System.Drawing.Color
Imports System.Math
Public Class Form2
'звезда
Dim xkStar1 As Double
Dim ykStar1 As Double
Dim xkStar2 As Double
Dim ykStar2 As Double
Dim xk1Star1 As Double
Dim yk1Star1 As Double
Dim xk1Star2 As Double
Dim yk1Star2 As Double
'начальные условия
Dim Fi0 As Double 'начальная фаза
Dim v0 As Double
Dim r0 As Double
'планета
Dim xkPlanet As Double
Dim xk1Planet As Double
Dim ykPlanet As Double
Dim yk1Planet As Double
Dim vxkPlanet As Double
Dim vxk1Planet As Double
Dim vykPlanet As Double
Dim vyk1Planet As Double
Dim xPlanet As Double
Dim yPlanet As Double
Dim xPlanet1 As Double
Dim yPlanet1 As Double
Dim r1Planet As Double
Dim r2Planet As Double
Dim axPlanet As Double
Dim ayPlanet As Double
'энергия
Dim Ek As Double
Dim Ek1 As Double
Dim dE As Double
Dim Uef As Double
Dim A As Double
'другие параметры
Dim t As Double 'время
Dim dt As Double 'временной шаг
Dim dt0 As Double ',базовый временной шаг
Dim BaseXY As Double
Dim Star1Color As Color
Dim Star2Color As Color
Dim RMolPlanet As Double
Dim RMolStar As Double
Dim DispX As Double 'смещение начала координат
Dim DispY As Double 'смещение начала координат
Private Sub CommandStar1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles CommandStar1.Click
Form1.Show()
End Sub
Private Sub Form2_Load(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles MyBase.Load
Star1Color = Red
Star2Color = DarkRed
End Sub
'инициализация данных
Private Sub CommandInit_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles CommandInit.Click
Timer1.Enabled = False
xkPlanet = Val(Textx0.Text)
xk1Planet = Val(Textx0.Text)
ykPlanet = Val(Texty0.Text)
yk1Planet = Val(Texty0.Text)
vxkPlanet = Val(Textvx0.Text)
vxk1Planet = Val(Textvx0.Text)
vykPlanet = Val(Textvy0.Text)
vyk1Planet = Val(Textvy0.Text)
dt0 = Val(TextDT0.Text)
dt = dt0
BaseXY = Val(TextBaseXY.Text)
RMolPlanet = 0.03 * BaseXY
RMolStar = 0.06 * BaseXY
DispX = 0
DispY = 0
t = 0
InitAxis()
xkStar1 = 1
ykStar1 = 0
xkStar2 = -1
ykStar2 = 0
xk1Star1 = 1
yk1Star1 = 0
xk1Star2 = -1
yk1Star2 = 0
Axis1.StatToDin()
Axis1.Pix_Size = RMolPlanet
Axis1.PixDraw(xkPlanet, ykPlanet, Blue, 2)
Axis1.Pix_Size = RMolStar
If RadioButton1.Checked Then
Axis1.PixDraw(xkStar1, ykStar1, Star1Color, 2)
Axis1.PixDraw(xkStar2, ykStar2, Star2Color, 2)
Else
Axis1.PixDraw(xkStar1, ykStar1, Star1Color, 1)
Axis1.PixDraw(xkStar2, ykStar2, Star2Color, 1)
vxkPlanet = vxkPlanet + ykPlanet / 2
vykPlanet = vykPlanet - xkPlanet / 2
vxk1Planet = vxkPlanet
vyk1Planet = vykPlanet
End If
Axis1.DinToPic()
CommandStart.Enabled = True
End Sub
Private Sub InitAxis()
'планета/звезды
Axis1.Axis_Type = 1
Axis1.Pix_type = 1
Axis1.x_Base = BaseXY
Axis1.y_Base = BaseXY
Axis1.x_Name = "x"
Axis1.y_Name = "y"
Axis1.AxisDraw()
'погрешность вычисления энергии
Axis2.Axis_Type = 2
Axis2.Pix_type = 1
Axis2.Pix_Size = 0
Axis2.x_Base = 40
Axis2.y_Base = 0.005
Axis2.y_Name = "погрешность E"
Axis2.x_Name = "время"
Axis2.AxisDraw()
End Sub
Private Sub CommandStart_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles CommandStart.Click
Timer1.Enabled = True
CommandStop.Enabled = True
CommandMore.Enabled = True
CommandBack.Enabled = False
End Sub
Private Sub CommandStop_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles CommandStop.Click
Timer1.Enabled = False
CommandMore.Enabled = False
CommandBack.Enabled = False
End Sub
Private Sub RadioButton1_CheckedChanged(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles RadioButton1.CheckedChanged
Timer1.Enabled = False
CommandStart.Enabled = False
CommandStop.Enabled = False
CommandMore.Enabled = False
CommandBack.Enabled = False
End Sub
Private Sub RadioButton2_CheckedChanged(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles RadioButton2.CheckedChanged
Timer1.Enabled = False
CommandStart.Enabled = False
CommandStop.Enabled = False
CommandMore.Enabled = False
CommandBack.Enabled = False
End Sub
Private Sub Timer1_Tick(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Timer1.Tick
t = t + dt
If RadioButton2.Checked Then
xk1Star1 = 1
xk1Star2 = -1
yk1Star1 = 0
yk1Star2 = 0
'неинерциальная система отсчета
r1Planet = Sqrt((xkPlanet - xk1Star1) ^ 2 + (ykPlanet - yk1Star1) ^ 2)
r2Planet = Sqrt((xkPlanet - xk1Star2) ^ 2 + (ykPlanet - yk1Star2) ^ 2)
axPlanet = -(xkPlanet - xk1Star1) / r1Planet ^ 3 - (xkPlanet - xk1Star2) / r2Planet ^ 3 + xkPlanet / 4 + vykPlanet
ayPlanet = -ykPlanet / r1Planet ^ 3 - ykPlanet / r2Planet ^ 3 + ykPlanet / 4 - vxkPlanet
Else
'инерциальная система отсчета
xk1Star1 = Cos(t / 2)
yk1Star1 = Sin(t / 2)
xk1Star2 = -Cos(t / 2)
yk1Star2 = -Sin(t / 2)
r1Planet = Sqrt((xkPlanet - xk1Star1) ^ 2 + (ykPlanet - yk1Star1) ^ 2)
r2Planet = Sqrt((xkPlanet - xk1Star2) ^ 2 + (ykPlanet - yk1Star2) ^ 2)
axPlanet = -(xkPlanet - xk1Star1) / r1Planet ^ 3 - (xkPlanet - xk1Star2) / r2Planet ^ 3
ayPlanet = -(ykPlanet - yk1Star1) / r1Planet ^ 3 - (ykPlanet - yk1Star2) / r2Planet ^ 3
End If
vxk1Planet = vxkPlanet + axPlanet * dt
vyk1Planet = vykPlanet + ayPlanet * dt
xk1Planet = xkPlanet + (vxkPlanet + vxk1Planet) / 2 * dt + axPlanet * dt * dt / 2
yk1Planet = ykPlanet + (vykPlanet + vyk1Planet) / 2 * dt +ayPlanet * dt * dt / 2
dt = dt0 / Sqrt(axPlanet ^ 2 + ayPlanet ^ 2)
'траектория
Axis1.Pix_color = Black
Axis1.Line(xkPlanet - DispX, ykPlanet - DispY, xk1Planet - DispX, yk1Planet - DispY, 1)
'рисуем планету
Axis1.StatToDin()
Axis1.Pix_Size = RMolPlanet
Axis1.PixDraw(xk1Planet - DispX, yk1Planet - DispY, Blue, 2)
If RadioButton1.Checked Then
'инерциальная система отсчета
Axis1.Pix_Size = RMolStar
Axis1.PixDraw(xk1Star1 - DispX, yk1Star1 - DispY, Star1Color, 2)
Axis1.PixDraw(xk1Star2 - DispX, yk1Star2 - DispY, Star2Color, 2)
xkStar1 = xk1Star1
ykStar1 = yk1Star1
xkStar2 = xk1Star2
ykStar2 = yk1Star2
End If
Axis1.DinToPic()
'изменение энергии
Ek = (vxkPlanet ^ 2 + vykPlanet ^ 2) / 2 - 1 / Sqrt((xkPlanet - xkStar1) ^ 2 + (ykPlanet - ykStar1) ^ 2) - _
1 / Sqrt((xkPlanet - xkStar2) ^ 2 + (ykPlanet - ykStar2) ^ 2)
Ek1 = (vxk1Planet ^ 2 + vyk1Planet ^ 2) / 2 - 1 / Sqrt((xk1Planet - xk1Star1) ^ 2 + (yk1Planet - yk1Star1) ^ 2) - _
1 / Sqrt((xk1Planet - xk1Star2) ^ 2 + (yk1Planet - yk1Star2) ^ 2)
dE = Ek1 - Ek
'работа
A = axPlanet * (xk1Planet - xkPlanet) + ayPlanet * (yk1Planet - ykPlanet)
'погрешность
Axis2.PixDraw(t, Abs(A - dE), Red, 0)
vxkPlanet = vxk1Planet
vykPlanet = vyk1Planet
xkPlanet = xk1Planet
ykPlanet = yk1Planet
Textt.Text = Str(Round(t, 2))
TextDT.Text = Str(Round(dt, 8))
End Sub
Private Sub TextDT_TextChanged(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles TextDT.TextChanged
If Val(TextDT.Text) > 0.1 Then TextDT.Text = "0.1"
dt = Val(TextDT.Text)
End Sub
Private Sub CommandMore_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles CommandMore.Click
CommandBack.Enabled = True
Timer1.Enabled = False
Axis1.Axis_Type = 1
Axis1.Pix_type = 3
Axis1.x_Base = 0.5
Axis1.y_Base = 0.5
Axis1.x_Name = "x"
Axis1.y_Name = "y"
Axis1.AxisDraw()
DispX = xkStar1
DispY = ykStar1
'рисуем планету
Axis1.Pix_Size = RMolPlanet
Axis1.Pix_type = 1
Axis1.PixDraw(xk1Planet - DispX, yk1Planet - DispY, Blue, 2)
'рисуем 1 звезду
Axis1.Pix_Size = RMolStar
Axis1.PixDraw(xk1Star1 - DispX, yk1Star1 - DispY, Star1Color, 2)
Timer1.Enabled = True
End Sub
Private Sub CommandBack_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles CommandBack.Click
CommandMore.Enabled = True
CommandBack.Enabled = False
Timer1.Enabled = False
DispX = 0
DispY = 0
InitAxis()
'рисуем планету
Axis1.StatToDin()
Axis1.Pix_Size = RMolPlanet
Axis1.PixDraw(xk1Planet - DispX, yk1Planet - DispY, Blue, 2)
'рисуем 1 звезду
Axis1.Pix_Size = RMolStar
Axis1.PixDraw(xk1Star1 - DispX, yk1Star1 - DispY, Star1Color, 2)
Axis1.PixDraw(xk1Star2 - DispX, yk1Star2 - DispY, Star2Color, 2)
Axis1.DinToPic()
Timer1.Enabled = True
End Sub
End Class
Тестирование программы.
Тестирование модели “Планета-звезда” выполним на тривиальном примере. Зададим начальную скорость планеты равной 1, тогда орбитой планеты должна быть окружность. Так и получилось! Хотим напомнить (в который раз), что наше тестирование не обеспечивает получение надежных результатов при других исходных параметрах. Это первичный тест, обеспечивающий возможность начала работы с моделью. В качестве подтверждения сказанного выполним несколько экспериментов, обратив внимание на контроль правильности вычислений. На рис. 13.12 для модели "Планета-двойная звезда" приведены шесть «решений» при одних и тех же начальных условиях, полученных для обеих систем уравнений (а-неинерциальная система отсчета) и (б-инерциальная система отсчета) при различных значениях величины 
. Какому из них верить? Да никакому, даже 
оказывается «большим». На всех рисунках совпадают только первая петля вокруг правой звезды и непонятный изгиб траектории в области между звездами, а дальше «траектории» принципиально различаются. Мы специально выбрали такой пример, для которого получить надежное решение не удалось. Причину неудачи при этих начальных условиях выясним чуть позднее.
Рис. 13.12
