Set of 10 test images was used in numerical experiments on kinoforms synthesis with DSRT method. Images have 128×128 pixels and 256 halftones. They are shown in Fig. 2. Small image size was chosen to minimize calculation time.

| 
| 
| 
| 
|

| 
| 
| 
| 
|
Figure 2. Set of 10 test images used in numerical experiments on kinoforms synthesis with DSRT method. Test images are numbered 1-10 from top left to down right
Synthesized kinoforms had 128×128 elements and 16 phase levels. Typical dependency of NSTD of reconstructed image from desired one during iterative process for image number 1 (“Lenna”) is presented in Fig. 3. Iterative algorithm was designed so that it continues to work until NSTD decrease between two last iterations is higher than certain fixed value. For presented dependency this value equals to 0.00005. Initial NSTD value 0.14 corresponds to kinoform generated with Gerchberg-Saxton method (“Gerchberg-Saxton” kinoform). Achieved NSTD value is 0.10. One iteration calculation time is approximately 100 seconds. PC that was used in calculations has AMD FX-8350 eight cores CPU with operating frequency 4.0 GHz and 8 Gb RAM. It should be noted though those 23 iterations were excessive, they merely demonstrate stagnation process. First iteration provides 65% of total NSTD decrease, second iteration – 82%, third – 88%, fourth – 92%, fifth – 94%. Considering each iteration calculation cost, there is not much point to go on after second or third iteration. However, at numerical experiments minimum NSTD decrease between iterations was set to 0.0002 which led to 10÷14 iterations depending on test image.
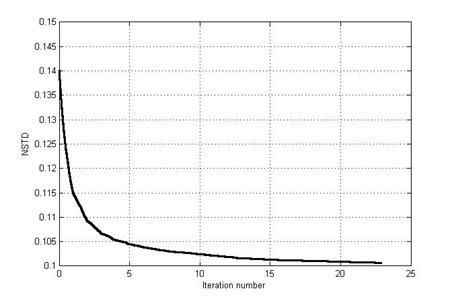
Figure 3. Typical dependency of NSTD of reconstructed image from desired one during iterative process
Images reconstructed from initial “Gerchberg-Saxton” kinoform and from “DSRT” kinoform for test image number 1 are presented in Fig. 4.

| 
|
Figure 4. Images reconstructed from initial “Gerchberg-Saxton” kinoform (left) and from “DSRT” kinoform (right) for test image number 1
It can be seen that image reconstructed from “DSRT” kinoform is significantly less noisy. Results for other test images are similar. They are presented in Table 1. Dependencies of reconstructed images NSTD on test image number for Gerchberg-Saxton and DSRT methods are shown in Fig. 5. Average NSTD of reconstructed images for “Gerchberg-Saxton” and “DSRT” kinoforms equal to 0.152 and 0.115 respectively. NSTD decrease after application of DSRT method varies in range 24÷31%, average NSTD decrease value equals to 26%.
Table 1. NSTD of reconstructed images for Gerchberg-Saxton and DSRT methods
| Test image number | Method | NSTD decrease | |
| Gerchberg-Saxton | DSRT | ||
| 0.140 | 0.101 | 27.9% | |
| 0.157 | 0.120 | 23.6% | |
| 0.152 | 0.115 | 24.3% | |
| 0.150 | 0.114 | 24.0% | |
| 0.134 | 0.093 | 30.6% | |
| 0.144 | 0.106 | 26.4% | |
| 0.143 | 0.104 | 27.3% | |
| 0.149 | 0.110 | 26.2% | |
| 0.152 | 0.115 | 24.3% | |
| 0.153 | 0.115 | 24.8% |

Figure 5. Dependencies of reconstructed images NSTD on test image number for Gerchberg-Saxton and DSRT methods
Conclusion
Method of direct search with random trajectory (DSRT) and its application to task of kinoform synthesis are presented. DSRT method allows for easy change of objective criterion to obtain matrix with desired properties. Calculation costs for arrays with different sizes and quantities of gradations were assessed. DSRT method can work with virtually any initial phase distribution, but it was determined that better and faster results are obtained if in place of initial phase distribution kinoform generated with conventional method is used. We used it in conjunction with well-known Gerchberg-Saxton method. Numerical experiments on synthesis of kinoforms with 128×128 elements and 16 phase levels were performed using set of 10 test images. Results are similar for all used test images. Average normalized standard deviation (NSTD) of reconstructed images for initial “Gerchberg-Saxton” kinoforms and final “DSRT” kinoforms equal to 0.152 and 0.115 respectively. NSTD decrease after application of DSRT method varies in range 24÷31%, average NSTD decrease value equals to 26%.
References
[1] Soifer, V., Kotlyar, V. and Doskolovich, L., [Iterative Methods for Diffractive Optical Elements Computation], Taylor&Francis Ltd., London, 244 p. (1997).
[2] Turunen, J., and Wyrowski, F., [Diffractive Optics for Industrial and Commercial Applications], Akademie Verlag, Berlin, 426 p. (1998).
[3] Soifer, V. A., Doskolovich, L. L. and Kazanskiy, N. L., [Methods for Computer Design of Diffractive Optical Elements], Wiley, USA, 784 p. (2002).
[4] Juptner, W. and Schnars, U., [Digital Holography: Digital Hologram Recording, Numerical Reconstruction, and Related Techniques], Springer-Verlag, Berlin-Heidelberg, 164 p. (2005).
[5] Zwick, S., Haist, T., Warber, M. and Osten, W., “Dynamic holography using pixelated light modulators,” Appl. Opt. 49 (25), F47-F58 (2010).
[6] Evtikhiev, N. N., Starikov, S. N., Cheryomkhin, P. A., Krasnov, V. V., and Rodin, V. G., “Numerical and optical reconstruction of digital off-axis Fresnel holograms,” Proc. SPIE 8429, 84291M (2012).
[7] Doskolovich, L. L., Kazanskiy, N. L., Soifer, V. A., Perlo, P. and Repetto, P. “Design of DOEs for wavelength division and focusing,” Journal of Modern Optics 52 (6), 917-926 (2005).
[8] Bezus, E. A., Doskolovich, L. L., Kazanskiy, N. L., Soifer, V. A. and Kharitonov, S. I. “Design of diffractive lenses for focusing surface plasmons,” Journal of Optics A: Pure and Applied Optics 12 (1), 015001 (2010).
[9] Clemente, P., Duran, V., Torres-Company, V., Tajahuerce, E., and Lancis, J., “Optical encryption based on computational ghost imaging,” Opt. Lett. 35, 2391–2393 (2010).
[10] Evtikhiev, N. N., Starikov, S. N., Cheryomkhin, P. A., Krasnov, V. V., and Rodin, V. G., “Method of optical image coding by time integration,” Proc. SPIE 8429, 84291P (2012).
[11] Lesem, L. B., Hirsch, P. M. and Jordan, J. A. “The Kinoform: A New Wavefront Reconstruction Device,” IBM Journal of Research and Development 13 (2), 150-155 (1969).
[12] Fienup, J. R. “Phase retrieval algorithms: a comparison,” Appl. Opt. 21 (15), 2758-2769 (1982).
[13] Wu, S. T. and Yang, D. K. [Reflective Liquid Crystal Displays], John Wiley and Sons Inc., Chichester, 335 p. (2005).
[14] Evtikhiev, N. N., Krasnov, V. V. and Starikov, S. N., “A method of generating amplitude masks with a constant power spectra and using them to measure the two-dimensional modulation-transfer functions of optical systems,” Journal of Optical Technology 80 (5), 294-300 (2013).
[15] Cheremkhin, P.A., Evtikhiev N.N., Krasnov, V.V., Rodin, V. G.; Starikov S.N., “Generation of keys for image optical encryption in spatially incoherent light aimed at reduction of image decryption error,” Proc. SPIE 9131, 913125 (2014).
[16] Seldowitz, M. A., Allebach, J. P., Sweeney, D. W., “Synthesis of digital holograms by direct binary search,” Appl. Opt. 26, 2788-2798 (1987).
[17] Jennison, B.K., Allebach, J.P., Sweeney, D.W., “Efficient design of direct-binary-search computer-generated holograms,” J. Opt. Soc. Am. 8(4), 652-660 (1991).
[18] Gerchberg, R. W. and Saxton, W. O. “A practical algorithm for the determination of phase from image and diffraction plane pictures,” Optik 75 (2), 237–246 (1972).
[19] Cheremkhin, P. A., Evtikhiev, N. N., Krasnov, V. V., Porshneva, L. A., Rodin, V. G., and Starikov S. N., “Comparison of kinoform synthesis methods for image reconstruction in Fourier plane,” Proc. SPIE 9131, 913124 (2014).
[20] Fienup, J. R. “Invariant error metrics for image reconstruction,” Appl. Opt. 36 (32), 8352-8357 (1997).






