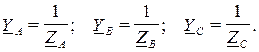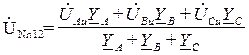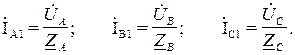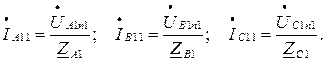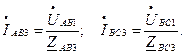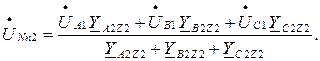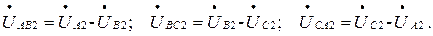Реальная трехфазная электрическая система, как правило, содержит несколько трехфазных приемников, фазы которых соединены по схеме звезда или треугольник, а так же однофазные приемники. Группы приемников соединяются линиями электропередачи между собой и с источником электрической энергии. Такие системы называют разветвленными трехфазными цепями. Поэтому расчет разветвленной трехфазной электрической цепи представляет большое практическое значение.
При расчете сложных трехфазных цепей, имеющих несколько приемников, включенных по различным схемам, а также при расчете цепи с приемником, соединенным треугольником, но с учетом сопротивления линии, приходится использовать преобразование схем, в частности, заменять треугольник эквивалентной звездой и наоборот. Формулы преобразования треугольника в эквивалентную звезду имеют вид:

При симметричной нагрузке имеем:
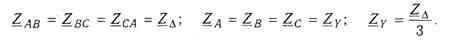
Преобразование звезды в эквивалентный треугольник выполняется по формулам:
При симметричной нагрузке

Если два или несколько приемников соединены звездой, то при симметричной системе линейных напряжений фазные напряжения приемников будут несимметричными, а напряжения между нейтральными точками звезд не будут равными нулю. Следовательно, одноименные фазы приемников нельзя считать соединенными параллельно и проводимости этих фаз складывать нельзя.
Порядок преобразования в этом случае следующий:
1. Звезды преобразовать в эквивалентные треугольники, используя формулы (2).
2. Так как одноименные фазы эквивалентных треугольников присоединены к одинаковым напряжениям, то их можно считать соединенными параллельно и, сложив их проводимости, получить один эквивалентный треугольник.
3. Эквивалентный треугольник преобразовать в эквивалентную звезду, используя формулы (1). В результате схема с несколькими несимметричными звездами преобразована в схему с одной несимметричной звездой (или треугольником), расчет которых разбирался ранее в курсе ТОЭ.
Рассмотрим более сложную трехфазную систему, содержащую два трехфазных приемника, фазы которых включены по различным схемам (рис. 1.1). При этом учтем сопротивления линий электропередачи.
Рис. 1.1
В отличие от рассмотренной ранее симметричной трехфазной цепи заданная схема имеет несимметричную нагрузку:
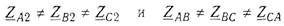
Преобразования и расчет можно выполнить следующим образом.
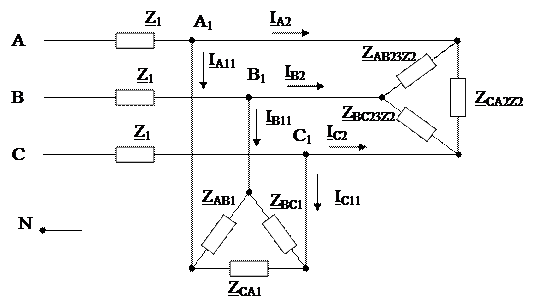
1. Заменить треугольник сопротивлений эквивалентной звездой и сложить сопротивления лучей звезды с сопротивлением линии Z3. Получим две звезды, присоединенные к точкам А1, В1, C1 (рис. 1.1 б).
2. Преобразовать каждую звезду в эквивалентный треугольник и просуммировать проводимости одноименных ветвей. Получим схему с одним эквивалентным треугольником (рис. 1.1 в).
3. Преобразовать эквивалентный треугольник в эквивалентную звезду и сложить сопротивления лучей звезды с сопротивлениями линии Z1
(рис. 1.1 г).
Получена несимметричная звезда без нейтрального провода. Напряжения на фазах этой звезды:
Токи в начале линии:

Если требуется найти токи приемников, то расчет продолжается.
4. Определить фазные и линейные напряжения на зажимах А1, В1, и С1:

5. Определить токи в двух звездах (рис. 1.1 б) аналогично пункту 3. В результате получим токи IА2, IB2 и IC2 исходной звезды и токи IA3, IB3, IC3, равные линейным токам заданного треугольника. Линейные токи треугольника можно определить другим путем, а именно с помощью первого закона Кирхгофа:
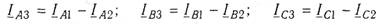
6. Определить фазные и линейные напряжения на зажимах А2, В2, С2
(рис 1.1 а):

7. Определить токи в треугольнике:
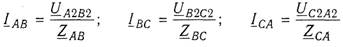
Трехфазная система может одновременно содержать трехфазные и однофазные приемники. В качестве примера рассмотрим трехфазную трехпроводную цепь (рис. 1.2), содержащую симметричный приемник, например, электродвигатель с сопротивлениями фаз Z1 и два однофазных приемника с сопротивлениями Z2 и Z3.
Рис. 1.2
Порядок расчета этой цепи следующий.
1. Выбрать направление токов.
2. Принять за исходную фазу Аи записать в комплексной форме фазные и линейные напряжения:

3. Определить комплексы действующих значений токов трехфазного приемника:

4. Определить токи однофазных приемников:

Задание на курсовую работу
К трехфазному источнику симметричной системы напряжений с линейным напряжением UЛ подключены два несимметричных трехфазных приемника с сопротивлением фаз соответственно ZA1, ZB1, ZC1 и ZAB2, ZBC2, ZCA2 и четыре однофазных приемника ZAB3, ZBС3, ZBС4, ZСА4. По заданным параметрам цепи определить:
1. фазные токи приемников ZA1, ZB1, ZC1, ZAB2, ZBC2, ZCA2, ZAB3, ZBС3, ZBС4, ZСА4;
2. активную, реактивную и полную мощность, а также коэффициент мощности тех же приемников.

Параметры элементов цепи
| UЛ, В
| Z1, Ом
| Z2, Ом
| ZA1, Ом
| ZB1, Ом
| ZC1, Ом
| ZAB2, Ом
| ZBC2, Ом
| ZCA2, Ом
|
|
|
|
|
|
|
|
|
|
|
Линейное напряжение источника: UЛ;
сопротивление провода первой линии электропередачи: Z1;
сопротивление провода второй линии электропередачи: Z2;
сопротивления фаз первого трехфазного приемника: ZA1, ZB1, ZC1;
сопротивления фаз второго трехфазного приемника: ZAB2, ZBC2, ZCA2
сопротивления однофазных приемников ZAB3, ZBС3, ZBС4, ZСА4.
| ZAB3, Ом
| ZBC3, Ом
| ZBC4, Ом
| ZCA4, Ом
|
|
|
|
|
|
Пример расчет цепи
1. Покажем распределение токов в расчетной цепи.


























































Рис. 3.1
2. Объединяем фазы трехфазного и однофазные приемники, подключенные ко второй линии, с учетом того, что они включены параллельно (рис. 3.2):







































Рис. 3.2

3. Преобразуем треугольник второго приемника ZAB2, ZBC24, ZCA24 (рис. 3.2) в эквивалентную звезду ZA2, ZB2, ZC2 (рис. 3.3):
Рис. 3.3
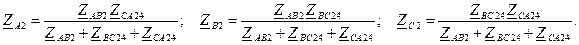
4. Сложим сопротивления лучей второй звезды с сопротивлением линии Z2 с учетом того, что они включены последовательно (рис. 3.4):




































Рис. 3.4
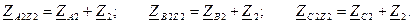
5. Преобразуем звезду первого и второго приемника в эквивалентные треугольники (рис. 3.5):
Рис. 3.5


6. Объединяем второй треугольник с однофазными приемниками, подключенными к первой линии, с учетом того, что они включены параллельно (рис. 3.6):
Рис. 3.6
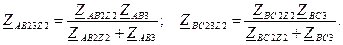
7. Объединяем два треугольника в один эквивалентный треугольник с учетом того, что одноименные фазы включены параллельно (рис. 3.7):
Рис. 3.7

8. Преобразуем треугольник в эквивалентную звезду (рис. 3.8):
Рис. 3.8

9.  Сложим сопротивления лучей звезды с сопротивлениями линии Z1 с учетом того, что они включены последовательно (рис. 3.9):
Сложим сопротивления лучей звезды с сопротивлениями линии Z1 с учетом того, что они включены последовательно (рис. 3.9):
Рис. 3.9

10. Определим проводимости фаз полученной звезды:
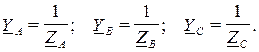
11. Представляем фазные напряжения источника в комплексной форме:

12. Определяем напряжение между нейтралью источника N и нейтралью приемника n12 (рис. 3.9):
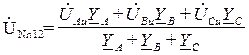
13. Определяем напряжения на фазах звезды.

14. Определяем токи в линии Z1 (рис. 3.9):
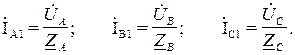
15. Определяем напряжения на точках А1, В1, С1 по отношению к нейтрали источника N (рис. 3.8):

16. Определим проводимости фаз звезды первого приемника (рис. 3.4):

17. Определяем напряжение между нейтралью источника N и нейтралью первого приемника n1 (рис. 3.4):

18. Определяем напряжения на фазах первого приемника (рис. 3.4):

19. Определяем фазные токи первого приемника (рис. 3.4):
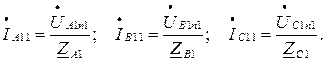
20. Определяем линейные напряжения между точками А1, В1, С1

21. Определяем токи однофазных приемников подключенных к точкам А1, В1, С1 (рис. 3.1):
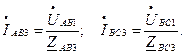
22. Определим проводимости фаз второй звезды (рис. 3.4):

23. Определяем напряжение между нейтралью источника N и нейтралью второй звезды n2 (рис. 3.4):
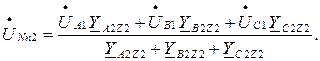
24. Определяем напряжения на фазах второй звезды (рис. 3.4):

25. Определяем токи в линии Z2 (рис. 3.4):

26. Определяем напряжения на точках А2, В2, С2 по отношению к нейтрали источника N (рис. 3.3):

27. Определяем линейные напряжения между точками А2, В2, С2:
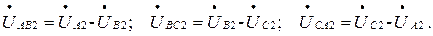
28. Определяем фазные токи в треугольнике второго приемника (рис. 3.1):

29. Определяем токи однофазных приемников, подключенных к точкам А2, В2, С2 (рис. 3.1):

30. Определим мощность и коэффициент мощности первого трехфазного приемника:

31. Определим мощность и коэффициент мощности однофазных приемников подключенных к точкам А1, В1, С1

32. Определим мощность и коэффициент мощности однофазных приемников подключенных к точкам А2, В2, С2

33. Определим мощность и коэффициент мощности второго трехфазного приемника:

Список рекомендуемой литературы
1. Бессонов Л.А. Теоретические основы электротехники. – М.: Высшая школа, 1984.
2. Нейман Л.Р., Демирчан К.С. Теоретические основы электротехники. – Л.: Энергоиздат, 1981.
3. Горбунов А.Н., Кабанов И.Д., Кравцов А.В., Редько И.Я. Теоретические основы электротехники. – М.: УМЦ «Триада», 2005.
4. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
5. Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. М.:Энергия, 1972. –240с.
6. Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.: Энергия- 1972. –200с.


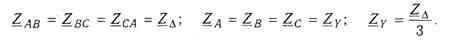



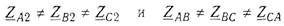



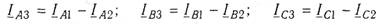

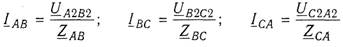




















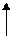










































 Рис. 3.1
Рис. 3.1






































 Рис. 3.2
Рис. 3.2


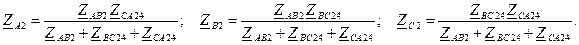



































 Рис. 3.4
Рис. 3.4
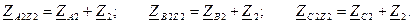
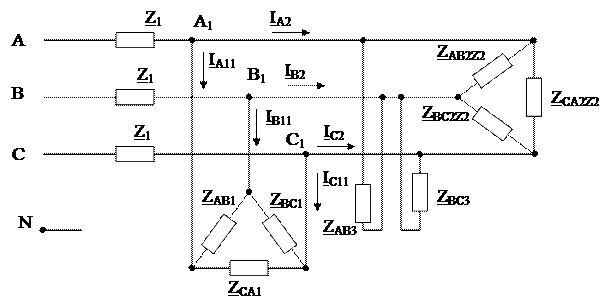


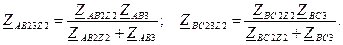



 Сложим сопротивления лучей звезды с сопротивлениями линии Z1 с учетом того, что они включены последовательно (рис. 3.9):
Сложим сопротивления лучей звезды с сопротивлениями линии Z1 с учетом того, что они включены последовательно (рис. 3.9):