Лекция 8. Теоремы сложения и умножения вероятностей. Формула полной вероятности
Содержание
1. Вероятность суммы несовместных событий
2. Зависимые и независимые события
3. Вероятность произведения двух независимых событий
4. Условная вероятность
5. Вероятность произведения зависимых событий
6. Вероятность суммы совместных событий
7. Формула полной вероятности
Вероятность суммы несовместных событий
Теорема. Вероятность суммы несовместных событий равна сумме вероятностей этих событий:  , где
, где 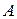 и
и 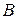 - несовместные события.
- несовместные события.
Замечание. Теорема верна и для  попарно несовместных событий.
попарно несовместных событий.
Следствие. Рассмотрим противоположные события 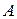 и
и  . Эти события несовместны, причем событие
. Эти события несовместны, причем событие  достоверное. Отсюда
достоверное. Отсюда 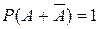 . Но
. Но 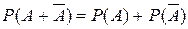 , поэтому
, поэтому 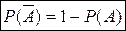 .
.
Пример 1. Компания производит 1000 персональных компьютеров в год, которые реализуются в регионы России и на экспорт. Из них: 150 – в Западную Сибирь, 250 – в Восточную Сибирь. Чему равна вероятность того, что компьютер будет продан в Сибири?
Решение. Введем события:
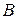 - «Компьютер будет продан в Западную Сибирь»;
- «Компьютер будет продан в Западную Сибирь»; 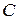 - «Компьютер будет продан в Восточную Сибирь». Эти события несовместны. Их вероятности равны
- «Компьютер будет продан в Восточную Сибирь». Эти события несовместны. Их вероятности равны 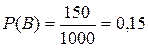 ;
; 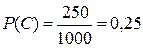 .
.
Событие  означает, что компьютер будет продан в Сибири, т.е. он будет продан или в Западную Сибирь, или в Восточную Сибирь.
означает, что компьютер будет продан в Сибири, т.е. он будет продан или в Западную Сибирь, или в Восточную Сибирь.
Тогда вероятность суммы несовместных событий  равна
равна 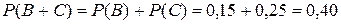 .
.
Зависимые и независимые события
Два события называются зависимыми, если вероятность появления одного из них зависит от появления или непоявления другого события. Два события называются независимыми, если вероятность появления одного из них не зависит от появления другого события
Пример 2. Из урны, в которой находятся 8 белых и 12 черных шаров, последовательно вынимают два шара и обратно не возвращают. Событие 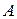 - 1-й вынутый шар черный, событие
- 1-й вынутый шар черный, событие 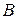 - 2-й вынутый шар черный. Выясним, зависимы ли события
- 2-й вынутый шар черный. Выясним, зависимы ли события 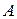 и
и 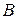 .
.
Пусть произошло событие 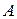 , то есть1-й вынутый шар черный. Тогда в урне осталось 19 шаров, из них 11 черных. Поэтому вероятность события
, то есть1-й вынутый шар черный. Тогда в урне осталось 19 шаров, из них 11 черных. Поэтому вероятность события 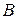 равна
равна 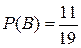 .
.
Пусть теперь не произошло событие 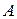 , то есть произошло событие
, то есть произошло событие  , то есть1-й вынутый шар не черный, то есть 1-й вынутый шар белый. Тогда в урне осталось 19 шаров, из них по-прежнему 12 черных. Поэтому вероятность события
, то есть1-й вынутый шар не черный, то есть 1-й вынутый шар белый. Тогда в урне осталось 19 шаров, из них по-прежнему 12 черных. Поэтому вероятность события 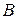 равна
равна 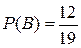 .
.
Мы видим, что вероятность появления события 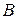 зависит от появления или непоявления события
зависит от появления или непоявления события 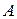 . Значит, события
. Значит, события 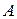 и
и 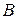 зависимы.
зависимы.
Вероятность произведения двух независимых событий
Теорема. Вероятность произведения независимых событий равна произведению вероятностей этих событий: 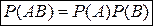 , где
, где 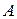 и
и 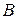 - независимые события.
- независимые события.
Пример 3. Определим вероятность выпадения двух единиц при двух бросаниях кубика.
Событие 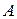 - при 1-м бросании выпало число 1, событие
- при 1-м бросании выпало число 1, событие 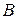 - при 2-м бросании выпало число 1. Тогда событие
- при 2-м бросании выпало число 1. Тогда событие 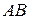 - оба раза выпало число 1.
- оба раза выпало число 1.
События 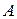 и
и 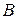 независимы, так как результаты при втором бросании кубика не зависят от того, что выпало при первом бросании.
независимы, так как результаты при втором бросании кубика не зависят от того, что выпало при первом бросании. 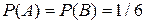 . Тогда
. Тогда  .
.
Условная вероятность
Условной вероятностью  события
события 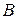 относительно события
относительно события 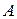 называется вероятность события
называется вероятность события 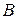 при условии, что событие
при условии, что событие 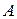 произошло. Тогда для зависимых событий
произошло. Тогда для зависимых событий 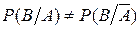 . Для независимых событий
. Для независимых событий  .
.
Пример 4. В примере 2 вероятность  =
=  (2-й вынутый шар черный при условии, что 1-й вынутый шар черный) = 11/19.
(2-й вынутый шар черный при условии, что 1-й вынутый шар черный) = 11/19.  =
=  (2-й вынутый шар черный при условии, что 1-й вынутый шар не черный) = 12/19. Поэтому события
(2-й вынутый шар черный при условии, что 1-й вынутый шар не черный) = 12/19. Поэтому события 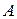 и
и 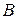 зависимы.
зависимы.






