В любой системе связи через канал передаётся информация. Её скорость определяется по формуле:
I’(А,В)=H’(А)-H’(А|В)=H’(А)-H’(В|А). (1)
Величина H (A | B) - это потери информации при передаче ее по каналу. Ее также называют ненадежностью канала. H (B | A) - энтропияшума; показывает, сколько бит шумовой информации примешивается к сигналу. Передачу сигнала по каналу иллюстрирует рис. 1.

Рис. 1. Передача информации по каналу с помехами
Здесь I ’(A, B)= v * I (A, B) - скорость передачи информации по каналу.
Как видно из формулы (1), эта скорость зависит не только от самого канала, но и от свойств подаваемого на его вход сигнала и поэтому не может характеризовать канал как средство передачи информации.
Рассмотрим дискретный канал, через который передаются в единицу времени u символов из алфавита объёмом m. При передачи каждого символа в среднем по каналу проходит количество информации
I (A,B)=H(A)-H(A|B)=H(B)-H(B|A), (2)
где А и В- случайные символы на входе и выходе канала. Из четырёх фигурирующих здесь энтропий Н(А)- собственная информация передаваемого символа определяется источником дискретного сигнала и не зависит от свойств канала. Остальные три энтропии в общем случае зависят как от источника сигнала, так и от канала.
Величина I (A, B) характеризует не только свойства канала, но и свойства источника информации. Пусть на вход канала можно подавать сигналы от различных источников информации с различными распределениями P (A). Для каждого источника I (A, B) примет свое значение. Максимальноеколичествоинформации, взятое по всевозможным Р (А), характеризует только канал и называется пропускнойспособностью (ПС) канала в расчете на один символ:
 бит/символ,
бит/символ,
где максимизация производится по всем многомерным распределениям вероятностей Р(А).
Также определяют пропускную способность С канала в расчете на единицу времени:
 бит/с, (3)
бит/с, (3)
где v - количество символов, переданное в секунду.
В качестве примера вычислим пропускную способность дискретного симметричного канала без памяти (рис. 2) с вероятностью ошибочного перехода - p.

Рис. 2. Модель двоичного симметричного канала без памяти
Согласно свойству взаимной информации 2 можно записать: С сим=max(H (B)- H (B | A)). Распишем H (B | A). Исходя из условий задачи вероятность правильной передачи символа по каналу - 1-p, а вероятность ошибочной передачи одного символа p /(1- m), где m - число различных символов, передающихся по каналу. Общее количество верных передач - m; общее количество ошибочных переходов - m *(m -1). Отсюда следует, что:
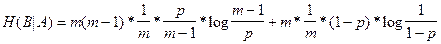 .
.
Следовательно, Н(В/А) не зависит от распределения вероятности в ансамбле А, а определяется только переходными вероятностями канала. Это свойство сохраняется для всех моделей канала с аддитивным шумом.
Максимальное значение Н (В)=log m. Отсюда следует:
 . (4)
. (4)
Пропускная способность в двоичных единицах в расчете на единицу времени:
 . (5)
. (5)
Для двоичного симметричного канала (m=2) пропускная способность в двоичных единицах в единицу времени
С=u[1+p*log(p)+(1-p)*log(1-p)] (6)
Зависимость С/u от р согласно (6) показана на рис.3

рис.3 Зависимость пропускной способности двоичного симметричного канала без памяти от вероятности ошибочного приёма символа.
При р=1/2 пропускная способность канала С=0, поскольку при такой вероятности ошибки последовательность выходных символов можно получить совсем не передавая сигнала по каналу, а выбирая их наугад, т.е. при р=1/2 последовательности на выходе и входе канала независимы. Случай С=0 называют обрывом канала.






