В соответствии с уравнением затухающих колебаний построить графики зависимости угла сдвига и амплитуды колебаний от времени для одного из наблюдений

Задание по обработке результатов

 

1. Статистическая обработка измеренных значений. Определить по данным таблиц 1 и 2 средние значения интервалов времени 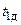, , и . Определить погрешности этих величинс доверительной вероятностью P = 95%.

Таблица 1

N
, c	9,41	9,41	9,56	9,37	9,53
, c	13,40	13,25	13,59	13,28	13,58
, c	54,56	58,03	57,14	55,48	58,31
,c	83,56	85,03	84,44	85,49	84,15

 

Определим средние значения , :

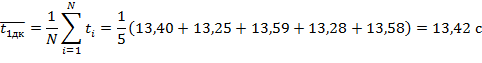
Определим погрешности значений , :

Формула расчета СКО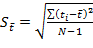

Формула случайной доверительной погрешности результата измерений

Приборная погрешность

Полные погрешности результатов измерений вычисляются по формуле и равны:

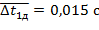
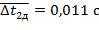
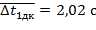
Значит, , равны:

с

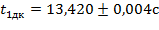
Сведем все вычисленные значения в Таблицу 2

Таблица 2

Среднее значения величины, с	Результат, с

 

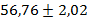
2. Определение периода колебаний маятника. Пользуясь методом переноса погрешностей, для диска без кольца и с кольцом рассчитайте средние значения и полные погрешности периода колебаний .

Проведем расчеты для диска без кольца:

Расчетная формула , где n =10.

Пользуясь значениями, найденными в пункте 1 (Таблица 2), вычислим

Полная погрешность , где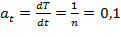

Значит, среднее зачение периода колебания диска без кольца , а полная погрешность периода колебаний составляет 0,0015 с

с

Проведем расчеты для диска с кольцом:

Расчетная формула , где n =10.

Пользуясь значениями, найденными в пункте 1 (Таблица 2), вычислим

Полная погрешность , где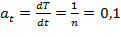

Значит, среднее значение периода колебания диска с кольцом , а полная погрешность периода колебаний составляет 0,2 с.

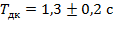
3. Определение момента инерции маятника. Определить момент инерции маятника по формуле

, ,

где – момент инерции кольца. Вычислить погрешность 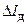, пользуясь правилами расчета погрешностей косвенных измерений. Рассчитать значение момента инерции диска маятника, исходя из его размеров и плотности материала. Сравнить полученный результат с экспериментальным значением.

 

Пользуясь расчетами пунктов 1 и 2 определим среднее значение момента инерции маятника , которое расчитывается по формуле

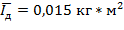
Погрешность измерений момента инерции равна .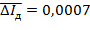

Произведем расчет инерции диска маятника, исходя из его размеров и плотности материала. Расчетная формула , где – плотность материала, - толщина диска маятника, - диаметр диска маятника

4. Определение времени затухания маятника. Пользуясь методом переноса погрешностей, для диска без кольца и с кольцом рассчитайте средние значения и полные погрешности времени затухания t маятника и погрешность Dt при P = 95%. Время затухания вычисляется по формуле

.

Определим время затухания маятника без кольца

Воспользуемся значениями и , расчитаными в пункте 1 (Таблица 2)

Рассчитаем среднее значение времени затухания маятника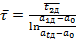

Полная погрешностьвремени затухания маятника без кольца вычисляется по формуле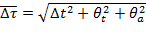

Значит, время затухания маятника без кольца равно с

Определим время затухания маятника с кольцом

Воспользуемся значениям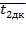и и 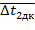, расчитаными в пункте 1 (Таблица 2)

Рассчитаем среднее значение времени затухания маятника

Полная погрешностьвремени затухания маятника с кольцом вычисляется по формуле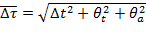

Значит, время затухания маятника с кольцом равно с

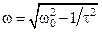5. Определение собственной частоты колебаний гармонического осциллятора. Пользуясь выражениями и , определить собственные частоты и колебаний для диска без кольца и с кольцом. Вычислить их погрешности.

Собственные частоты и можно вычислить по формуле

Погрешность

Погрешность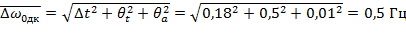

6. Определение коэффициента кручения и модуля сдвига материала подвеса. Найти коэффициент кручения и погрешность D k. Рассчитать среднее значение модуля сдвига G.

Коэффициент кручения можно расчитать по формуле

Расчитаем модуль сдвига 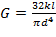, где l – длина подвеса, а d – диаметр подвеса

7. Определение полной энергии, мощности потерь и добротности маятника. Пользуясь соответствующими соотношениями, определить средние значения указанных величин.

Полная энергия маятника W расчитывается по формуле , где A – конечная амплитуда

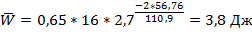
Мощность потерь 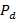расчитывается по формуле

Добротность маятника расчитывается по формуле

В соответствии с уравнением затухающих колебаний построить графики зависимости угла сдвига и амплитуды колебаний от времени для одного из наблюдений.

 

Вывод:

Выполнив данную лабораторную работу, мы провели исследование динамики колебательного движения крутильного маятника.

Сравнив периоды колебаний маятника и время затухания маятника с кольцом и без кольца мы получили, что период маятника с кольцом (с) больше, чем период маятника без кольца (с). Таким образом, мы обнаруживаем зависимость периода колебаний от распределения массы груза на поверхности крутильного маятника относительно оси вращения.