При дифференцировании константу можно выносить за производную: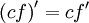 
.
Правило дифференцирования суммы функций: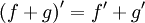 
.
Правило дифференцирования разности функций: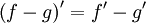 
.
Правило дифференцирования произведения функций (правило Лейбница): 
.
Правило дифференцирования частного функций: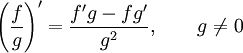 
.
Правило дифференцирования функции в степени другой функции: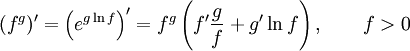 
.
Правило дифференцирования сложной функции: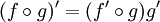 
.
Правило логарифма при дифференцировании функции: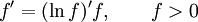 
.
Доказательство первого правила:
Докажем формулу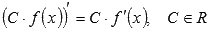 
. По определению производной имеем:
Произвольный множитель можно выносить за знак предельного перехода (это известно из свойств предела), поэтому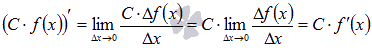 
.
Билет 28.
Применяя теорему о дифференцировании обратной функции, найти производную функции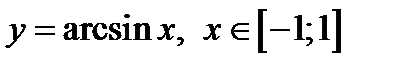 
.
Пусть функция y = f(x) взаимно однозначна в интервале (a, b), содержащем точку x0. Пусть в точке x0 она имеет конечную и отличную от нуля производную f '(x0). Тогда обратная функция x = g(y) также имеет производную в соответствующей точке y0 = f(x0), причем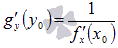 
.
Для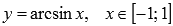 
обратной функцией является 
, тогда по теореме о дифференцировании обратной функции получаем 
(sin2x+cos2x=1 → cos2x=1-sin2x) =
= {cosx=V ̄1-sin2x, xϵ(-π/2; π/2} = 1/V ̄1-sin2x = {x=arcsiny} = 1/V ̄1-sin2(arcsiny) = {sin(arcsiny)=a} = 1/V ̄1-y2. Итак (arcsiny)’ = 1/V ̄1-y2.
Переобозначим независимую переменную y через x и получим arcsinx = 1/V ̄1-x2.
Билет 30.
Доказать теорему Лагранжа.
Если функция f (x) непрерывна на замкнутом отрезке [ a, b ], дифференцируема внутри него, то существует такая точка с Î (a, b), что выполняется равенство f (b) − f (a) = f '(c)·(b − a). Рассмотрим функцию y=f(x)
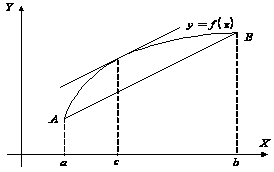
Проведем хорду, соединяющую точки A и B, и запишем ее уравнение. Воспользовавшись уравнением прямой, проходящей через две точки на плоскости, получим:
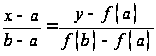, откуда
и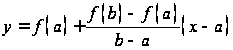 
.
Составим теперь вспомогательную функцию, вычтя из уравнения кривой уравнение хорды:
Вычислим производную функции F(x):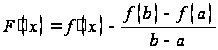 
Согласно теореме Ролля в точке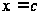 
производная 
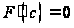, то есть 
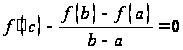и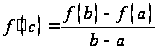 
.
Билет 32.
Сформулировать теорему о дифференцировании сложной функции. Выписать таблицу производных в терминах сложных функций.
Сложная функция – это функция, аргументом которой также является функция.
Пусть функция x = f(t) дифференцируема в точке t, а функция y = f(x) дифференцируема в соответствующей точке x = f(t). Тогда сложная функция y = f(f(t)) дифференцируема в точке t, причем справедлива формула
(f(f(t)))' = f'(x)f'(t).
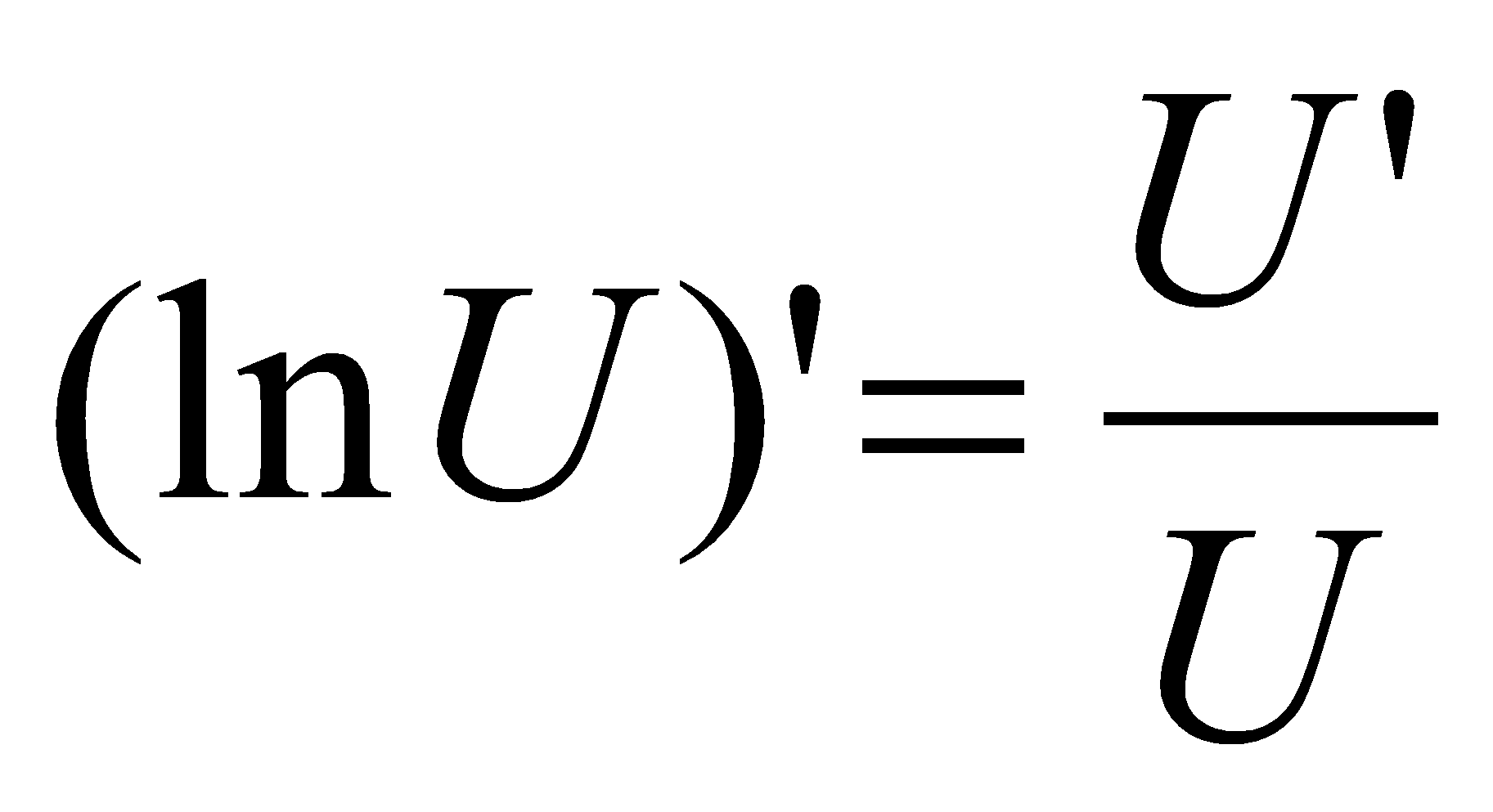
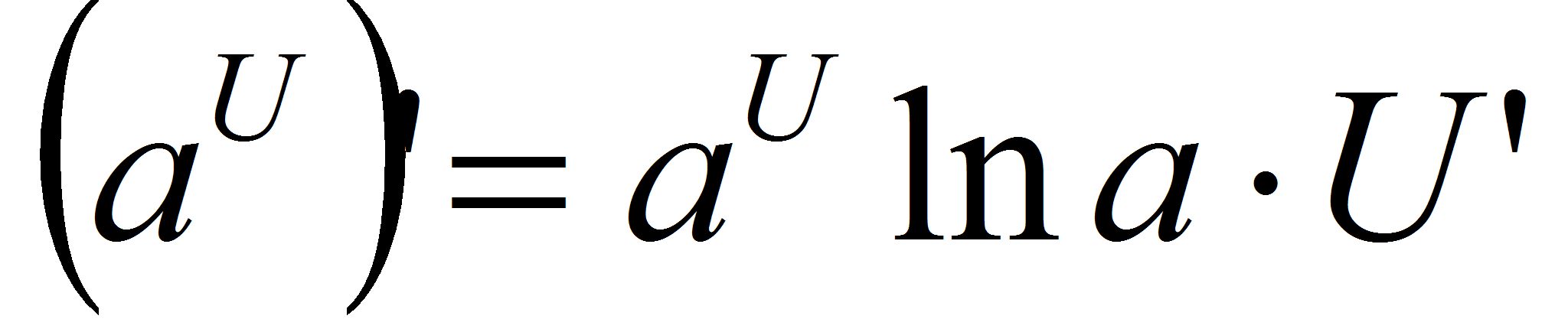
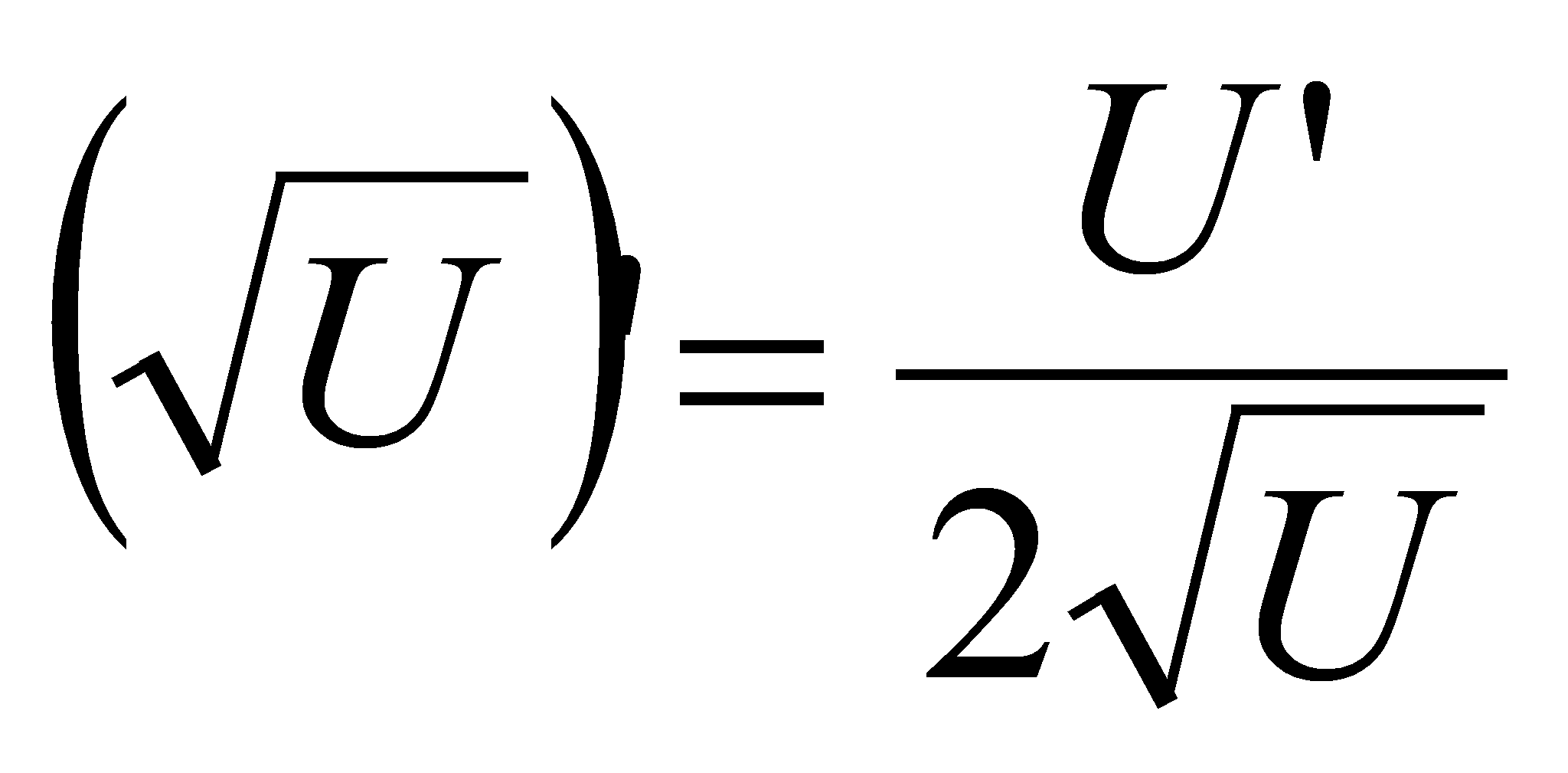
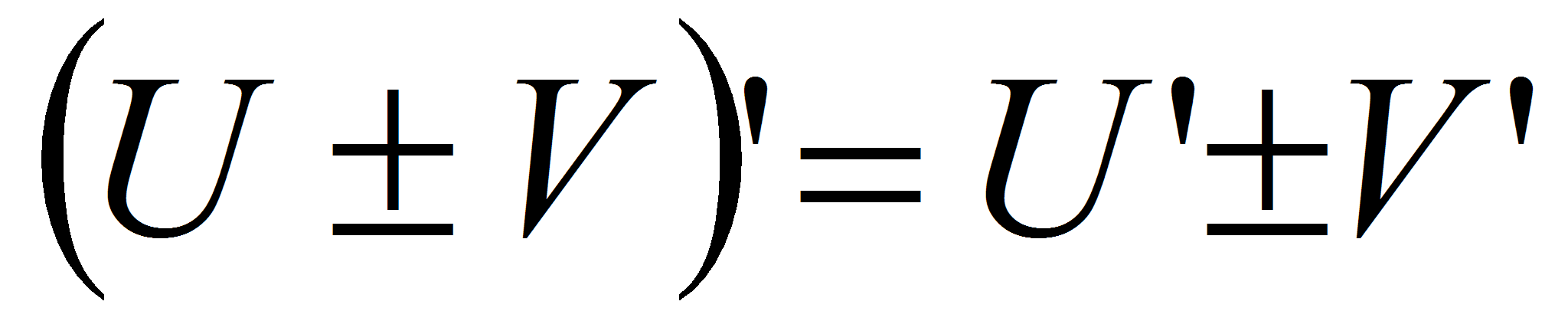
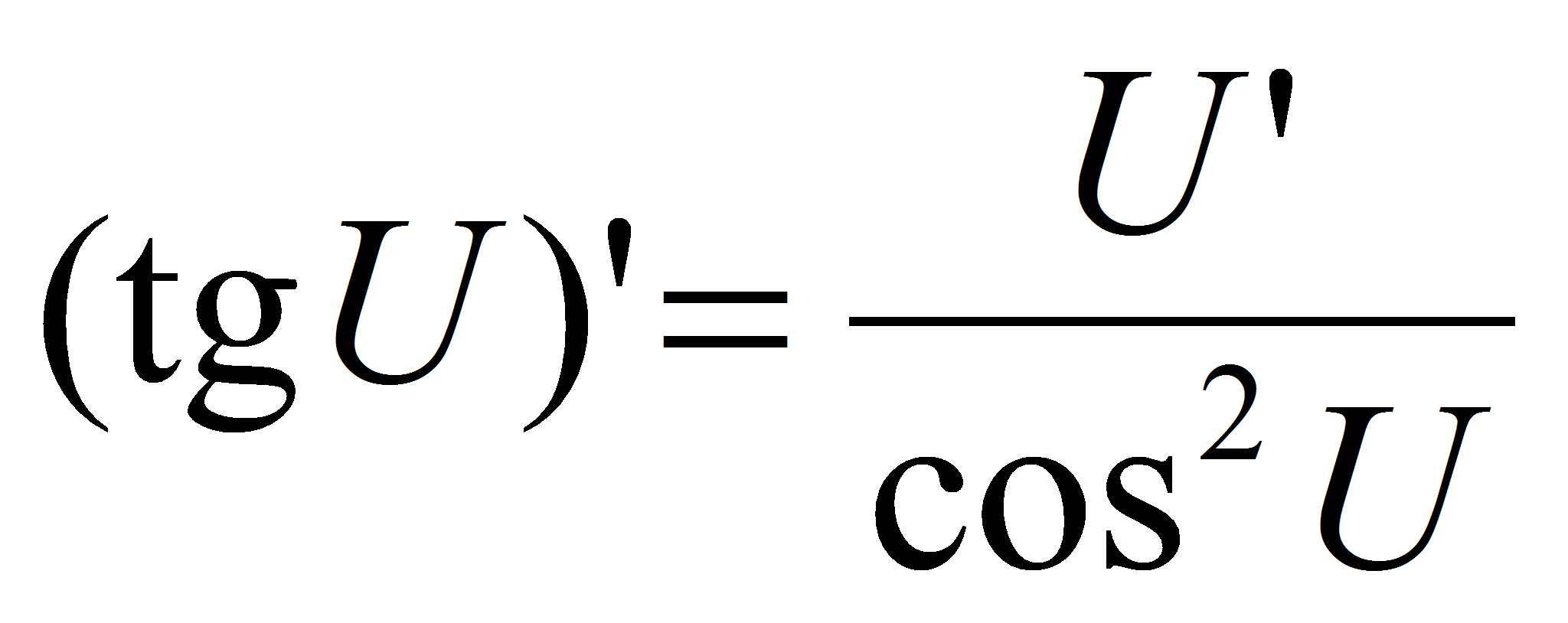
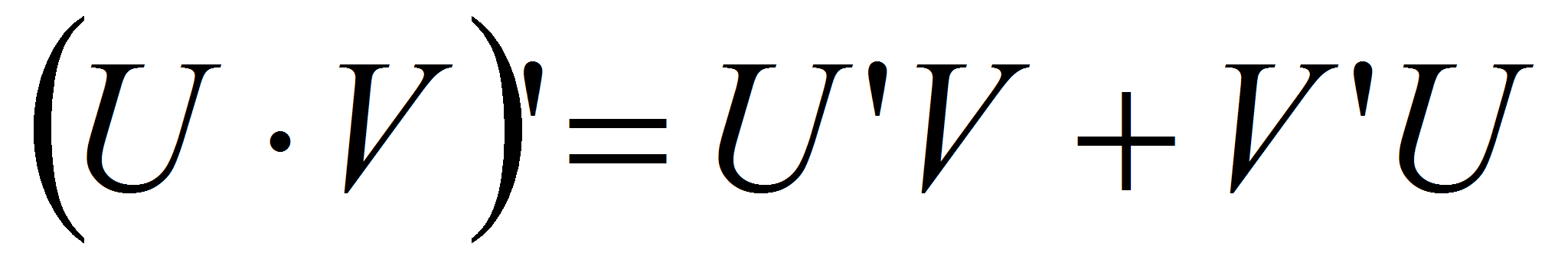
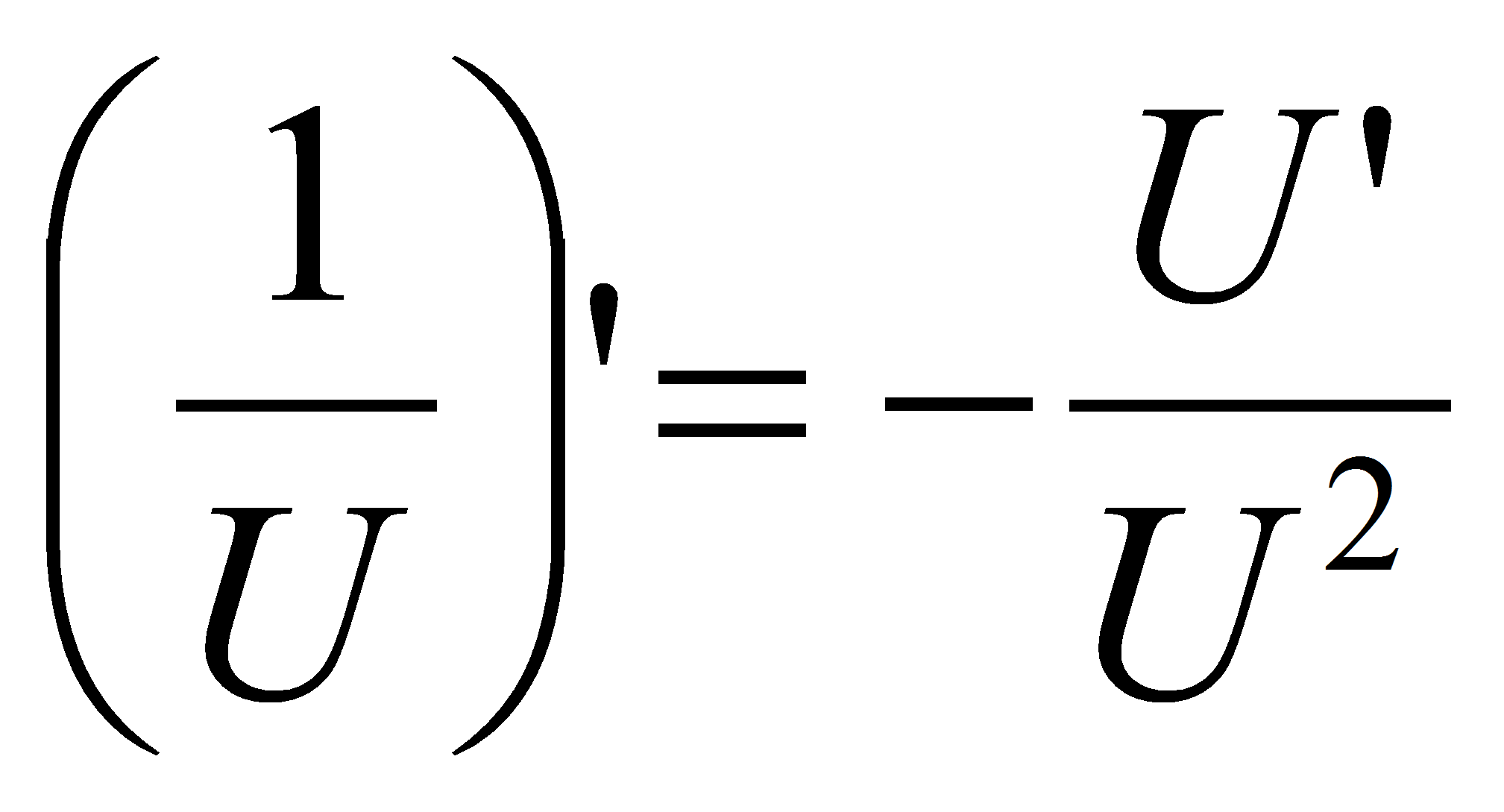
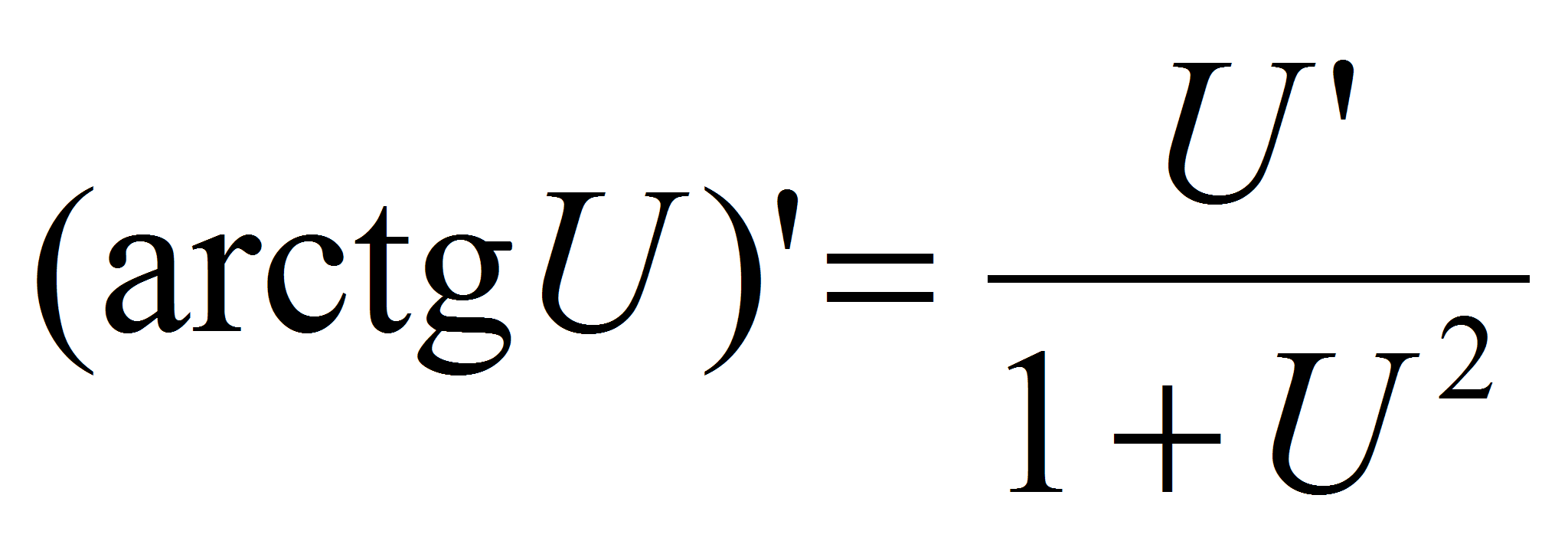
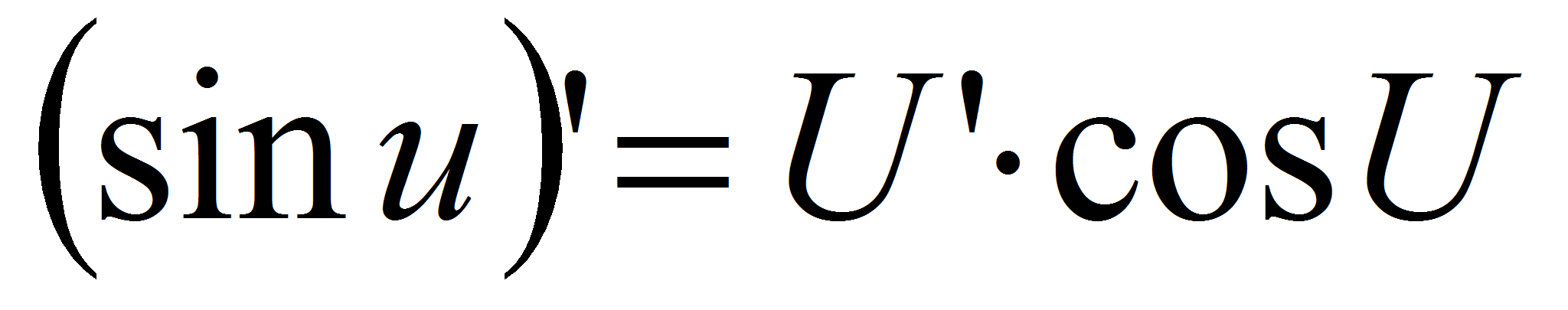
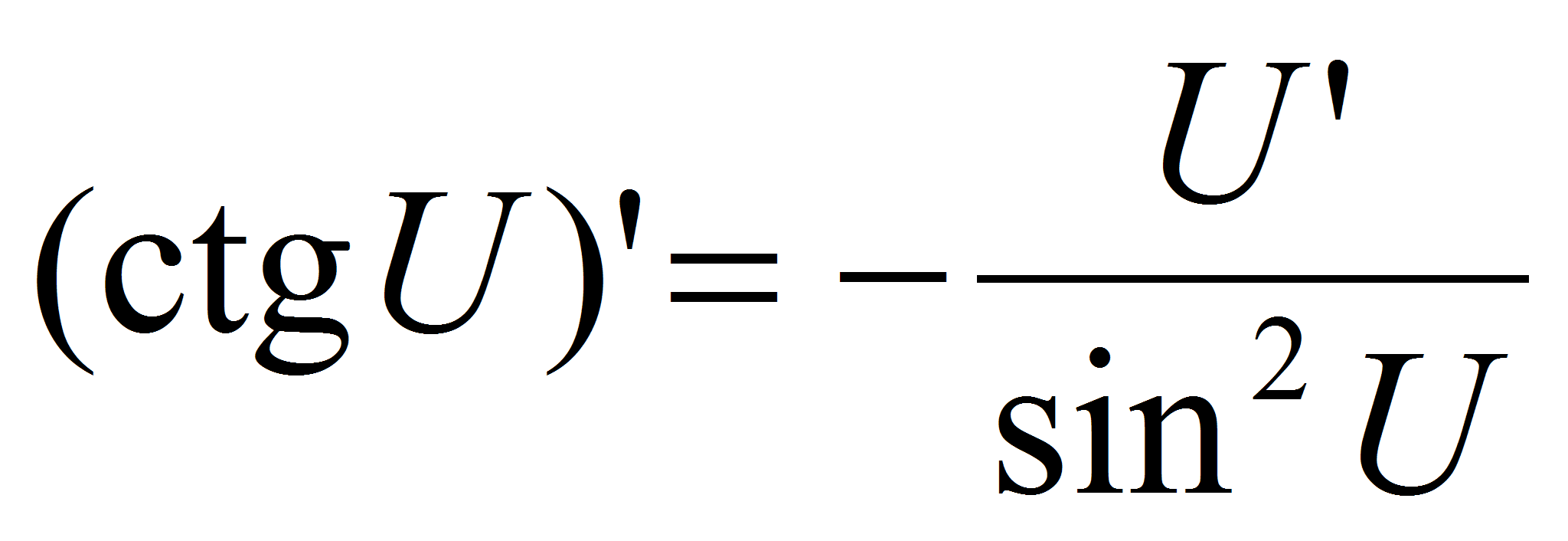
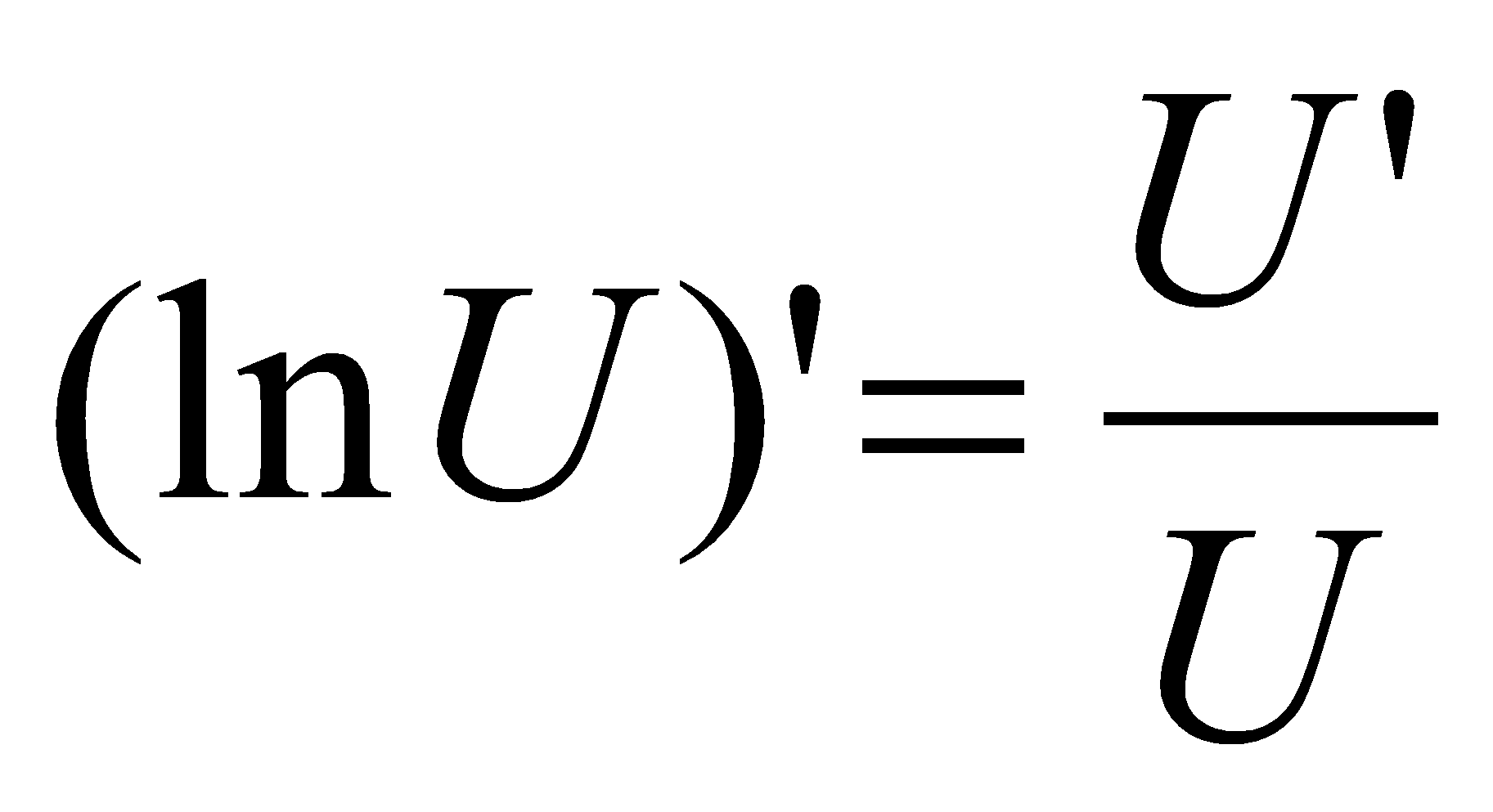
Билет 34.
Дать определение дифференциала функции в точке. Вывести формулу для нахождения дифференциала. Привести пример.
Дифференциалом y=f(x) в точке Х0 называется линейная относительность ∆Х часть приращения функции в точке Х0.
dy = f’(x0)∆x (∆x= dx)
dy = f’(x)dx, где y – функция. → dsinx = dcosxdx
Билет 36.
