Платформа движется по закруглению с линейной скоростью v. Шарик, подвешенный на нити на этой платформе, отклоняется на угол a. Определите радиус R закругления

Ответ: .

Какова должна быть скорость движения мотоциклиста, чтобы он мог описывать горизонтальную окружность на внутренней поверхности вертикального кругового цилиндра радиусом r, если при езде по горизонтальной поверхности с таким же коэффициентом трения скольжения минимальный радиус поворота при скорости v1 равен R?

Ответ: .

Груз, подвешенный на невесомой нити, описывает горизонтальную окружность с постоянной скоростью (конический маятник). Расстояние от точки подвеса до центра окружности равно h. Определите число n оборотов маятника за 1 с.

Ответ: .

2.2.12. Вертикально расположенная пружина соединяет два груза. Масса верхнего груза m ₁ = 2 кг, нижнего m ₂ = 3 кг. Когда система подвешена за верхний груз, длина пружины равна l ₁ = 0,1 м. Если же систему поставить вертикально на подставку, длина пружины равна l ₂ = 4 см. Определите длину l ₀ ненапряженной пружины.

Ответ: .

2.2.13. Шарик подвешен на нити длиной l = 1 м. Шарик расположили так, что он начал двигаться равномерно по окружности в горизонтальной плоскости с периодом T = 1,57 с. При этом угол, образованный нитью с вертикалью, a = p/6 рад. Определите линейную скорость и центростремительное ускорение при движении шарика по окружности.

Ответ: ; .

2.2.14. Определите ускорение тела, соскальзывающего с наклонной плоскости, если угол наклона плоскости a = 30°, а коэффициент трения m = 0,15. Принять g = 10 м/с².

Ответ: .

2.2.15. Бусинка может скользить по обручу радиусом R = 4,5 м, который вращается относительно вертикальной оси, проходящей через его центр и лежащей в плоскости обруча, с угловой скоростью w = 2 рад/с. На какую максимальную высоту h относительно нижней точки обруча может подняться бусинка? Принять g = 10 м/с².

Ответ: .

2.2.16. Через вращающийся вокруг горизонтальной оси блок перекинута нить – невесомая и нерастяжимая, к концам которой привязаны грузы m ₁ = 0,5 кг и m ₂ = 0,6 кг. Определите силу давления F _д блока на ось при движении грузов и ускорение а грузов (массой блока и трением в блоке пренебречь). Принять g = 10 м/с².

Ответ: ; F _д = 2 m ₂(g - a) = 10,9 Н.

2.2.17. На внутренней поверхности сферы радиусом R = 0,1 м, вращающейся вокруг вертикальной оси, находится небольшой предмет. С какой постоянной частотой n должна вращаться сфера, чтобы предмет находился в точке, направление на которую из центра сферы относительно горизонтали составляет угол a = 45°? Коэффициент трения между предметом и поверхностью сферы m = 0,2. Принять g = 10 м/с².

Ответ: .

2.2.18. С какой скоростью движется конькобежец по закруглению ледяной дорожки радиусом R = 10 м, если, проходя этот поворот, он наклоняется к горизонту под углом a = 76°? Принять g = 10 м/с².

Ответ: .

2.2.19. Самолет летит горизонтально с ускорением а. Шарик, подвешенный на нити в самолете, отклоняется от вертикали на угол a. Определите ускорение самолета.

Ответ: а = g ×tga.

2.2.20. Девочка массой m = 35 кг качается на качелях. Длина веревок качелей l = 2 м. Определите силу F _н натяжения веревок в тот момент, когда качели проходят положение равновесия, если максимальная скорость движения v = 3 м/с.

Ответ: .

2.2.21. Космическая ракета движется вертикально вверх с ускорением
a = 5 м/с². Определите вес P космонавта, если его масса m = 75 кг. Принять g = 10 м/с².

Ответ: Р = m (g + a) = 1125 Н.

2.2.22. Автомобиль массой m = 100 кг движется по горизонтальному участку шоссе с ускорением a = 2 м/с². При этом мотор развивает силу тяги F _т = 500 Н. Определите силу сопротивления движению.

Ответ: F _сопр = F _т - ma = 300 Н.

2.2.23. К пружине жесткостью k = 500 Н/м подвесили груз массой
m = 1 кг, при этом длина пружины стала l ₁ = 0,12 м. До какой длины растянется пружина, если к ней подвесить еще один груз массой
m = 1 кг?

Ответ: l ₂ = l ₁ + mg / k» 0,14 м.

2.2.24. На рис. 2.27 представлен график зависимости скорости от времени для поднимающегося вверх лифта. Определите, с какой силой человек массой
m = 60 кг, находящийся в лифте, давит на пол во время его движения. Принять g = 10 м/с².

Ответ: F _д = m (g + Dv/D t) = 576 Н.

2.2.25. Угол a наклона доски к горизонту можно изменять от 0° до 90°. На доску помещен груз, который начинает скользить при значении угла a₀ = 30°. Определите ускорение а груза при его движении по доске, если угол a₁ = 60°.

Ответ: а = g (sina₁ - tga₀×cosa₁) = 5,66 м/с².

2.3.1. Дорожка для велосипедных гонок имеет закругление радиусом R = 40 м. В месте закругления дорожка выполнена с наклоном a = 40° к горизонту. На какую скорость v езды рассчитан такой наклон?

Ответ: .

2.3.2. Мотоциклист участвует в гонках по вертикали и едет по внутренней поверхности вертикального цилиндра радиусом R = 15 м, при этом центр тяжести мотоцикла с человеком расположен на расстоянии
d = 75 см от поверхности цилиндра. Угол наклона мотоциклиста к плоскости горизонта a = 30°. Чему равен коэффициент трения m покрышек колес мотоцикла о поверхность цилиндра? С какой минимальной скоростью v_min должен ехать мотоциклист, чтобы не сорваться со стены? Принять g = 10 м/с².

Ответ: m = tga = 0,58; .

2.3.3. Велосипедист движется по закруглению дороги радиуса
R = 45 м с наибольшей возможной в данных условиях скоростью v_max=15 м/с. (Это предельная скорость, при которой велосипедиста не “заносит”). Определите коэффициент трения скольжения m между шинами и асфальтом, а также угол a отклонения велосипедиста от вертикали, когда он движется по закруглению.

Ответ: ; a = arctgm» 27°.

2.3.4. С какой максимальной скоростью v_max может устойчиво, не опрокидываясь, двигаться вагон по закруглению радиусом R = 150 м, если высота центра масс вагона от уровня рельс Н = 1,8 м, а расстояние между рельсами d = 1,5 м. Принять g = 10 м/с².

Ответ: .

2.3.5. Определите наименьший радиус R круга, по которому сможет проехать велосипедист со скоростью v = 30 км/ч, если коэффициент трения скольжения между колесами и землей m = 0,25. Определите также наибольший угол a наклона велосипеда, при котором велосипедист еще не будет падать. Принять g = 10 м/с².

Ответ: R = v²/(m g) = 27,8 м; a = arctgm = 14°.

2.3.6. Космический корабль совершает мягкую посадку на Луну (ускорение свободного падения вблизи поверхности Луны g _л = 1,6 м/с²). При этом корабль движется равнозамедленно в вертикальном направлении с ускорением a = 8,4 м/с². Определите вес P космонавта массой
m = 70 кг, находящегося в этом корабле.

Ответ: Р = m (g _л + a) = 700 Н.

2.3.7. Определите вес пассажира массой m = 60 кг, находящегося в движущемся лифте, в начале и конце подъема, а также в начале и в конце спуска. Ускорение a (по модулю) лифта для всех случаев считать одинаковым и равным 2,2 м/с².

Ответ: Р = m (g ± a). P ₁ = 720 Н; P ₂ = 456 Н; P ₃ = 456 Н; P ₄ = 720 Н.

2.3.8. С какой силой давит груз массой m = 60 кг на подставку, если подставка вместе с грузом движется вниз равнозамедленно с ускорением а = 1 м/с²? Принять g = 10 м/с².

Ответ: F = m (g + a) = 660 Н.

2.3.9. Определите вес тела массой m =
= 40 кг в положениях А и В (рис. 2.28) если радиусы траекторий в точках А и В равны соответственно R ₁ = 20 м и R ₂ = 10 м, а скорости движения тела в точках А и В равны соответственно v₁ = 10 м/с и v₂ = 5 м/с. Принять g = 10 м/с².

Ответ: ; .

2.3.10. Тело массой m = 2,5 кг движется вертикально вниз с ускорением а = 19,6 м/с². Определите силу F, действующую на тело одновременно с силой тяжести mg во время движения. Сила сопротивления воздуха F _сопр = 10 Н.

Ответ: F = m (a – g) + F _сопр = 34,5 Н.

2.3.11. Через неподвижный блок перекинута нить, к концам которой подвешены два груза массой m ₁ = 200 г. Какой добавочный груз m ₂ нужно поместить на один из висящих грузов, чтобы каждый из них переместился на s = 150 см за t = 5 с.

Ответ: .

2.3.12. Тепловоз тянет состав, состоящий из n = 5 одинаковых вагонов с ускорением а = 10 м/с². Определите силу натяжения сцепки между треть­им и четвертым вагонами (считая от начала состава), если масса каждого вагона
m = 100 кг, а коэффициент сопротивления m = 0,1. Принять g = 10 м/с².

Ответ: F = m (n – k)×(a + m g) = 2200 Н, где k = 3.

2.3.13. Через блок перекинут шнур, к концам которого прикреплены грузы массами m ₁ = 3 кг и m ₂ = 6 кг, рис. 2.29. Блок подвешен к пружинным весам. Определите показание весов при движении грузов (массой блока и шнура, а также трением в блоке пренебрегаем).

Ответ: .

2.3.14. К краям стола (рис. 2.30) прикреплены неподвижные блоки, через которые перекинуты два шнура, привязанные к бруску, массой
m = 3 кг, лежащему на столе. (Силой трения между столом и бруском пренебрегаем). К висящим концам шнуров подвешены гири, массы которых m ₁ = 1,5 кг и m ₂ = 2,5 кг. Определите силу натяжения каждого из шнуров. (Массой блоков и трением в блоках пренебрегаем). Принять g = 10 м/с².

Ответ: F _нат1 = m ₁(g + a) = 17,1 Н; F _нат2 = m ₂(g – a) = 21,5 Н,

где а = g (m ₂ - m ₁)/(m ₁ + m ₂+ m).

2.3.15. На наклонной плоскости находится легкая тележка, которая может скатываться с этой плоскости без трения. На тележке укреплен кронштейн с шариком массой m = 10 г, подвешенным на невесомой и нерастяжимой нити. До начала скатывания нить удерживалась в направ­лении, перпендикулярном к наклонной плоскости. Определите
ускорение а тележки, силу F _нат натяжения нити отвеса при свободном скатывании тележки, если угол наклона плоскости к горизонту a = 30°.

Ответ: а = g ×sina; F _нат = mg ×cosa» 0,085 Н.

2.3.16. На рис. 2.31 изображена система грузов, находящихся в лифте, который движется вверх с ускорением а = 1 м/с². Коэффициент трения между грузом массой m ₂ и столом равен m = 0,1. Определите силу натяжения троса, связывающего грузы, если m ₁ = 1 кг, а m ₂ = 2 кг. Принять g = 10 м/с².

Ответ: 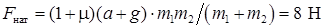, при m m ₂ < m ₁.

2.3.17. По наклонной плоскости скользят два груза массами m ₁ = 1 кг и m ₂ = 2 кг, связанные невесомой нерастяжимой нитью, рис. 2.32. Коэффициенты трения между грузами и плоскостью равны, соответственно: m₁ = 0,7; m₂ = 0,6. Определите силу натяжения нити, если угол наклона плоскости к горизонту a = 30°.

Ответ: .

2.3.18. На наклонной плоскости, угол наклона которой к горизонту составляет b₀ = 25°, лежит тело массой m = 1 кг. Коэффициент трения тела о плоскость m = 0,5. Определите силу F _тр трения, действующую на тело. Определите зависимость силы трения, действующей на тело, от угла наклона b плоскости к горизонту.

Ответ: F _тр = mg ×sinb₀ = 4,14 H;

F _тр(b) = mg ×sinb, при tgb £ m; F _тр(b) = m× mg ×cosb, при tgb > m.

2.3.19. Определите силу F _нат натяжения нити в системе тел, изображенной на рис. 2.33, где
m ₁ = 2 кг; m ₂ = 3 кг; m ₃ = 5 кг. Коэффициент трения между телами 1 и 2 m = 0,2. Угол наклона плоскости к горизонту b = 45°. (Трением между телом 2 и наклонной плоскостью, а также трением в блоке пренебрегаем).

Ответ: .

2.3.20. Определите силы натяжения нитей,
связывающих грузы в системе, изображенной на рис. 2.34. Массы тел соответственно
m ₁ = 1 кг; m ₂ = 2 кг; m ₃ = 4 кг. Коэффициент трения первого тела о наклонную плоскость m₁ = 0,1, коэффициент трения второго тела о наклонную плоскость m₂ = 0,2. Угол наклона плоскости к горизонту a = 30°. (Трением в блоке пренебрегаем). Принять g = 9,8 м/с².

Ответ: ; ,

где .

2.3.21. На платформе, вращающейся с частотой n = 30 об/мин, находится груз массой m = 0,2 кг. Груз прикреплен к центру платформы невесомой абсолютно упругой пружинкой длиной l ₀ = 10 см. При вращении платформы пружинка растягивается на D l = 2 см. Опреде­лите силу F реакции пружины, принимая во внимание максимальную силу трения покоя между грузом и платформой (коэффициент трения
m = 0,09).

Ответ: .

2.3.22. Вертикально расположенная пружина соединяет два груза. Масса верхнего груза m ₁ = 3 кг, нижнего m ₂ = 4 кг. Если эту систему поставить вертикально на подставку, длина пружины равна l ₁ = 3 см. Если же систему подвесить за верхний груз, а к нижнему грузу еще прикрепить груз m ₃ = 1 кг с помощью дополнительной нити, то длина пружины станет l ₂ = равной 12 см. Определите длину l ₀ ненагруженной пружины. Результат представьте в сантиметрах и округлите до целого числа.

Ответ: .

2.3.23. К резиновому шнуру прикреплен шарик массой m = 50 г. Длина шнура в нерастянутом состоянии l = 30 см. Известно, что под влиянием силы, равной F = 9,8 Н, шнур растянется на D l = 1 см. Считая растяжение шнура пропорциональным приложенной силе, определите, на сколько удлинится шнур при вращении шарика с частотой
n = 180 об/мин.

Ответ: , где k = F /D l – жесткость пружины.

2.3.24. Тело массой m = 10 г, прикрепленное к пружине длиной l ₀ = 0,3 м, равномерно вращается в горизонтальной плоскости. При какой частоте вращения пружина удлинится на D l = 0,05 м, если жесткость пружины равна 400 Н/м.

Ответ: .

2.3.25. Шарик массой m, прикрепленный к резиновому шнуру, совершает вращательное движение в горизонтальной плоскости с угловой скоростью w. Длина нерастянутого резинового шнура равна l ₀. Определите радиус окружности R, по которой будет двигаться шарик и силу натяжения F _нат шнура, считая, что при растяжении шнура выполняется закон Гука, т. е. сила натяжения шнура растет пропорционально его растяжению (F _нат = k D l, здесь k – коэффициент жесткости пружины).

Ответ: ; .