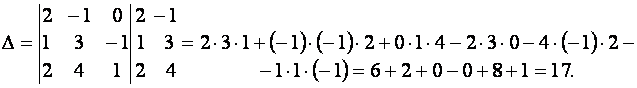КРИВЫЕ ВТОРОГО ПОРЯДКА
Общий вид линии второго порядка:
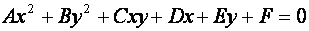 . (1)
. (1)
К кривым второго порядка относятся: окружность, эллипс, гипербола, парабола.
Окружность
Окружность – это множество точек плоскости, равноудаленных от данной точки (центра).
 (2)
(2)
где 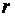 - радиус окружности,
- радиус окружности, 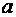 и
и 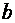 - координаты центра окружности.
- координаты центра окружности.
Если центр окружности совпадает с началом координат, то уравнение имеет вид
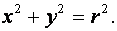 (3)
(3)

Рис. 2
Эллипс
Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (бóльшая, чем расстояние между фокусами).
Каноническое (простейшее) уравнение эллипса с центром в начале координат и с фокусами в точках  и
и 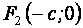 :
:
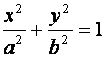 (4)
(4)
где 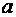 и
и 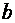 - полуоси эллипса, с – полуфокусное расстояние. Коэффициенты
- полуоси эллипса, с – полуфокусное расстояние. Коэффициенты 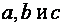 эллипса связаны соотношением
эллипса связаны соотношением 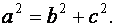
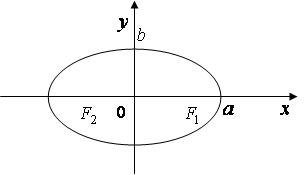
Рис. 3
Если центр эллипса находится в точке 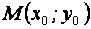 , то уравнение эллипса имеет вид:
, то уравнение эллипса имеет вид:
 (5)
(5)
Гипербола
Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
Уравнение гиперболы с центром в начале координат и с фокусами в точках  и
и 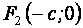 имеет вид:
имеет вид:
 (6)
(6)
где 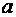 - действительная полуось,
- действительная полуось,
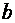 - мнимая полуось.
- мнимая полуось.
Коэффициенты 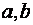 и
и  гиперболы связаны соотношением
гиперболы связаны соотношением 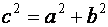 .
.
Прямые 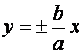 - асимптоты гиперболы.
- асимптоты гиперболы.
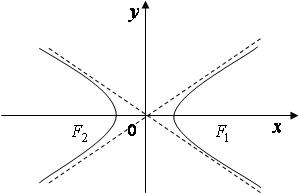
Рис. 4
Если центр гиперболы находится в точке 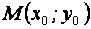 , то уравнение имеет вид:
, то уравнение имеет вид:
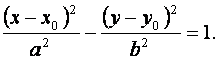 (7)
(7)
Парабола
Параболой называется множество точек плоскости, равноудаленных от точки, называемой фокусом и прямой, называемой директрисой.
Уравнение параболы с вершиной в начале координат имеет вид:
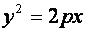 , (8)
, (8)
где  - расстояние между фокусом параболы и прямой линией, называемой директрисой. Фокус параболы имеет координаты
- расстояние между фокусом параболы и прямой линией, называемой директрисой. Фокус параболы имеет координаты  .
.
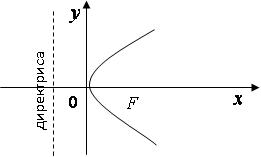
Рис. 5
Если вершина параболы находится в точке 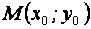 , то уравнение имеет вид:
, то уравнение имеет вид:
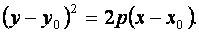 (9)
(9)
Задача 1. Составить уравнение геометрического места точек, равноотстоящего от оси Оу и точки  .
.
Решение: Возьмем на искомой линии произвольную точку 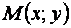 . Расстояние точки М от точки F определится по формуле расстояния между двумя точками:
. Расстояние точки М от точки F определится по формуле расстояния между двумя точками:
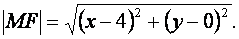
Расстояние точки М до оси Оу определится:

Так как по условию  , то искомая кривая имеет уравнение:
, то искомая кривая имеет уравнение:
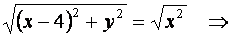
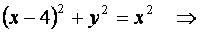
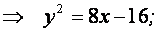
Линия, определяемая полученным уравнением  является параболой.
является параболой.

Задача 2. Составить уравнение геометрического места точек, отношение расстояний которых до точки F (-1; 0) и до прямой х = -9 равно 1/3.
Решение: Возьмём на искомой кривой произвольную точку 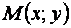 .
.
Её расстояния от точки  и прямой составляют
и прямой составляют 

Из условия задачи следует:

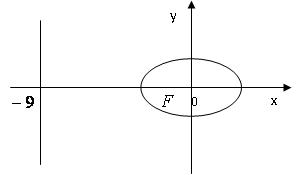
Таким образом, искомая кривая имеет уравнение:
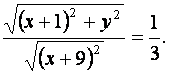
Приведём это уравнение к каноническому виду:
 - это уравнение эллипса с полуосями:
- это уравнение эллипса с полуосями: 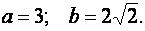
ОПРЕДЕЛИТЕЛИ. МАТРИЦЫ. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Определители
Определитель второго порядка, соответствующий таблице элементов  определяется разностью
определяется разностью 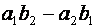 и обозначается:
и обозначается:
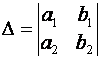
Определитель третьего порядка, соответствующий таблице элементов
 определяется равенством:
определяется равенством:
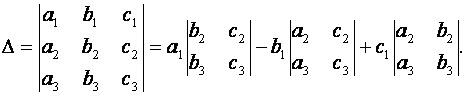
Минором любого элемента определителя третьего порядка называется определитель второго порядка, который получится, если в исходном определителе вычеркнуть строку и столбец, содержащие этот элемент.
Алгебраическим дополнением данного элемента называется его минор, умноженный на 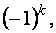 где
где 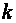 - сумма номеров строки и столбца этого элемента.
- сумма номеров строки и столбца этого элемента.
Определитель третьего порядка можно вычислить диагональным способом. Для этого к определителю последовательно приписываются справа первый и второй столбцы. Произведения элементов, стоящих на главной диагонали, а также на двух параллелях к ней, берутся со знаком плюс; произведения элементов побочной диагонали и на двух параллелях к ней берутся со знаком минус. Алгебраическая сумма этих шести произведений дает определитель третьего порядка



Примеры. Вычислить определители:
а) 
б) 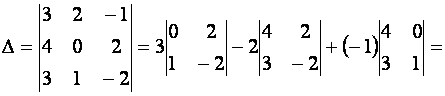
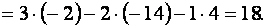
в)