Интерференцией называют явление перераспределения энергии световых волн в пространстве, возникающее при наложении двух или более когерентных волн. В результате интерференции возникает картина, представляющая собой чередование максимумов и минимумов интенсивности света. Устойчивая во времени интерференционная картина наблюдается при наложении когерентных волн. Волны называются когерентными, если разность фаз колебаний, возбуждаемых этими волнами в данной точке пространства, с течением времени не изменяется. Когерентными являются только квазимонохроматические волны, у которых амплитуда, частота и начальная фаза остаются постоянными за время наблюдения.
Две когерентные волны можно получить двумя способами – делением фронта исходной волны и делением ее амплитуды. И в том и в другом случае исходную волну разделяют на две (которые являются когерентными), организуют разность хода и затем сводят их в месте в некоторой области пространства. В результате в этой области возникает интерференционная картина. Важно отметить, что качество наблюдаемой интерференционной картины существенно зависит от степени монохроматичности излучения. Так, в белом свете, имеющим сплошной спектр излучения, наблюдение интерференционной картины практически невозможно из-за того, что максимумы интерференции для одних длин волн накладываются на минимумы интерференции для других длин волн. Поэтому интерференционные картины обычно наблюдают в квазимонохроматическом свете, который получают из белого света с помощью светофильтров.
Получение когерентных волн делением амплитуды реализуется в экспериментальной установке «кольца Ньютона». Интерференционная картина в виде колец Ньютона наблюдаются в случае, когда выпуклая поверхность линзы малой кривизны соприкасается с поверхностью хорошо отполированной пластинки; при этом остающаяся между ними воздушная прослойка постепенно утолщается от центра к краям. Геометрические места точек, соответствующие одинаковой толщине воздушного зазора, являются окружностями.
Разделение исходной квазимонохроматического волны на две когерентные происходит при частичном отражении света от сферической поверхности плоско-выпуклой линзы и от верхней поверхности толстой плоскопараллельной стеклянной пластины (рис.1). Интерференционная картина возникает при наложении этих двух отраженных когерентных волн вблизи сферической поверхности.
Рис. 1. Схема системы линза - подложка
На линзу нормально к плоскости линзы и стеклянной пластины (подложки) падает почти параллельный пучок света. Точка М' – точка падения луча 1 на сферическую поверхность линзы P'ON'. Луч 1 ' формируется в результате отражения луча 1 от сферической поверхности линзы; луч 1 '' – при отражении луча 1 от верхней поверхности стеклянной пластины (подложки) PON. При этом геометрическую разность хода d между лучами 1 ' и 1 '' с достаточной степенью точности можно принять равной 2 d – удвоенной толщине воздушного зазора, так как встреча этих лучей и локализация интерференционной картины произойдет вблизи поверхности P'ОN '.
 |
Определим оптическую разность хода в точках, отстоящих на расстоянии r от оси симметрии, пользуясь схемой, приведенной на рис. 2.
Рис. 2. К расчету оптической разности хода
Из треугольника CO'M' на рис. 1 (точка C – геометрический центр сферической поверхности линзы) находим
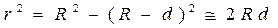. (1)
Здесь R - радиус сферической поверхности линзы, r = O'M'. С учетом условия, что d << R, можно записать r 2 = 2 Rd или 2 d = r 2/ R.
Оптическая разность хода Δ равна разности оптических длин пути лучей 1 ' и 1 '':
Δ = n 2 l 2 – n 1 l 1,
где n 2 = n – показатель преломления среды, находящейся в зазоре между линзой и подложкой (воздух, 
), n 1 – показатель преломления материала линзы (стекла); l 2 – геометрическая длина пути луча 1 ''; l 1 – геометрическая длина пути луча 1 '. Так как l 2 
2 d, а l 1 0 (лучи встречаются вблизи поверхности P'ОN ' см. рис.1), то
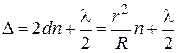, (2)
где λ – длина волны света в вакууме.
Слагаемое l/2в последнем уравнении учитывает дополнительную разность хода, возникающую из-за изменения фазы светового вектора 
волны на величину π при ее отражении от оптически более плотной среды – подложки в точке М.
Как уже было сказано, из осевой симметрии оптической системы следует, что геометрические места постоянной разности хода будут представлять собой систему концентрических колец. Поэтому и наблюдаемая интерференционная картина будет представлять собой чередующиеся светлые и темные кольца, называемые кольцами Ньютона. Кольца Ньютона являются линиями равной толщины.
Следует отметить, что при прохождении света через систему линза-подложка выполняется закон сохранения энергии, поэтому интерференционные картины, наблюдаемые в отраженном и проходящем свете, являются взаимно дополняющими друг друга. В тех местах, где в отраженном свете наблюдается максимум интерференции (светлые кольца), в проходящем свете наблюдается минимум (темные кольца). Однако, если в отраженном свете интерферируют пучки примерно одинаковой интенсивности, то в прошедшем – существенно отличающиеся по интенсивности. Поэтому в проходящем свете интерференционная картина будет значительно менее отчетливой и наблюдение проводят, как правило, в отраженном свете.
Радиусы темных колец определяются условиями интерференционных минимумов
, (3)
где целое число m – порядок интерференционного минимума.
Радиусы светлых определяются условиями интерференционных максимумов
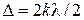, (4)
где целое число k – порядок интерференционного максимума.
Отсюда с учетом (2) и (3) при n = 1 для радиусов темных колец получим
, (5)
а для радиусов светлых колец
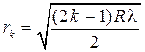. (6)
Здесь m и k = 1, 2, 3... – номера темных и светлых колец.
Для темных колец из (5) следует, что
, (7)
т.е. зависимость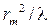 
от номера кольца m является линейной. Это обстоятельство можно использовать для определения радиуса кривизны линзы R, как углового коэффициента уравнения прямой, построенной в соответствующих координатах.
