Введение
Данная работа представляет собой построение нечеткой экспертной системы.
Нечеткая экспертная система – это экспертная система, которая для вывода решения использует вместо булевой логики совокупность нечетких функций принадлежности и правил. Большинство инструментальных средств, работающих с нечеткими экспертными системами позволяют применять в правиле несколько заключений. Нечеткая логика – это надмножество классической булевой логики, расширяющее ее возможности и позволяющее применить концепцию неопределённости в логических выводах. Она была введена Л.Заде как способ моделирования неопределенностей естественного языка. Концептуальное отличие нечеткой логики от классической заключается в том, что она интерпретирует не только значениями «истина» и «ложь», но и промежуточными значениями.
В качестве построения задачи – выбран анализ рейтинга телеканала в зависимости от наличия определенных передач. При выполнении данной работы будет использован метод Сугэно.
Целью работы является ознакомление с нечеткой экспертной системой и анализ вышеупомянутого метода.
Алгоритм Сугэно
Метод Сугэно позволяет работать с большими объемами данных и показывает довольно высокую точность(операция дефаззификации для модели Сугэно проводится по методу «средневзвешанное»).
Сугэно использовал набор правил в следующей форме:
Предположим, что базу знаний образуют два нечётких правила:
П1: если х есть А1 и y есть В1, то z1=a1x+b1y,
П2: если х есть А2 и y есть В2, то z2=a2x+b2y.
1. Первый этап - нечёткость: находятся степени истинности для предпосылок каждого правила: А1(х0), А2(х0), В1(х0), В2(х0)..
2. На втором этапе находятся уровни отсечения для предпосылок каждого правила и индивидуальные выходы правил по формулам:
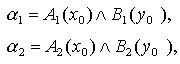
3. На третьем этапе определяется чёткое значение переменной вывода:

Построение нечеткой экспертной системы
Задачей данной работы является определение рейтинга телеканала в зависимости от наличия детских передач и сериалов.
Рассмотрим введенные нами правила:
1. Если сериалов мало(количество передач оцениваться будет по 10балльной шкале), то рейтинг(который оценивается от 0 до 100%), низкий;
2. Если сериалов много и много детских передач, то рейтинг телеканала высокий;
3. Если детских передач мало и примерно средняя частота трансляции, то рейтинг телеканала средний(около 50%).
 |
Рис.1
Входные переменные – это переменные Child(детские передачи) и Serials(сериалы). Используем Гауссово распределение.
Условимся что частота трансляции оценивается по 10балльной шкале(таким образом редкая трансляция - low(0), средняя - middle(5), частая - high(10)).
Выходной переменной является значение рейтинга: низкий(low) – 0%, средний(middle) – 50%, высокий(high) – 100%.

Рис.2
В результате обработки наших условий в программе Matlab, используя метод Сугэно 0-го порядка, мы получили следующие результаты:
| (число сериалов) Serials | (число детских передач) Child | Рейтинг телеканала |
Следует отметить, что при среднем количестве и сериалов и детских передач рейтинг не получился средним(всего 26%), что скорее всего обусловлено наличием погрешностей. Так же можно заметить погрешность при сравнении двух ситуаций: в случае минимального количества и того и другого рейтинг низкий, но не нулевой; при среднем количестве сериалов и минимальном количестве детских передач рейтинг равен нулю.
Вполне гармоничная картина в случае, когда количество сериалов и детских передач равно 7 – рейтинг телеканала высокий(99%).
Затем меняем функции принадлежности. Заменим Гауссовы на треугольные функции.
Рис.3 
Из изображения видно преимущество Гауссовых функций принадлежности над треугольными — так как при Гауссовых функциях принадлежности виден каждый переход в изменении функции.
Заключение
В данной работе было реализовано построение нечеткой экспертной системы. С помощью программы Matlab была создана модель реакции функции в зависимости от установленных нами условий, при выполнении которой был использован метод Сугэно.
При анализе результатов были замечены некоторые отклонения, обусловленные погрешностями, но в целом стоит отметить достаточно высокую точность данного метода.
Список использованной литературы:
1.Дьяконов В. «Математические пакеты расширения Matlab.Справочник»
2.www.intuit.ru






