ЛИНЕЙНЫЕ МОДЕЛИ И ХАРАКТЕРИСТИКИ
СИСТЕМ УПРАВЛЕНИЯ
В разделе рассматриваются различные формы представления конечномерных линейных непрерывных стационарных детерминированных моделей СУ.
В зависимости от информативности о внутренней организации СУ (о ее структуре), выделяют два типа моделей.
 |
Модели первого типа – со “свернутой” внутренней организацией или модели “ вход-выход ” – см. рис. 2.1.
Рис. 2.1
В таких моделях отсутствует информация о внутренней структуре СУ, то есть о составе функциональных звеньев и переменных и о взаимосвязях между ними. Модель представляет собой заданный в некоторой форме математический оператор преобразования входного сигнала f (управляющего или возмущения) в выходной сигнал y.
На таких моделях и рассматриваются в данном разделе формы представления оператора преобразования w.
Модели второго типа – с раскрытой внутренней организацией – несут информацию о структуре системы – см. подразд. 2.5, 2.6.
Дифференциальные уравнения
Дифференциальное уравнение (ДУ) “ n -го порядка” связывает между собой во временной области входную переменную f (t), выходную переменную y (t) и их производные:
. (2.1)
Порядок n определяется по наибольшему номеру производной левой части уравнения.
ДУ дополняется начальными условиями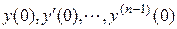 
.
Часто используется компактная запись ДУ, для чего вводится символьный оператор дифференцирования по времени p º d / dt:
An (p) y (t) = Bm (p) f (t), (2.2)
где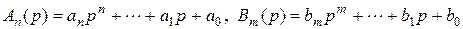 
- оператор-ные полиномы.
Передаточные функции
По определению передаточная функция (ПФ) представляет собой оператор, равный отношению изображения выходной координаты к изображению входной координаты при нулевых начальных условиях. Таким образом, для представленной на рис. 1.1 СУ, ПФ
. (2.3)
Здесь и в дальнейшем будем обозначать изображения функций прописными буквами.
ПФ может быть легко получена из ДУ (2.1). Для этого преобразуем по Лапласу левую и правую части (2.1); при этом воспользуемся свойством линейности преобразования Лапласа и тем его свойством, что дифференцированию оригинала соответствует умножение изображения на комплексный аргумент s (справедливо при нулевых начальных условиях).
Таким образом, если 
В результате получим:
. (2.4)
С учетом (2.3)
. (2.5)
Таким образом, ПФ является дробно-рациональной функцией (отношением двух полиномов). Полиномы числителя и знаменателя образуются из соответствующих коэффициентов правой и левой частей исходного ДУ (2.1) или (2.2). Полином An (s) знаменателя ПФ системы (или отдельного звена) называется характеристическим полиномом системы (звена).
Как видно из (2.1) и (2.5), по ДУ можно сразу записать ПФ, и - наоборот.
Форма представления ПФ (2.5) называется полиномиальной. Можно представить ПФ также в факторизованной форме, то есть коэффициентом, множеством нулей (корней полинома числителя) zj: j =1,…, m, и множеством полюсов (корней полинома знаменателя) pi: i =1,…, n:
. (2.6)
Здесь k = bm / an – отношение старших коэффициентов полиномов (2.5).
Временные характеристики
Реакция любой динамической системы на входной сигнал – временная характеристика – определяется двумя составляющими: параметрами сигнала и свойствами собственно самой системы.
Для рассматриваемых здесь СУ, описываемых линейными дифференциальными уравнениями (2.1), это обстоятельство проявляется в форме решения ДУ, использующей операторный метод на основе преобразования Лапласа. Как следует из (2.3), изображение выходной координаты Y (s)= F (s) W (s). Тогда оригинал – решение ДУ – может быть получен применением обратного преобразования Лапласа:
y (t) = L -1{ Y (s)}. (2.7)
Решение ДУ может быть сведено к сумме двух составляющих:
y (t) = yсв (t) + yвын (t). (2.8)
Свободная составляющая yсв (t) характеризует динамику собственно самой системы и определяется решением однородного уравнения, образующегося из (2.1) приравниванием нулю правой части. При этом решение определяется корнями si: i =1,…, n характеристического полинома (или, что тоже самое, полюсами ПФ) системы:
. (2.9)
Вынужденная составляющая определяется уже с учетом входного сигнала.
В подразд.1.4 введено понятие устойчивости ОУ и СУ с позиции их поведения. Теперь можно записать, что для устойчивости СУ должно выполняться
. (2.10)
Если все n корней характеристического полинома действительные, то yсв (t) представляет собой сумму n экспонент - см. (2.9). Если среди корней имеются пары комплексно-сопряженных корней то каждой такой паре si,i+ 1=a±jw в переходном процессе соответствует составляющая Cie a t Cos(w t).
Если расположить все корни характеристического полинома на комплексной плоскости, то с учетом (2.10) можно сформулировать следующее утверждение.
Для устойчивости СУ необходимо и достаточно, чтобы корни характеристического полинома принадлежали левой полуплоскости плоскости корней.
Если корни действительные, то они должны быть отрицательными, а если есть пары комплексно-сопряженных корней, то должны быть отрицательными их действительные части.
При наличии пары чисто мнимых корней si,i+ 1= ±jw (корни располагаются на оси мнимых) в переходном процессе присутствует незатухающая колебательная составляющая; система находится на колебательной границе устойчивости.
Если имеется хотя бы один “правый” действительный корень или пара комплексно-сопряженных правых корней, то будет иметь место
, (2.11)
что является достаточным условием для неустойчивости СУ.
Если получено изображение процесса Y (s), то еще до нахождения оригинала y (t) могут быть получены предельные значения в начале процесса и по его окончании. Для этого можно воспользоваться теоремами преобразования Лапласа о начальном и конечном значениях оригинала и изображения.
, (2.12)
. (2.13)
Информация о корнях характеристического полинома и соотношения (2.12) и (2.13) позволяют сделать ряд качественных и количественных суждений о характере временной характеристики еще до построения собственно всего переходного процесса в СУ.
Частотные характеристики
Частотные характеристики (ЧХ) представляют собой зависимости установившихся реакций системы (объекта) на гармонические сигналы всех частот. Если на вход некоторой линейной устойчивой СУ подать сигнал Af Sin(w it), то на ее выходе после окончания переходного процесса установятся вынужденные движения, которые также будут представлять собой гармонический сигнал Ay (w i)Sin(w it+ j(w i)) той же частоты, но измененной амплитуды и сдвинутый по фазе. Отношение Ay (w i)/ Af представляет собой коэффициент передачи по амплитуде на данной частоте R (w i), который называется модулем ЧХ.
В ЧХ, используемых для расчетов СУ, частота w - круговая; имеет размерность рад/с (иногда условно обозначается “с-1”).
ЧХ может быть описана оператором W (j w) – комплексной функцией вещественного аргумента w. В соответствии с различными формами представления комплексных чисел используют различные типы ЧХ:
W (j w)=Re(w)+ j Im(w)= R (w) ej j(w). (2.14)
Амплитудно-фазовая характеристика (АФХ) W (j w)=Re(w)+ j Im(w) есть сумма вещественной и мнимой частей ЧХ и строится на комплексной плоскости. При изменении частоты w от нуля до µ конец вектора описывает на комплексной плоскости траекторию, называемую годографом Найквиста. Отдельной оси частот АФХ не имеет и каждая точка характеристики может быть оцифрована соответствующим значением частоты.
Амплитудно-частотная характеристика (АЧХ) R (w), где
, (2.15)
представляет собой зависимость модуля ЧХ от частоты.
Часто используются логарифмические амплитудно-частотные характеристики (ЛАЧХ)
L (w) = 20 lg R (w), (2.16)
где L (w) – логарифмический модуль, измеряемый в децибелах (дБ). При делении оси частот на декады (интервалы десятикратного изменения частоты) и распределении w внутри интервалов в логарифмическом масштабе, ЛАЧХ приобретают ряд специфических особенностей, облегчающих их построение и позволяющих более наглядно отображать свойства СУ.
Фазо-частотная характеристика (ФЧХ) j(w), где
. (2.17)
Как правило, ФЧХ строится одновременно с АЧХ или ЛАЧХ на единой шкале частот; именно соотношение амплитудной и фазовой характеристик позволяет выявить ряд важных свойств СУ.
Если известна ПФ W (s) отдельного звена или всей СУ, то частотный оператор получается простой заменой переменной
. (2.18)
Так как ПФ является отношением двух полиномов комплексного аргумента s, то при подстановке конкретного значения частоты четные степени полиномов дают вещественные части, а нечетные степени – мнимые части ЧХ. Путем избавления от иррациональности в знаменателе ПФ, могут быть выделены вещественная и мнимая части ЧХ, а затем отдельно модуль и фаза.
