Особенностью реальных углеводородных газов по сравнению с идеальным газом является их отклонение от уравнения Менделеева-Клапейрона.
Идеальный газ удовлетворяет данному уравнению в виде:
, (7.8)
где R - газовая постоянная для газа с молекулярной массой М, связанная с универсальной газовой постоянной 
зависимостью
.
Для реального газа уравнение (7.8) приобретает вид:
.
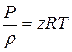Если пластовое давление выше 10 МПа и депрессия не слишком мала (Рс/Рк£0,9), то уравнение состояния природного газа также значительно отличается от уравнения состояния идеального газа. Плотность в этом случае определяется по формуле:
- уравнение состояния реального газа.
В данных уравнениях z – коэффициент свержсжимаемости, характери-зующий степень отклонения состояния реального газа от закона идеального газа. Значения z определяются по графику Д.Брауна (рис. 7.1) в зависимости от приведенных величин абсолютного давления Pr и температуры Tr:
, 
.
Здесь Pср.кр. и Тср.кр. – соответственно среднекритическое давление и среднекритическая температура, определяемые с учетом компонентного состава реального (природного) газа:
, 
,
где nj – содержание j -ого компонента (метана, этана, пропана и т.д.) в газе, % об.; Ркр.j, Ткр.j - критические давление и температура j -го компонента.
Кроме учета компонентного состава газа, при высоких давлениях необходимо принимать во внимание зависимость вязкости от давления.
Случай I. Приток реального газа к совершенной скважине
по линейному закону фильтрации
Функция Л.С.Лейбензона запишется в виде:
.
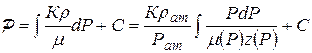Дебит скважины определится по формуле:
,
где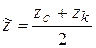 
, 
- среднепластовые значения коэффици-ентов сверхсжимаемости и вязкости, определяемые с помощью графиков зависимостей z(P) и m(Р).
Случай II. Приток реального газа к совершенной и несовершенной скважине по двучленному закону фильтрации
Уравнение притока реального газа по двучленному закону фильтрации к совершенной скважине имеет вид:
.
Круговой пласт, в центре которого находится несовершенная скважина, делится на три области.
В области с радиусом R1»(2-3)rc вблизи перфорационных отверстий проявляется несовершенство по характеру вскрытия, и поток вблизи каждого отверстия близок к радиально-сферическому.
Во второй области (R1 < r £ R2, причем R2 » h) линии тока искривля-ются из-за несовершенства скважи-ны по степени вскрытия.
В первой и второй областях фильтрация газа происходит по двучленному закону.
В третьей области (R2 < r £ Rk) действует закон Дарси, и движение можно считать плоскорадиальным.
Находя разности давлений на границах областей и суммируя полученные выражения, в итоге получим:
(7.9)
где 
и 
определяются по формулам:
;
(при b>>R1);
,
где N – число отверстий; R0 – глубина перфорационного отверстия.
С2 находится по графикам В.И.Щурова.
Уравнение (7.9) является уравнением притока реального газа к гидродинамически несовершенной скважине.
Контрольные вопросы:
1. Приведите выражение и охарактеризуйте свойства функции Л.С.Лейбензона.
2. Как, пользуясь аналогией между фильтрацией несжимаемой жидкости и движением газа, получить уравнения распределения давления, дебита и скорости фильтрации газового потока?
3. В чем заключаются отличия реальных углеводородных газов от идеального газа? Что характеризует коэффициент сверхсжимаемости?
4. Сравните и проанализируйте основные характеристики прямолинейно-параллельного и плоскорадиального фильтрационных потоков газа.
5. Сопоставьте уравнения притока идеального и реального газа к совершенной скважине по линейному закону фильтрации.
6. Сопоставьте уравнения притока идеального и реального газа к совершенной скважине по двучленному закону фильтрации.
7. Сопоставьте уравнения притока реального газа к совершенной и несовершенной скважине по двучленному закону фильтрации.
