| Номер предприятия | Чистая прибыль, тыс. руб. | Численность обслуживаемого населения, млн. чел | Рентабельность, % |
| у | х1 | х2 | |
| 4,9 | |||
| 5,1 | |||
| 6,5 | |||
| 3,7 | |||
| 4,0 | |||
| 2,5 |
В качестве результативного признака возьмем чистую прибыль у. Основные факторы, влияющие на ее формирование: численность населения, обслуживаемого предприятием электросвязи х1, и рентабельность х2 Линейная форма зависимости между признаками постулируется, и, следовательно, задача сводится к отысканию параметров уравнения:
 .
.
При линейной форме связи множественный корреляционно-регрессионный анализ проводится на основе информации о средних значениях признаков  , их средних квадратических отклонениях
, их средних квадратических отклонениях  и парных коэффициентах корреляции
и парных коэффициентах корреляции  .
.
Построим уравнение двухфакторной регрессии в стандартизированном масштабе и рассчитаем показатели тесноты связи (табл. 2.2).
Таблица 2.2
Расчетная таблица для определения параметров уравнения регрессии
| у | х1 | х2 | (х1)2 | (х2)2 | х1 х2 | у х1 | у х2 | у2 |
| 4,9 | 24,0 | |||||||
| 5,1 | 26,0 | |||||||
| 6,5 | 42,3 | |||||||
| 3,7 | 13,7 | |||||||
| 4,0 | 16,0 | |||||||
| 2,5 | 6,3 | |||||||
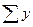 = = 960 = = 960
|  = 26,7
= 26,7
|  = 117
= 117
|  = 128,3
= 128,3
|  = 2411
= 2411
|  = = 501 = = 501
|  = 4419 = 4419
|  = 19537
= 19537
|  = =173646 = =173646
|
Используя итоги расчетной таблицы (см. табл. 2.2) и известные формулы для расчета средних, дисперсий и парных коэффициентов корреляции:


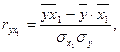
 ,
,  .
.
вычислим показатели, необходимые для отыскания 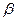 -коэффициентов:
-коэффициентов:
 = 160 тыс. руб.,
= 160 тыс. руб.,  у = 57,8 тыс. руб.;
у = 57,8 тыс. руб.;
 = 4,45 млн. чел.,
= 4,45 млн. чел.,  = 1,2513 млн. чел.;
= 1,2513 млн. чел.;
 = 19,5%,
= 19,5%,  = 4,6458%;
= 4,6458%;
 0,3392,
0,3392,  0,5071,
0,5071,  - 0,5806.
- 0,5806.
Система нормальных уравнений в стандартизированном виде может быть записана так:

Решая эту систему, находим:  = 0,9558,
= 0,9558, 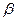 2 = 1,062. Таким образом, можно записать уравнение регрессии в стандартизированном виде:
2 = 1,062. Таким образом, можно записать уравнение регрессии в стандартизированном виде:
ty = 0,9558t1 + 1,062t2.
Коэффициенты при tj показывают, что большее воздействие на чистую прибыль предприятия электросвязи оказывает рентабельность (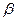 2 >
2 >  ). С ее ростом на сигму при постоянной численности обслуживаемого населения чистая прибыль увеличивается на 1,062 своего среднего квадратического отклонения.
). С ее ростом на сигму при постоянной численности обслуживаемого населения чистая прибыль увеличивается на 1,062 своего среднего квадратического отклонения.
Переход от стандартизированного уравнения регрессии к уравнению регрессии в натуральном масштабе осуществляется по формулам:
 .
.
Найдем параметры искомого уравнения:
 ;
;
 ;
;
 .
.
Уравнение зависимости чистой прибыли предприятий электросвязи от численности обслуживаемого населения и рентабельности имеет вид:

Оно показывает, что с ростом численности обслуживаемого населения на 1 млн. чел., при исключении влияния второго фактора (рентабельности), чистая прибыль возрастает на 44,15 тыс. руб., а при неизменной численности населения с ростом рентабельности на 1% чистая прибыль повысится на 13,21 тыс. руб.
Коэффициент множественной детерминации для нашего примера окажется равным:
 =0,8627.
=0,8627.
Отсюда коэффициент множественной корреляции  .
.
Полученные значения коэффициентов множественной корреляции и детерминации, близкие к 1, свидетельствуют о том, что при построении двухфакторной модели учтены важные факторы увеличения чистой прибыли. При дополнительном включении факторов в анализ (для данного числа предприятий) может увеличиться совокупный коэффициент детерминации и, соответственно, уменьшиться остаточная дисперсия, доля которой в нашем примере мала:
 0,8627 = 0,1373.
0,8627 = 0,1373.
Следовательно, на долю неучтенных факторов приходится не более 13,73% дисперсии результативного признака.
Эластичность по каждому фактору и по их совокупности составит:


 =2,84.
=2,84.
Эластичность по каждому фактору и в целом по совокупности больше 1, значит, чистая прибыль увеличивается в большей степени, чем факторы. С увеличением каждого фактора на 1% следует ожидать увеличения чистой прибыли на 2,84%.
Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии оценивается с помощью F -критерия:
 ,
,
где  ‒ факторная сумма квадратов на одну степень свободы;
‒ факторная сумма квадратов на одну степень свободы;
 ‒ остаточная сумма квадратов на одну степень свободы;
‒ остаточная сумма квадратов на одну степень свободы;
R2 ‒ коэффициент (индекс) множественной детерминации;
n – число наблюдений;
m – число параметров при переменных х (в линейной регрессии совпадает с числом включенных в модель факторов).
Величина Fтабл находится по таблицам при заданном уровне значимости  и числе степеней свободы
и числе степеней свободы  Если Fрасч › Fтабл, уравнение признается статистически значимым.
Если Fрасч › Fтабл, уравнение признается статистически значимым.
Ввиду корреляции между факторами значимость одного и того же фактора может быть разной в зависимости от последовательности включения в модель фактора. Мерой для оценки включения фактора в модель служит частный F -критерий:
 ,
,
где  ‒ коэффициент множественной детерминации для модели с полным
‒ коэффициент множественной детерминации для модели с полным
набором факторов;
 ‒ тот же показатель, но без включения в модель фактора хk.
‒ тот же показатель, но без включения в модель фактора хk.
В случае превышения значения частного F -критерия значения табличного делается вывод о целесообразности включения фактора в модель.
Для оценки значимости каждого коэффициента регрессии необходимо рассчитать значение t- критерия Стьюдента (отношение коэффициента регрессии к его средней ошибке):
 .
.
Коэффициент регрессии считается статистически значимым, если  превышает
превышает 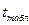 — табличное (теоретическое) значение t -критерия Стьюдента для заданного уровня значимости
— табличное (теоретическое) значение t -критерия Стьюдента для заданного уровня значимости  и п – m – 1 степени свободы.
и п – m – 1 степени свободы.
Бывает необходимо включить в модель качественный (атрибутивный) фактор (факторы). Примером качественных признаков может служить пол, образование, климатические условия.
Чтобы ввести такие признаки в модель, они должны быть преобразованы в количественные, т.е. им должны быть присвоены цифровые метки. Сконструированные на основе качественных факторов числовые переменные называют фиктивными переменными.
Так для построения уравнения регрессии, в котором результативным показателем является заработная плата рабочего за месяц, а объясняющими факторами: возраст рабочего и пол; необходимо ввести
в модель:  фиктивную переменную z, которая принимает 2 значения: 1 – если пол рабочего мужской; 0 – если пол женский.
фиктивную переменную z, которая принимает 2 значения: 1 – если пол рабочего мужской; 0 – если пол женский.
Построим модель: 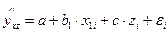 .
.
Для оценки параметров модели используем МНК с системой нормальных линейных уравнений:

В рассмотренном примере качественный признак принимает только 2 значения. Если же градаций качественного признака больше 2, в модель вводится несколько фиктивных переменных. При введении в модель фиктивной переменной действует принцип: число фиктивных переменных должно быть на 1 меньше числа градаций качественного фактора.
Например, при наличии качественного фактора «образование», принимающего значения: до 8 классов, среднее, специальное, необходимо использовать две фиктивные переменные (табл. 2.).
Таблица 2
| Образование | z1 | z2 |
| До 8 классов | ||
| Среднее | ||
| Специальное |
При оценке параметров уравнения регрессии применяется метод наименьших квадратов. При этом делаются определенные предпосылки относительно случайной величины  . В модели:
. В модели:

случайная составляющая представляет собой ненаблюдаемую величину. После того как проведена оценка параметров модели, рассчитав разности фактических и теоретических значений результативного признака можно определить оценки случайно составляющей  . При изменении спецификации модели, добавления в нее новых наблюдений выборочные оценки остатков
. При изменении спецификации модели, добавления в нее новых наблюдений выборочные оценки остатков  могут меняться. Поэтому в задачу регрессионного анализа входит не только построение самой модели, но и исследование случайных отклонений.
могут меняться. Поэтому в задачу регрессионного анализа входит не только построение самой модели, но и исследование случайных отклонений.
Исследование остатков предполагает проверку наличия следующих пяти предпосылок МНК:
- случайный характер остатков;
- нулевая средняя величина остатков, не зависящая от хi;
- гомоскедастичность – дисперсия каждого отклонения одинакова для всех значений х;
- отсутствие автокорреляции остатков;
- остатки подчиняются нормальному распределению.
Первые две предпосылки проверяются графически. Третья предпосылка при малом объеме выборки может проверена с помощью метода Гольфельда-Квандта.
Параметрический тест включает следующие шаги:
1. Все n наблюдений в выборке упорядочиваются по возрастанию переменной х.
2. Исключаются из рассмотрения С центральных наблюдений; при этом (n-C)/2>p, p – число оцениваемых параметров.
3. Разделение совокупности из (n-C) наблюдений на две группы и определение по каждой из групп уравнений регрессии.
4. Определяется остаточная сумма квадратов для первой S1 и второй групп S2 и находится соотношение F= S1/ S2. Если верна гипотеза Н0 об отсутствии гетероскедастичности, то F имеет распределение Фишера с (n-C-2p)/2 степенями свободы, где p – число объясняющих переменных. По таблице определяются критическое значение критерия Fкр. Если F›Fкр, то нулевая гипотеза об отсутствии гетероскедастичности отклоняется.
Последствия гетероскедастичности:
- оценки параметров уравнения регрессии становятся неэффективными;
- оценки стандартных ошибок параметров регрессии будут неверными. (Например, оценки стандартных ошибок могут оказаться заниженными. Тогда значения t -критерия – завышенными. Мы решим, что параметр регрессии значим, а на самом деле это будет не так и сделаем неправильные выводы о значимости уравнения регрессии.)
Таким образом, нами рассмотрена технология построения многофакторной эконометрической модели, показатели, характеризующие ее адекватность и возможность использования для прогнозирования. Рассмотрена также возможность включения в модель качественного фактора путем ввода фиктивной переменной, так как в экономических и социальных процессах не все факторы носят количественный характер.






