Унарной операцией или одноместной операцией на множестве M называется отображение множества в себя M→M, которое каждому элементу множества M, называемому операндом, ставит в соответствие некоторый элемент того же множества, называемый результатом.
Унарную операцию принято обозначать знаком действия, который ставится перед или над операндом. Например, для унарной операции «?» результат её применения к элементу x записывается в виде - x.
Пусть A,B,C — тройка непустых множеств. Бинарной операцией или двуместной операцией в паре A, B со значениями в C называется отображение P→C, где 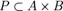
Если A = B = C, то действие называется внутренним, если A = C или B = C — внешним. В частности, любое внутреннее действие является внешним.
Бинарную операцию принято обозначать знаком действия, который ставится между операндами (инфиксная форма записи). Например, для произвольной бинарной операции ○ результат её применения к двум элементам x и y записывается в виде x○y
Это не значит, что не используются другие формы записи бинарных операций. Существуют и другие виды записи:
· префиксная — x○y;
· постфиксная — xy○.
n-арным (n-местным) отношением на множестве A называется подмножество n-ой декартовой степени An множества A.
Число n для n-арной операции f (n-арного отношения r) называется арностью операции f (отношения r) и обозначается n(f) (n(r)).
Арности отношений – это числа большие нуля.
Арности операций – это числа большие или равные нулю. Операции арности 0 представляют собой функции с областью определения, состоящей из одного элемента (n-ки длины 0) и отождествляются со значением функции
13. -Понятие набора. Понятие «значения функции на данном наборе».
Методика построения таблиц истинности логических функций.
Логической (булевой) функцией (или просто функцией) n переменных y = f(x1, x2, …, xn) называется такая функция, у которой все переменные и сама функция могут принимать только два значения: 0 и 1.
Из определения логической функции следует, что функция п переменных – это отображение Еп в Е,которое можно задать непосредственно таблицей, называемой таблицей истинности данной функции. Например, функция трех переменных f(x,y,z) может определяться следующей таблицей истинности.
| x | y | z | f(x,y,z) |
Это означает, что f (0,0,0) = 1, f (0,0,1) = 0, f (0,1,0) = 1 и т. д.
Понятие дизъюнктивной нормальной формы (ДНФ).
Формула D называется дизъюнктивной нормальной формой (ДНФ), если она является дизъюнкцией элементарных конъюнкций, т.е. имеет вид D=K1 v K2 v …Kr, где каждая формула
Kj (j =1,...,r) - это элементарная конъюнкция. D называется совершенной ДНФ, если в каждую из ее конъюнкций Kj входят все n переменных из X
Элементарной конъюнкцией называется конъюнкция переменных высказываний и (или) их отрицаний.
Элементарной дизъюнкцией называется дизъюнкция переменных высказываний и (или) их отрицаний.






