 Если
Если  =
=  в линии имеют место только падающие волны.
в линии имеют место только падающие волны.


Коэффициент бегущей волны – КБ =  ;
;
Коэффициент отражения по напряжению – pU =  ;
;

Поиск: Рекомендуем:  Почему я выбрал профессую экономиста
Почему я выбрал профессую экономиста
 Почему одни успешнее, чем другие
Почему одни успешнее, чем другие
 Периферийные устройства ЭВМ Периферийные устройства ЭВМ
 Нейроглия (или проще глия, глиальные клетки) Нейроглия (или проще глия, глиальные клетки)
Категории:
|
Режим бегущих волн в линии без потерь
Коэффициент бегущей волны – КБ = Коэффициент отражения по напряжению – pU =
|
29.Режим смешанных волн в линии без потерь.
 При При  ≠ ≠  нагрузке линии сопротивлением, не равным волновому, в линии наблюдаются смешанные волны. Чем больше разница между сопротивлением нагрузки нагрузке линии сопротивлением, не равным волновому, в линии наблюдаются смешанные волны. Чем больше разница между сопротивлением нагрузки  и волновым сопротивлением и волновым сопротивлением  , тем больше разница между напряжением в пучности( , тем больше разница между напряжением в пучности( ) и во впадине( ) и во впадине( ). Коэффициент стоячей волны KC = ). Коэффициент стоячей волны KC =  = =  = =  = =  . .
|
40. Синтез реактивных двухполюсников по первой канонической схеме Фостера.
 Пусть задана реактансная функция вида Пусть задана реактансная функция вида  . Её можно разложить на сумму простых дробей, используя теорию вычетов: . Её можно разложить на сумму простых дробей, используя теорию вычетов:  , где , где   , ,  - вычеты функции - вычеты функции  (при них дробь обращается в бесконечность); m – число пар сопряжённых полюсов при p = ± jwK. Эти коэффициенты рассчитываются по формулам: (при них дробь обращается в бесконечность); m – число пар сопряжённых полюсов при p = ± jwK. Эти коэффициенты рассчитываются по формулам:  ; ;  ; ;  . Позже слагаемое . Позже слагаемое  можно будет рассматривать как операторное сопротивление индуктивности. В схеме двухполюсника ему соответствует последовательно включенная индуктивность можно будет рассматривать как операторное сопротивление индуктивности. В схеме двухполюсника ему соответствует последовательно включенная индуктивность 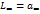 . Слагаемое . Слагаемое  можно рассматривать как операторное сопротивление ёмкости, ей соответствует последовательно включенная емкость можно рассматривать как операторное сопротивление ёмкости, ей соответствует последовательно включенная емкость  . Слагаемое . Слагаемое  соответствует паре мнимых полюсов функции соответствует паре мнимых полюсов функции  при p = ± jwk и его представим в виде при p = ± jwk и его представим в виде  и это параллельно соединённая ёмкость и это параллельно соединённая ёмкость  и индуктивность и индуктивность 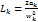 . Таким образом, . Таким образом,  . Такой записи соответствует схема: . Такой записи соответствует схема:
|
38. Общая характеристика задачи синтеза.
Задачей синтеза электрических цепей является нахождение схемы цепи и параметров входящих в неё элементов по заданным характеристикам цепи. Заданными характеристиками могут быть: операторные входные или передаточные функции (заданы аналитически); амплитудно-частотная или фазочастотная характеристика либо обе эти характеристики одновременно; переходная или импульсная характеристика (все – аналитически или в виде графиков). Передаточная функция – отношение изображения по Лапласу выходной величины к изображению по Лапласу входной величины.
K(p) =  ;
Например для дифференцирующей цепи:
K(p) = ;
Например для дифференцирующей цепи:
K(p) =  .
Задача синтеза имеет неоднозначное решение (может не иметь решений – когда получаются отрицательныеr, L, C). 1-ый этап решения – анализирование задачи (есть ли физическая реализуемость). 2-ой этап решения – расчёт параметров и структуры цепи, пользуясь одним из методов синтеза. Входные функции цепи и их свойства
I(p) = .
Задача синтеза имеет неоднозначное решение (может не иметь решений – когда получаются отрицательныеr, L, C). 1-ый этап решения – анализирование задачи (есть ли физическая реализуемость). 2-ой этап решения – расчёт параметров и структуры цепи, пользуясь одним из методов синтеза. Входные функции цепи и их свойства
I(p) =  ; Z(p), Y(p) – входная функция. ; Z(p), Y(p) – входная функция.
   p = s + jw; если p = s, то Z(p) и Y(p) – вещественные положительные функции. Z(p) = p = s + jw; если p = s, то Z(p) и Y(p) – вещественные положительные функции. Z(p) =  , где , где  – нули функции, – нули функции,  полюса функции. Нули и полюса находятся в левой полуплоскости комплексной плоскости. По их расположению можно судить о свойствах электрической цепи. Если все полюсы на отр. вещ. полуоси – переходный процесс носит характер периодический. Если полюсы в левой компл. полуплоскости, то переходный процесс носит характер затухающих колеб., чем ближе они расположены к мнимой оси, тем медленнее затухают эти колебания. полюса функции. Нули и полюса находятся в левой полуплоскости комплексной плоскости. По их расположению можно судить о свойствах электрической цепи. Если все полюсы на отр. вещ. полуоси – переходный процесс носит характер периодический. Если полюсы в левой компл. полуплоскости, то переходный процесс носит характер затухающих колеб., чем ближе они расположены к мнимой оси, тем медленнее затухают эти колебания.
|
41. Синтез реактивных двухполюсников по второй канонической схеме Фостера.
Пусть операторная проводимость имеет вид:  . Учитывая, что это выражение по характеру совпадает с выражением для . Учитывая, что это выражение по характеру совпадает с выражением для  , можно записать: , можно записать:  , где первое слагаемое , где первое слагаемое  , второе – операторная проводимость индуктивности , второе – операторная проводимость индуктивности  , а третье слагаемое , а третье слагаемое  . Представим . Представим  . Это слагаемое можно рассматривать как операторную проводимость последовательного контура, состоящего из индуктивности . Это слагаемое можно рассматривать как операторную проводимость последовательного контура, состоящего из индуктивности  и ёмкости и ёмкости  . Таким образом, . Таким образом,  . Такой записи соответствует схема: . Такой записи соответствует схема:

|
42. Синтез реактивных двухполюсников по первой цепной схеме Кауэра.
Метод Кауэра основан на представлении двухполюсника в виде 1-ой и 2-ой цепной схемы, в зависимости от того, при каких p реактансная функция имеет полюс (при p→∞ или при p = 0). Индуктивность и ёмкость 1-ой и 2-ой цепной схем получаются путём последовательного деления из входных функций Z(p) и Y(p) на Aip и  соответственно. Если полюс при p→∞:
Пусть ZВХ = A1p + Z1(p). Тогда Y1(p) = A2p + Y2(p). Тогда Z2(p) = A3p + Z3(p) и т. д. соответственно. Если полюс при p→∞:
Пусть ZВХ = A1p + Z1(p). Тогда Y1(p) = A2p + Y2(p). Тогда Z2(p) = A3p + Z3(p) и т. д.
 Можно записать Можно записать  . Данной цепной дроби соответствует 1-ый рисунок. . Данной цепной дроби соответствует 1-ый рисунок.
     Если Z(p) имеет нуль при p→∞, то раскладывают на цепные дроби функцию Y(p): Пусть ZВХ = Если Z(p) имеет нуль при p→∞, то раскладывают на цепные дроби функцию Y(p): Пусть ZВХ =  + Z1(p). Тогда YВХ(p) = + Z1(p). Тогда YВХ(p) = 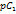 + Y1(p). Тогда Z2(p) = + Y1(p). Тогда Z2(p) =  + Z3(p) и т. д. Можно записать + Z3(p) и т. д. Можно записать  . Данной дроби соответствует 2-ой рисунок. . Данной дроби соответствует 2-ой рисунок.
|
43. Синтез реактивных двухполюсников по второй цепной схеме Кауэра.
Если реактансная функция имеет полюс при p = 0, мы должны получить цепную дробь следующего вида:  . Если реактансная функция имеет нуль при p = 0, то раскладывают на цепные дроби функцию Y(p). Рассмотрим пример: реализовать цепной схемой реактивный двухполюсник: . Если реактансная функция имеет нуль при p = 0, то раскладывают на цепные дроби функцию Y(p). Рассмотрим пример: реализовать цепной схемой реактивный двухполюсник:  . Произведём деление:
Искомая дробь: . Произведём деление:
Искомая дробь: 
  Искомая схема: Искомая схема:


|
45. Эквивалентные преобразования цепей с нелинейными элементами.
Цепь является нелинейной, если содержит хотя бы один нелинейный элемент (НЭ). Для ЛЭ  ; способы задания ВАХ: графический, табличный и аналитический.
Задаются током и суммируют амплитуды I (послед. соед.)
Задаются напряжением и суммируют амплитуды U (паралл. соед.)
Как сделать линейной нелинейную характеристику?
Статическая линеаризация: На 2-ом графике НЭ можно заменить на ; способы задания ВАХ: графический, табличный и аналитический.
Задаются током и суммируют амплитуды I (послед. соед.)
Задаются напряжением и суммируют амплитуды U (паралл. соед.)
Как сделать линейной нелинейную характеристику?
Статическая линеаризация: На 2-ом графике НЭ можно заменить на


  Е находится из графика. Е находится из графика.
  
|
46. Расчёт нелинейной цепи с одним нелинейным элементом.
 Пусть дана цепь:
1-ый способ: по заданным ВАХ ЛЭ и НЭ найти результирующую:
задать несколько точек для ЛЭ (по принципу U = IR) и просуммировать с ВАХ НЭ. Таким образом находится U(I).
2-ой способ: построить ВАХ ЛЭ, зеркально отобразить её относительно оси I, сместить её на величину Е и найти току пересечения полученной прямой с ВАХ НЭ. Координаты этой точки UНЭ и I и будут решениями системы. Пусть дана цепь:
1-ый способ: по заданным ВАХ ЛЭ и НЭ найти результирующую:
задать несколько точек для ЛЭ (по принципу U = IR) и просуммировать с ВАХ НЭ. Таким образом находится U(I).
2-ой способ: построить ВАХ ЛЭ, зеркально отобразить её относительно оси I, сместить её на величину Е и найти току пересечения полученной прямой с ВАХ НЭ. Координаты этой точки UНЭ и I и будут решениями системы.
 
|
47. Расчёт нелинейной цепи методом эквивалентного генератора.
Расчёт нелинейной цепи методом эквивалентного генератора применяется в случае, когда в цепи имеется только один НЭ. Для этого нужно всю цепь представить в виде активного двухполюсника.

     Представив схему в виде суммы двух составляющих, заметим, что в первой из них ток равен нулю (при любом сопротивлении НЭ, т.к. UНЭ = 0), а во второй ток будет таким же, как и в исходной схеме. Для нахождения ЕГ, исключают НЭ и находят напряжение на его зажимах. Для нахождения RГ вместо источников напряжения делают КЗ, вместо источников тока делают ХХ, и рассчитывают сопротивление. Далее составляют ВАХ RГ и находят решение так же, как и для цепи с одним нелинейным элементом. Представив схему в виде суммы двух составляющих, заметим, что в первой из них ток равен нулю (при любом сопротивлении НЭ, т.к. UНЭ = 0), а во второй ток будет таким же, как и в исходной схеме. Для нахождения ЕГ, исключают НЭ и находят напряжение на его зажимах. Для нахождения RГ вместо источников напряжения делают КЗ, вместо источников тока делают ХХ, и рассчитывают сопротивление. Далее составляют ВАХ RГ и находят решение так же, как и для цепи с одним нелинейным элементом.
    Пример: I1 = Пример: I1 = 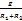 ; Uxx = Eг = I1R2 – I0R4. Rг = ; Uxx = Eг = I1R2 – I0R4. Rг =  . .
|
48. Расчёт нелинейной цепи методом двух узлов.
Метод двух узлов используется, если цепь содержит несколько параллельных ветвей и всего два узла. Исходную цепь преобразуют в цепь, где UЭ(I) получаются смещением характеристик каждой на свою величину ЭДС. На полученных графиках подбирают такое
  UАБ, при котором будет выполняться 1-ый закон Кирхгофа для узла. Токи I1, I2, I3 получаются при пересечении вертикальной прямой, проходящей через UАБ. UАБ, при котором будет выполняться 1-ый закон Кирхгофа для узла. Токи I1, I2, I3 получаются при пересечении вертикальной прямой, проходящей через UАБ.

|
49. Стабилизация напряжения с помощью НЭ.
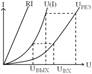
Стабилизация напряжения – явление, когда относительно большому приращению входного напряжения соответствует относительно малое приращение выходного напряжения.  . k = 10… 104. . k = 10… 104.  Другая схема стабилизации:
Другая схема стабилизации:

|
50. Устойчивость равновесия нелинейной цепи постоянного тока.
  Пусть дана цепь последовательного соединения индуктивности и НЭ. Уравнение для этой цепи: Пусть дана цепь последовательного соединения индуктивности и НЭ. Уравнение для этой цепи: 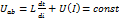 . .
 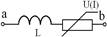 Если предположить, что РТ находится на участке 0 – 1 и предположить, что произошло кратковременное увеличение тока, то и UL также увеличится, но в силу UAB = const должно уменьшиться U(I), что приведёт к уменьшению тока I. Аналогичное явление характерно для РТ, находящейся на участке 2 – 3. Если РТ находится на участке 1 – 2, то случайное увеличение тока приводит к увеличению UL и уменьшению U(I), что влечёт за собой ещё большее увеличение тока. Если ток случайно уменьшить, то РТ перейдёт на участок 0 - 1→ не следует располагать РТ на участке 1 – 2. (i↗ → UL↗→ U(I)↘→i↗). Если предположить, что РТ находится на участке 0 – 1 и предположить, что произошло кратковременное увеличение тока, то и UL также увеличится, но в силу UAB = const должно уменьшиться U(I), что приведёт к уменьшению тока I. Аналогичное явление характерно для РТ, находящейся на участке 2 – 3. Если РТ находится на участке 1 – 2, то случайное увеличение тока приводит к увеличению UL и уменьшению U(I), что влечёт за собой ещё большее увеличение тока. Если ток случайно уменьшить, то РТ перейдёт на участок 0 - 1→ не следует располагать РТ на участке 1 – 2. (i↗ → UL↗→ U(I)↘→i↗).
|
51. Методы аппроксимации нелинейной ВАХ в цепи синусоидального тока.
Классификация НЭ: инерционные (типа лампочки), могут иметь линейную и нелинейную зависимость U(I) и I(U); безынерционные (типа диодов), могут иметь только нелинейную зависимость U(I) и I(U)l.
НЭ могут иметь симметричные и несимметричные ВАХ.
Инерционные элементы и их цепи при известном положении РТ на характеристике можно линеаризовать и считать комплексным(?) либо классическим методом.
Безынерционные цепи нужно рассчитывать учитывая, что при синусоидальном токе в цепи появляется несинусоидальное напряжение (или наоборот).
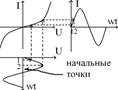 Есть целый ряд методов линеаризации (аппроксимации) НЭ.\
Аппроксимация степенным полиномом: i(u) = a0 + a1(u – u0) + a2(u – u0)2 + …
при u0 = 0: i(u) = a0 + a1u + a2u + … - всю ВАХ или её рабочую часть представляют конечным числом слагаемых ряда Тейлора, где u0 = напряжение в РТ ВАХ. Для нахождения коэффициентов аппроксимации ak решают уравнения (IВХ и UВХ известны). Пусть UВХ = UMsinwt, учитывая 0, 1, 2, 3 гармоники: Есть целый ряд методов линеаризации (аппроксимации) НЭ.\
Аппроксимация степенным полиномом: i(u) = a0 + a1(u – u0) + a2(u – u0)2 + …
при u0 = 0: i(u) = a0 + a1u + a2u + … - всю ВАХ или её рабочую часть представляют конечным числом слагаемых ряда Тейлора, где u0 = напряжение в РТ ВАХ. Для нахождения коэффициентов аппроксимации ak решают уравнения (IВХ и UВХ известны). Пусть UВХ = UMsinwt, учитывая 0, 1, 2, 3 гармоники:
 = =  = =  = =  .
Графическая аппроксимация (метод 3-х ординат): .
Графическая аппроксимация (метод 3-х ординат):
 Кусочно – линейная аппроксимация – график нелинейной зависимости заменяется ломаной линией.
e = E0 + EMsinwt. По ВАХ: Кусочно – линейная аппроксимация – график нелинейной зависимости заменяется ломаной линией.
e = E0 + EMsinwt. По ВАХ:  . .
    где где 
|
52. Эквивалентная линеаризация НЭ в цепи синусоидального тока.
Эквивалентная линеаризация НЭ применяется в случае, если высшими гармониками тока или напряжения можно пренебречь. Если есть НЭ R, L, C, то им в соответствие ставятся их линейные элементы по критериям: амплитуда 1-ой гармоники U НЭ = амплитуда U ЛЭ. Линеаризация может быть построена на принципе гармонического и энергетического балансов. Гармонический баланс – линейные R, L, C выбираются так, чтобы амплитуда их U была равна амплитуде 1-ой (основной) гармоники на соответствующем НЭ. Энергетический баланс – линейные R, L, C выбираются так, чтобы мощности на них и мощности, определяемые 1-ой (основной) гармоникой на соответствующем НЭ были одинаковыми. Независимо от принципа, R, L, C получаются одинаковыми.
Для резистора:
k = UMsinwt, u1 =  ; uR = RIM. Отсюда ; uR = RIM. Отсюда  RI1M.
R = RI1M.
R = 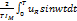 .
Через мощность: .
Через мощность:  , ,  , ,  , ,  . Мы вернулись к: . Мы вернулись к:  RI1M.
Для индуктивности: RI1M.
Для индуктивности:  ; ; 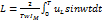 .
Для ёмкости: .
Для ёмкости:  ; ;  . .
|
|
|
|
|
|
Дата добавления: 2016-09-06; Мы поможем в написании ваших работ!; просмотров: 762 | Нарушение авторских прав
Лучшие изречения: