Узел, ветвь и МКТ через узлы и ветви эл.схемы
Узел – это точка соединения двух или нескольких ветвей. Узел, объединяющий две ветви называют устранимым, так как он находится внутри новой образованной ветви.
Ветвь – участок электрической цепи между двумя узлами, в котором все элементы соединены последовательно.
Узел, ветвь и МУН через узлы и ветви эл.схемы
3. Узел, ветвь и МТВ через узлы и ветви эл.схемы
Пассивные элементы.
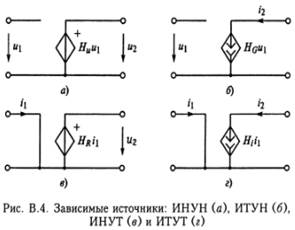
5,6.Изобразите схему зависимых источников ИНУН,ИТУТ. Какими св-ми они обладают?
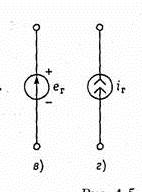
7.Какие идеальные независимые источники энергии вы знаете? Их условное изображения и св-ва
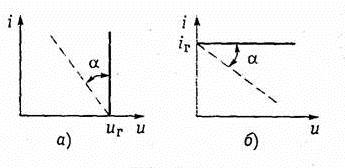
Идеальные источник энергии: источник напряжения –источник, у которого u(t) на зажимах не зависит от величины тока. условное обозначение под в),стрелка указывает направление электродвижущей силы. Источник тока идеализированный элемент, ток которого не зависит от напряжения на его зажимах. Условное обозначение источника тока показано на рис. 1.5, г. ВАХ для в)и г)
Закон Кирхгофа.
Алгебраическая сумма токов ветвей, сходящихся в любом узле эл. цепи, равна 0.
Закон Кирхгофа.
Алгебраическая сумма напряжений ветвей в любом замкнутом контуре равна 0.
10. Что называется идеальной индуктивностью?
Индуктивным элементом называют идеализированный элемент эл. схемы, обладающий только свойством накопления им энергии магнитного поля.
11. Что называется идеальной емкостью?
Емкостным элементом называется идеализированный элемент эл. цепи, обладающий только свойством накапливать энергию эл. поля.
12.Чему равно индуктивное сопротивление?
13.Чему равно емкостное сопротивление?
Ый закон Кирхгофа в сим. форме
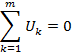
Ый закон Кирхгофа в сим. форме
Комплексные сопротивления
Смотри 19!
17.Представление гармонической функции вращающимся вектором. Почему при построении векторных диаграмм положение одного из векторов можно выбирать произвольно?
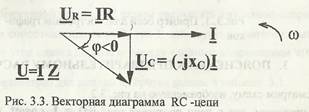
При построении векторных диаграмм нужно точно соблюдать углы сдвига фаз между векторами, а положение осей координат можно выбрать произвольно
Комплексная амплитуда.
Комплексная амплитуда - комплексная величина модуль и аргумент которого соответственно равны амплитуде и начальной фазе гармонического воздействия.
i(t)=Imsin(2πft+ϕ)
Im =Imejϕ комплексная амплитуда тока
Iд = Im / 
комплексное действующее значение
Найдите комплексное Z (с чертой) и общее реактивное сопротивление схем, содержащих пассивные элементы R,L и C
Z =R+jX=R+j(xl-xc)
Сформулируйте теорему об эквивалентном источнике напряжения.
Любой активный двухполюсник его воздействие на цепь можно заменить эквивалентной схемой, составленной из последовательного соединения идеального источника напряжения с ЭДС равно напряжению холостого хода активного двухполюсника и внутреннему сопротивлению тела, относительно разомкнутого зажима.
Дуальность.
Принцип дуальности: если для данной электрической цепи справедливы некоторые законы,
уравнения или соотношения, то они будут справедливы и для дуальных величин в дуальной цепи.
Приведем дуальные понятия:
1. Напряжение и ток (u и i)
2. Сопротивление и проводимость (R и G)
3. Индуктивность и ёмкость (L и C)
4. I и II законы Кирхгофа
5. Последовательное и параллельное соединения
Ток в любой ветви ЛЭЦ не изменится, если активный двухполюсник, к которому подключена данная ветвь, заменить эквивалентным источником напряжения (ЭДС) с напряжением (ЭДС), равным напряжению холостого хода
