Пусть две индуктивно связанные катушки с параметрами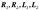 
и М соединены параллельно. Согласное соединение получается при подключении к одному и тому же узлу одноименных зажимов, встречное - разноименных.Первый случай отмечен на схеме звездочками, второй - точками.
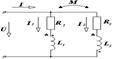
Параллельное соединение индуктивно связанных элементов
(21) методы расчета разветвленных индуктивно связанных цепей
Для расчета разветвленных цепей с индуктивно связанными элементами (рис. 9.8) используем метод контурных токов.
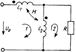
Рис. 9.8
Контурные уравнения в комплексной форме имеют общий вид:
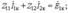
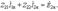
Выбор независимых контуров указан стрелками на схеме.
При записи собственных и общих сопротивлений запишем по уже известным правилам сначала члены, не связанные с взаимной индуктивностью. Далее учтем члены, отражающие индуктивные связи. В собственных сопротивлениях контуров слагаемые + j2ωM появляются, если обе индуктивно связанные катушки входят в данный контур и их маркировка соответствует согласному включению в этом контуре. Если при обходе контура, включающего две связанные катушки, одна из катушек обтекается контурным током в положительном, а другая – в отрицательном направлении, то член в соответствующем собственном сопротивлении будет иметь знак “минус”, т. е. – j2ωM.
При записи общего сопротивления двух контуров учитывается их взаимное индуктивное влияние друг на друга. Здесь член jωM имеет знак “плюс”, если положительные направления обоих контурных токов ориентированы одинаково относительно маркированных зажимов катушек, и оба тока протекают по ним либо в положительном, либо в отрицательном направлении. Если же один из влияющих друг на друга токов протекает в положительном, а другой – в отрицательном направлении, в общем сопротивлении контуров учитывают член – jωM. С учетом сформулированных правил получим для контурных сопротивлений цепи (см. рис. 9.8):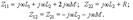 
(22) явление резонанса
Явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротность.
Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником. Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно, так и параллельно. При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения
,
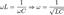где ω = 2πf; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы.
(23) Резонанс напряжений
Резонанс напряжений - резонанс, происходящий в последовательном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает с собственной частотой контура.
Если в цепь переменного тока включены последовательно катушка индуктивности и конденсатор, то они по-своему воздействуют на генератор, питающий цепь, и на фазовые соотношения между током и напряжением. Катушка индуктивности вносит сдвиг фаз, при котором ток отстает от напряжения на четверть периода, конденсатор же, наоборот, заставляет напряжение в цепи отставать по фазе от тока на четверть периода. Если величина емкостного сопротивления цепи больше индуктивного, то цепь носит емкостный характер, т. е. напряжение отстает по фазе от тока. Если же, наоборот, индуктивное сопротивление цепи больше емкостного, то напряжение опережает ток, и, следовательно, цепь носит индуктивный характер. Общее реактивное сопротивление Хобщ рассматриваемой нами цепи определяется путем сложения индуктивного сопротивления катушки XL и емкостного сопротивления конденсатора ХС.
Но так как действие этих сопротивлений в цепи противоположно, то одному из них, а именно Хс приписывается знак минус, и общее реактивное сопротивление определяется по формуле:
Хобщ = XL -ХС, XL = ωL, ХС = 1 / ωС
Применив к этой цепи закон Ома, получим:
I = U / Хобщ
общее сопротивление цепи определяется следующей формулой:
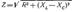
где R — общее активное сопротивление цепи, XL -ХС — ее общее реактивное сопротивление. Индуктивное и емкостное сопротивления, соединенные последовательно, вызывают в цепи переменного тока меньший сдвиг фаз между током и напряжением, чем если бы они были включены в цепь по отдельности.
Одновременно с этим действующие напряжения как на катушке UL = IXL так и на конденсаторе Uc = IХС окажутся равными и будут максимально большой величины. При малом активном сопротивлении цепи эти напряжения могут во много раз превысить общее напряжение U на зажимах цепи. Это интересное явление называется в электротехнике резонансом напряжений.
При резонансе напряжений мощность источника тока будет затрачиваться только на преодоление активного сопротивления цепи, т. е. на нагрев проводников.
цепь переменного тока, состоящая из генератора и последовательно соединенных катушки индуктивности и конденсатора, при определенных условиях XL = ХС превращается в колебательную систему. Такая цепь получила название колебательного контура.
Частота генератора
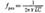Значение емкости и индуктивности цепи, при которых наступает резонанс напряжений:
Lрез = 1 / ω2С, Срез = 1 / ω2L
Изменяя любую из этих трех величин (fрез, L и С), можно вызвать в цепи резонанс напряжений, т. е. превратить цепь в колебательный контур.
(24) частотные характеристики последовательного контура
Последовательный колебательный контур. Последовательный колебательный контур образуется при последовательном соединении катушки индуктивности и конденсатора. Эквивалентная схема рис.3.7 для анализа цепи включает и омическое сопротивление R, при помощи которого учитываются потери в реальной индуктивности и емкости.
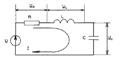
Частотные характеристики и полоса пропускания последовательного колебательного контура. Зависимости сопротивлений и сдвига фазы между током и напряжением от частоты называются частотными и фазовыми характеристиками контура и определяются формулами:
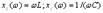
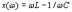
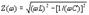
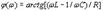
Графики зависимости xL(ω), хC(ω), х(ω) и Z(ω) изображены на рис.3.8.а, а зависимости φ(ω) –на рис.З.8.б.
(25) резонанс токов
Резонансом токов называется такой режим в электрической цепи, содержащей катушку индуктивности и конденсатор, при котором токи на этих элементах равны, но противоположны по фазе. При резонансе проводимости индуктивности и конденсатора (bL = bC) равны. При резонансе ток и напряжение на входе цепи совпадают по фазе.
В параллельном контуре реактивная составляющая тока замкнута в контуре и к ней прибавляется активная составляющая тока, получаемая от источника. Чтобы рассчитать величины этих составляющих тока, вводится понятие реактивной и активной проводимости цепи. Только по индуктивности протекает реактивная и активная составляющая тока (см. рис.1), для расчета этих составляющих, мы вводим эквивалентную замену катушки (см. рис.2).
Реактивную составляющую тока (IL.p), проводимость индуктивности (bL) и активную составляющую тока (IR.a), проводимость активного сопротивления катушки (g), рассчитываем по формулам:
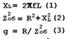
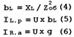
При резонансе тока, ток в контуре зависит от напряжения подаваемого на него и от его реактивной проводимости. Ток источника (Ia), подаваемый на контур, зависит от его активной проводимости.
При резонансе токов активный ток (потребляемый от источника) очень мал, а реактивный ток "замкнутый" в контуре достаточно большой.
При очень низком Rакт., контур фактически отсоединяется от нагрузки.
Снизив количество витков в катушке до 70 -50 витков, мы можем получить реактивный ток 100 - 200 мА, при очень малом токе потребления от нагрузки!
(26) частотные характеристики параллельного контура
Параллельный колебательный контур. Параллельный колебательный контур образуется при параллельном соединении катушки индуктивности и конденсатора с генератором тока (рис.3.10). Действительные сопротивления R1 и R2 введены в схему для отображения соответственно потерь энергии в катушке индуктивности и конденсаторе.
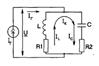
Частотные характеристики параллельного контура без потерь определяются зависимостью параметров его элементов от частоты и имеют вид: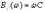 
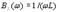
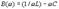
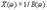
(27) периодические несинусоидальные воздействия
Искажение ЭДС и токов может возникать вследствие конструктивных особенностей генераторов переменного тока, приводящих к тому, что создаваемая ими ЭДС несинусоидальна, либо вследствие нелинейности элементов электрической цепи. Причем для появления искажений достаточно наличия в цепи только одного нелинейного элемента. Чаще всего обе эти причины присутствуют одновременно, но в зависимости от степени выраженности их воздействия на цепь пренебрегают одной из них или обеими сразу.
Из курса математики известно, что любую несинусоидальную периодическую функцию F(w t) удовлетворяющую условиям Дирихле, т.е. имеющую за полный период конечное число максимумов, минимумов и разрывов первого рода, можно представить в виде ряда Фурье
F(wt) = A0 + A1sin(wt+y 1) + A2sin(2wt+y 2) +ј + Aksin(kwt+y k)+ј =
A0 + B1sinwt + B2sin2wt +ј + Bksinkwt+ј
ј + C1coswt + C2cos2wt +ј + Ckcoskwt +ј =
A0+a1+a2+ј + ak+ј,
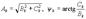
где.
Первый член ряда A0 называется постоянной составляющей или нулевой гармоникой. Второй член A1sin(wt+y 1) имеет частоту равную частоте функции F(wt) и называется первой или основной гармонической составляющей (коротко - гармоникой). Остальные члены ряда вида Aksin(kwt+y k) имеют частоты в целое число раз k больше частоты основной гармоники и называются высшими гармоническим составляющими или гармониками. Каждая высшая гармоника в отдельности именуется по номеру k, т.е. вторая гармоника, третья гармоника и т.д.
(28) расчет цепей при периодических несинусоидальных воздействиях
Если в линейной электрической цепи действует один или
несколько источников несинусоидальных периодических ЭДС и токов, то расчет такой цепи ведется в три этапа.
1. Разложение ЭДС и/или задающего тока источника в тригонометрический ряд Фурье.
2. Расчет токов и напряжений для каждой гармоники.
2.1. Для постоянной составляющей цепь преобразуется с учетом того, что XL (0) = 0, XC (0) = ¥, и рассчитывается одним из методов постоянного тока.
2.2. Для основной (первой) гармоники символическим методом (метод контурных токов, метод узловых потенциалов, метод эквивалентного генератора, метод наложения) рассчитываются необходимые токи и напряжения.
2.3. Для высших гармоник определяются параметры цепи по формулам (2.28) и (2.29) и при использовании того же метода расчета, что и в 2.2, рассчитываются токи и напряжения.
3. Совместное рассмотрение решений для каждой гармоники.
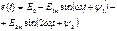
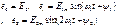
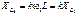
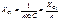
1. Электрическая цепь и элементы электрической цепи.
2. Законы Ома и Кирхгофа.
3.Принцип наложения.
4.Метод контурных токов.
5.Метод узловых потенциалов.
6. Метод эквивалентного генератора.
7. Баланс мощности.
8.Расчет электрической цепи с зависимыми источниками.
9.Гармонические токи, напряжения, ЭДС.
10. Способы представления гармонических колебаний.
11.Гармонические колебания в резистивных, индуктивных и емкостных элементах.
12.Гармонические колебания в цепи при последовательном соединении R,L,C элементов.
13. Гармонические колебания в цепи при параллельном соединении R,L,C элементов.
14. Символический метод расчета цепей в разветвленных электрических цепях.
15.Мощности в цепях синусоидального тока.
16.Баланс мощностей в цепях при гармонических воздействиях.
17.Топографические и векторные диаграммы.
18. Комплексные входные и передаточные характеристики электрических цепей.
19.Явление взаимной индукции. ЭДС и напряжение взаимной индукции.
20.Последовательное и параллельное соединения индуктивно связанных элементов.
21.Методы расчета разветвленных индуктивно связанных цепей.
22.Явление резонанса.
23.Резонанс напряжений.
24.Частотные характеристики последовательного колебательного контура.
25.Резонанс токов.
26.Частотные характеристики параллельного колебательного контура.
27.Периодические несинусоидальные воздействия.
28. Расчет цепей при периодических несинусоидальных воздействиях.
